聚类 - 5 - 谱和谱聚类

         本总结是是个人为防止遗忘而作，不得转载和商用。

 

谱

         什么是谱？

         先说说咱们口头上经常说的“某个人靠不靠谱”，一般，如果一个人遵守行为准则（即：此人言而有信、说到做到），那这个人就靠谱，反正这个人就不靠谱。

         反映到坐标轴上的话，如果这条线代表行为准则：

         如果一个人的行为不会偏离行为准则很多，那就说这个人“靠谱”，如下图：

                  

         反之，如果一个人的行为总偏离行为准则很多，那就说这个人“不靠谱”，如下图：

        

         最后对应到机器学习的中，谱的定义就是：

                   方阵作为线性算子，它的所有特征值的全体统称方阵的谱；

                   方阵的谱半径为最大的特征值；

                   矩阵A的谱半径：(A^TA)的最大特征值。

         其实，这里谱的本质是伪逆，是SVD中奇异值的平方。

谱聚类

         谱聚类是一种基于图论的聚类方法，通过对样本数据的拉普拉斯矩阵的特征向量进行聚类，从而达到对样本数据聚类的目的。

谱分析的思想

         1，给定一组数据x 1 ,x2 ,...x n ，记任意两个点之间的相似度(―距离”的减函数)为s ij <xi,xj>，形成相似度图(similarity graph)：G=(V,E) 。如果x i 和x j 之间的相似度s ij 大于一定的阈值，那么，两个点是连接的，权值记做s ij。

                   总之这一步就是得出一个n*n的邻接矩阵，方阵中的每个元素sij代表第i个元素和第j个元素之间的相似度

         2，接下来，可以用相似度图来解决样本数据的聚类问题：找到图的一个划分，形成若干个组(Group)，使得不同组之间有较低的权值，组内有较高的权值。

若干概念

         在上面思想的基础上，我们来整理一些概念。

                  无向图：G(V, E)

                   邻接矩阵（是对称阵）：

                            W = (w_ij)，i,j = 1, 2, ..., n

                            其中w_ij表示第i个元素和第j个元素之间的相似度(相似度的计算见“聚类 -1 - 聚类介绍”)。然后规定自己和自己的相似度为0(自己和自己的相似度当然是最大的，所以不用管)，即w_ii = 0，即：

                            邻接矩阵的主对角线都是0。

                            又因为“第i个元素和第j个元素之间的相似度” = “第j个元素和第i个元素之间的相似度”，即w_ij= w_ji，所以：

                            邻接矩阵对称。

                   第i个样本的度：

                           

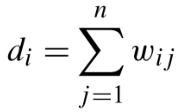
                            即：第i个样本和其他所有样本的相似度的和。

                   度矩阵（是对角阵）：

                            求出第i个样本的度之后，将其写到一个n*n的矩阵的对角线上，该矩阵的其他元素都是0，如下：

                                     d1   0 ...  0

                                      0  d2...  0

                                      0 ... 0  .  0

                                      0 ... 0 ......dn

                            这个矩阵就是度矩阵。

                   拉普拉斯矩阵（是对称阵）：

                            未正则的拉普拉斯矩阵：L= 度矩阵(D) - 邻接矩阵(W)

                            正则的拉普拉斯矩阵    

                                     对称拉普拉斯矩阵         ：Lsym = D^-(1/2)·L·D^(1/2)= I - D^-(1/2)·W·D^(1/2)           

                                     随机游走拉普拉斯矩阵：L_rw= D^-1L = I - D^-1W

                            PS：因为D是对角阵，所以D^-(1/2)只需要把D的对角线上的元素开根后取倒数就好。

谱聚类算法：未正则拉普拉斯矩阵

         输入：n个点{p i }，簇的数目k

         步骤：

                   1，计算n×n的相似度矩阵W和度矩阵D；

                   2，计算拉普拉斯矩阵L=D-W；

                            PS：L=D-W是计算前k小的特征向量，如果是L=W-D则是计算前k大。

                   3，计算L的前k个特征向量（特征值对应的特征向量）u1 ,u2 ,...,uk ；

                            PS：如果L是个n*n的矩阵，那u1就是有n个元素的向量，uk同理。

                   4，将k个列向量u1 ,u2,...,uk 组成矩阵U，U∈R^n×k ；

                            PS：U是个n行k列的矩阵，第一行就是表征原始第一号样本，只不过原始第一号样本有n个值，而这里是用k个值表征的原始第一号样本（和SVD的原理有些像 -- 这句话看不懂那建议你看看我总结的SVD），其他行同理。

                   5，对于i=1,2,...,n,令y i ∈R^k是U的第i行的向量；

                   6，使用k-means算法将点(y i )i=1,2,...,n 聚类成簇C1 ,C2 ,...Ck ；即：在第四步的解释中已经说明：U的每一行就是一个样本，那就把这一个个样本代入K-means中聚类就好。

                   7，输出簇A1 ,A2,...Ak ，其中，Ai={j|y_j∈C_i}

谱聚类算法：对称拉普拉斯矩阵

         1，把“谱聚类算法：未正则拉普拉斯矩阵”第二步的L=D-W改成L= D^-(1/2)·(D-W)·D^(1/2)         2，在把“谱聚类算法：未正则拉普拉斯矩阵”的第五步和第六步之间添加一步：对于i=1,2,...,n,将y i ∈R k 依次单位化，使得|y i |=1；

         其他都一样。

谱聚类算法：随机游走拉普拉斯矩阵

         把“谱聚类算法：未正则拉普拉斯矩阵”第二步的L=D-W改成L=D^-1(D-W)，其他都一样。