归并排序

在归并排序的迭代算法中，可以把输入序列看成是个n个已排序序列，其中每个序列的长度为1，将这些序列两两归并就得到了 n/2个长度为2的序列（如果n为奇数，则有一个序列长度为1），然后对这n/2这个序列进行两两归并，依次类推，直到只剩下一个序列为止。
归并排序是在输入记录上执行若干遍归并，其中第一遍归并的是长度为1的子序列，第二遍归并的是长度为2的子序列，而第i遍归并的是长度为$2^{i-1}$的子序列，因此，总的归并遍数为[$log_2$n]，由函数merge可知，可以在线性时间内归并两个已排序序列，这就意味着每遍归并的时间开销为O(n)，由于总共要归并[$log_2$n]遍，所以总的计算时间是O($nlogn$).
设输入序列为(26,5,77,1,61,11,59,15,48,19)，则归并过程为：

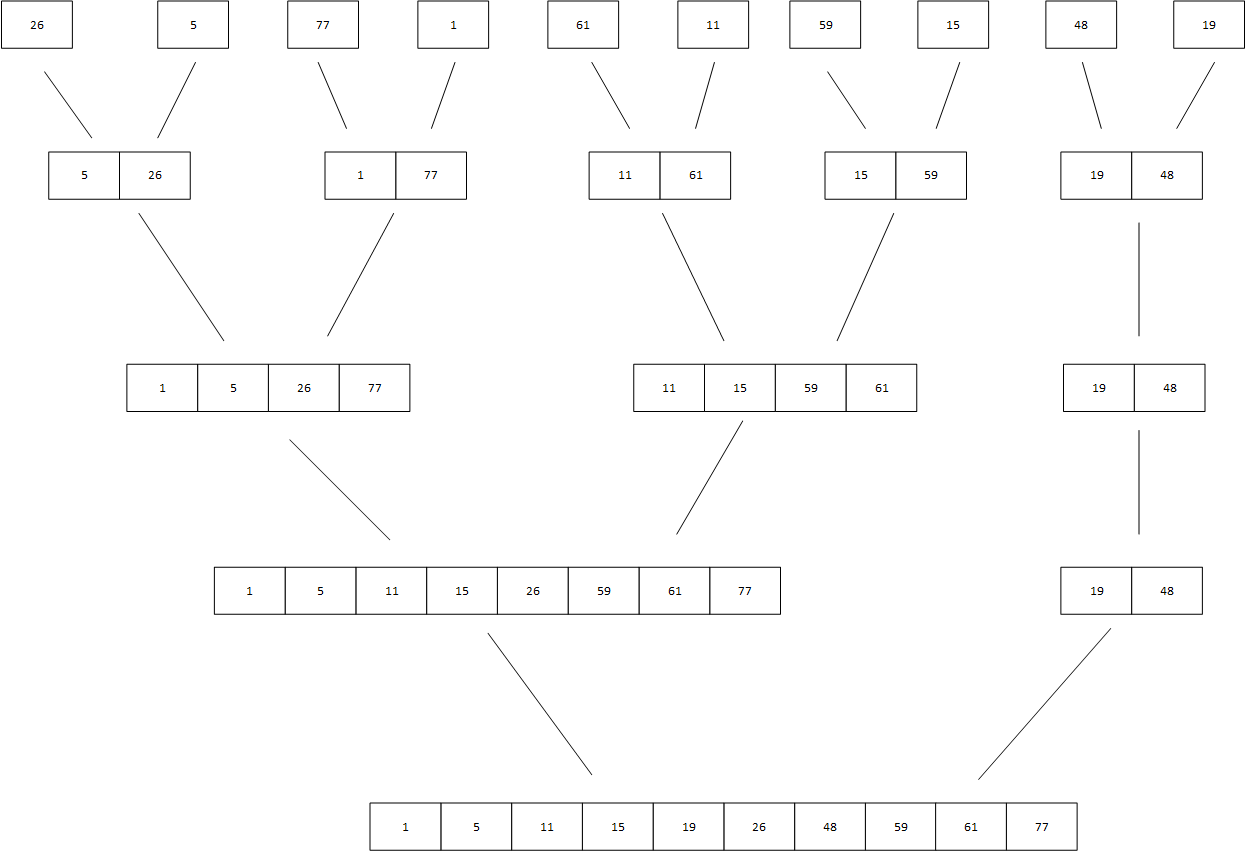
代码实现：

#include <iostream>
#include<stdio.h>
#include<algorithm>
#define MAX_SIZE 100
typedef struct
{
   int key;
}element;
element list[MAX_SIZE];

using namespace std;
//归并排序函数
void merge(element list[],element sorted[],int i,int m,int n)
{
   int j,k,t;
   //后半部分的起始索引
   j=m+1;
   // 前半部分的起始索引
   k=i;
   while(i<=m&&j<=n)
   {
      if(list[i].key<=list[i].key)
         sorted[k++]=list[i++];
      else
         sorted[k++]=list[j++];
   }
   if(i>m)
       //加入剩余的后半部分
      for(t=j;t<=n;t++)
         sorted[k+t-j]=list[t];
   else
      //加入剩余的前半部分
      for(t=i;t<=m;t++)
         sorted[k+t-i]=list[t];
}
//单遍归并的函数
void merge_pass(element list[],element sorted[],int n,int length)
{
   int i,j;
   //以length长度为一组，每两组又排序合并为一组
   for(i=0;i<=n-2*length;i+=2*length)
      merge(list,sorted,i,i+length-1,i+2*length-1);
      //判断最后是否只有一组还是两组
   if(i+length<n)
      //合并最后两组
      merge(list,sorted,i,i+length-1,n-1);
   else
   //加入剩下的最后一组
      for(j=i;j<n;j++)
         sorted[j]=list[j];
}
//分组排序归并
void merge_sort(element list[],int n)
{
   int length=1;
   element extra[MAX_SIZE];
   while(length<n)
   {
      merge_pass(list,extra,n,length);
      length*=2;
      merge_pass(extra,list,n,length);
      length*=2;
   }
}