CTF密码学之侧信道攻击出题思路

攻防_SRC

已于 2024-06-07 10:05:08 修改

阅读量2.7k

点赞数 70

文章标签：网络安全密码学

于 2024-06-07 10:04:24 首次发布

本文链接：https://blog.csdn.net/xuruihan177/article/details/139519433

版权

1.概要

本题目旨在测试参赛者对侧信道分析（Side-Channel Analysis）的理解和应用。参赛者需要通过分析能量轨迹数据，恢复被隐藏的明文信息（flag）。手册将涵盖相关概念解析、数学公式推导和解题思路说明。

2.侧信道攻击

2.1.侧信道攻击:

侧信道攻击是一种利用计算设备在执行加密操作时无意间泄露的物理信息来推断密钥或其他敏感数据的攻击方法。常见的侧信道包括功耗、时间、电磁辐射和声波等。

2.2.能量分析:

能量分析是侧信道攻击的一种，通过测量设备在加密操作过程中的功耗变化，来推断加密密钥或敏感数据。能量分析通常分为简单能量分析（Simple Power Analysis, SPA）和差分能量分析（Differential Power Analysis, DPA）。

2.3.模板攻击:

模板攻击是一种高效的侧信道攻击，攻击者事先构建设备在不同操作下的能量轨迹模板，通过对比实际操作中的能量轨迹与模板的相似度，来推断密钥或敏感数据。

2.4.能量轨迹

能量轨迹是指设备在执行加密操作时消耗的功率随时间变化的记录。通过分析能量轨迹，可以推测出设备在不同时间点上执行的操作，从而恢复加密数据。

3.侧信道攻击分类：

3.1.简单能量分析（SPA）:

SPA是通过观察单次加密操作的功耗曲线，来直接推断设备的内部状态。SPA需要攻击者具有一定的设备内部知识，以便通过观察功耗曲线的特征来推断出敏感信息。

3.2.差分能量分析（DPA）:

DPA通过多次加密操作的功耗曲线，结合统计分析方法来推断敏感信息。DPA通常对单次功耗测量中的噪声更为鲁棒，通过对多次测量结果进行差分分析，可以揭示出隐藏在噪声中的信息。

3.3.相关能量分析（CPA）:

CPA是DPA的一种变种，通过计算实际测量的功耗轨迹与假设功耗模型之间的相关性，来推断出密钥信息。CPA通常需要攻击者对目标设备的功耗模型有较好的了解。

3.4.模板攻击（TA）:

模板攻击需要攻击者事先在与目标设备相同的设备上，构建出针对不同输入和内部状态的功耗轨迹模板。在实际攻击过程中，通过比较测量到的功耗轨迹与模板之间的相似度，来推断出密钥信息。模板攻击通常被认为是最强的侧信道攻击之一，因为它利用了预先构建的详细模型。

4.数学公式推导

4.1.欧几里得距离

欧几里得距离是计算两个点之间的直线距离的数学公式。在本题中，用于比较不同能量轨迹之间的相似度。公式如下：
$d(\mathbf{x}, \mathbf{y}) = \sqrt{\sum_{i=1}^{n} (x_i - y_i)^2}$

4.2.能量轨迹匹配

假设有两个模板轨迹 $\mathbf{T}_0$ 和 $\mathbf{T}_1$ ,对应于比特值 0 和 1。给定一个目标轨迹 $\mathbf{T}$ ,通过计算 $\mathbf{T}$ 与 $\mathbf{T}_0$ $\mathbf{T}_1$ 的欧几里得距离来决定 $T$ 更接近于哪个模板，从而恢复比特值。

$d(\mathbf{T}, \mathbf{T}_0) = \sqrt{\sum_{i=1}^{n} (T_i - T_{0i})^2}$

$d(\mathbf{T}, \mathbf{T}_1) = \sqrt{\sum_{i=1}^{n} (T_i - T_{1i})^2}$

如果 $d(\mathbf{T}, \mathbf{T}_0) < d(\mathbf{T}, \mathbf{T}_1)$ ，
则该比特为0，否则为1。

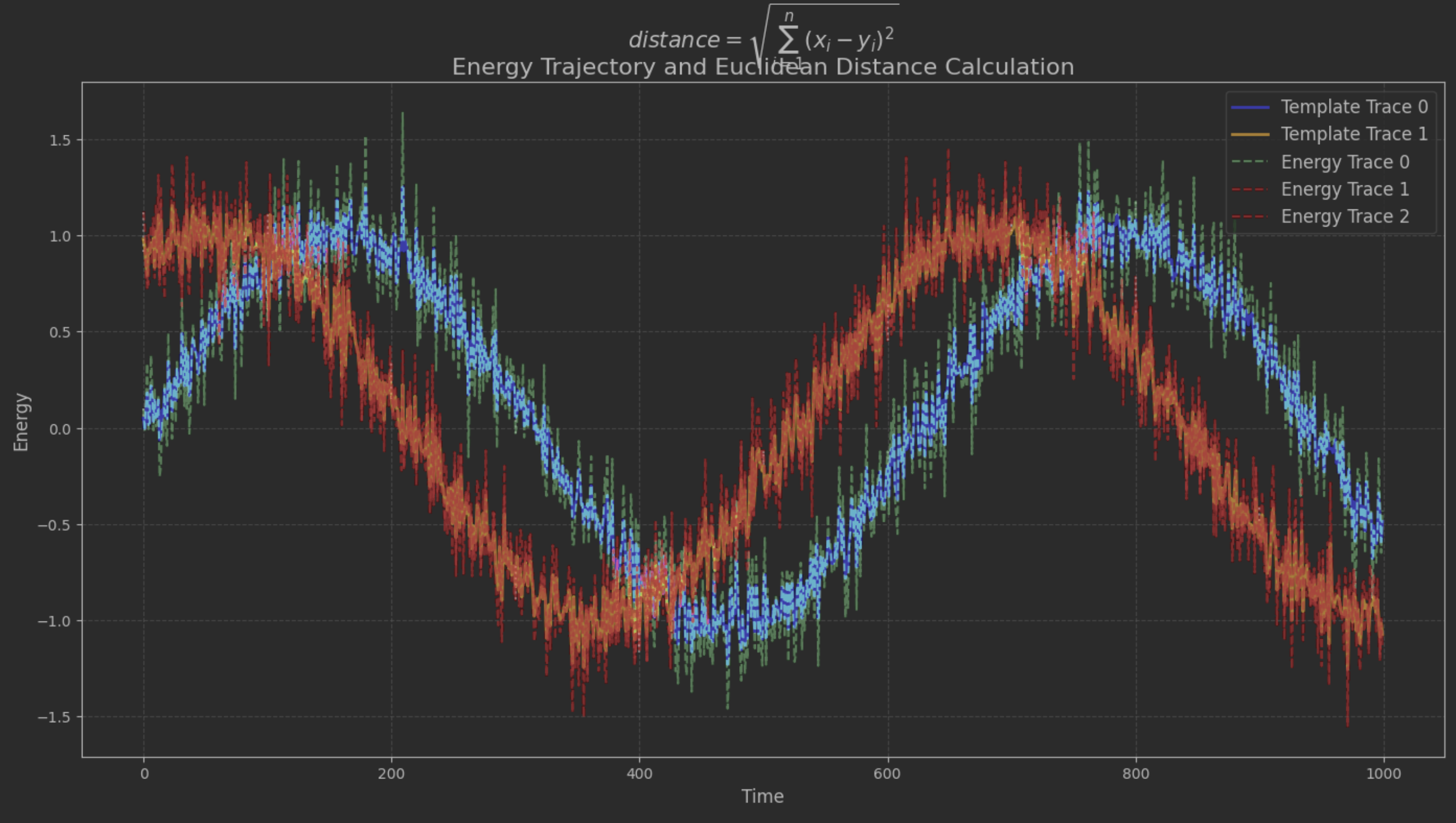
5.出题思路

5.1.生成模板轨迹：

生成两个模板轨迹 $\mathbf{T}_0$ 和 $\mathbf{T}_1$ ,分别对应比特值 0 和 1。使用随机噪声生成模板轨迹。

5.2.插入明文信息：

将明文信息（flag）转换为二进制位串。
根据每个位的值选择对应的模板轨迹，并加入随机噪声生成目标能量轨迹。

5.3.生成能量轨迹文件和图：

保存生成的能量轨迹到文件，并绘制能量轨迹图。

6.解题思路

6.1.加载能量轨迹文件和模板轨迹：

参赛者加载提供的能量轨迹文件和模板轨迹文件。

6.2.恢复比特值：

对每个能量轨迹计算其与模板轨迹 $\mathbf{T}_0$ 和 $\mathbf{T}_1$ 的欧几里得距离，恢复比特值。

6.3.转换为明文信息：

将恢复的二进制位串转换为明文信息。

7.题目信息

题目名称：能量追踪

7.1.技术背景

在实际操作中，每当设备执行加密运算时，其功耗会发生微小的变化。这些变化虽然细微，但通过精密的仪器可以记录下来。侧信道攻击利用了这些功耗变化，通过分析和对比，逐步还原出加密过程中使用的密钥或明文信息。图片为flag加密过程中不同阶段的能量消耗情况

7.2.参赛者拿到的代码

import numpy as np

# 加载模板轨迹文件
template_trace_0 = np.load('template_trace_0.npy')
template_trace_1 = np.load('template_trace_1.npy')

# 加载能量轨迹文件
traces = np.load('energy_traces_with_flag.npy')
def bits_to_text(bits):
    chars = [bits[i:i+8] for i in range(0, len(bits), 8)]
    text = ''.join([chr(int(char, 2)) for char in chars])
    return text
# 提示：参赛者需要推导如何从能量轨迹恢复二进制位，再将二进制位转换回明文 flag
# 题目包含附件总共5个
1.energy_traces_with_flag.npy
2.energy_traces_with_flag.png
3.template_trace_0.npy
4.template_trace_1.npy

8.解题思路：

题目通过侧信道攻击的方法来恢复加密的明文信息。

8.1.步骤1：理解能量轨迹和模板轨迹

能量轨迹是设备在处理数据时功耗变化的记录。在本题中，能量轨迹中嵌入了flag的二进制表示。模板轨迹是对能量轨迹的特定值（0或1）进行采样，形成的参考模型。

模板轨迹0 (template_trace_0): 代表二进制位为0时的能量轨迹。

模板轨迹1 (template_trace_1): 代表二进制位为1时的能量轨迹。

8.2.步骤2：加载能量轨迹文件和模板轨迹文件

加载已提供的能量轨迹文件和模板轨迹文件。可以使用 numpy 库来完成。

import numpy as np
import matplotlib.pyplot as plt

# 加载 .npy 文件
file_path1 = 'template_trace_0.npy'
file_path2 = 'template_trace_1.npy'
file_path3 = 'energy_traces_with_flag.npy'

template_trace_0 = np.load(file_path1)
template_trace_1 = np.load(file_path2)
energy_traces_with_flag = np.load(file_path3)

# 查看数据的基本统计信息
print("Template Trace 0: mean =", np.mean(template_trace_0), ", std =", np.std(template_trace_0))
print("Template Trace 1: mean =", np.mean(template_trace_1), ", std =", np.std(template_trace_1))
print("Energy Traces with Flag shape =", energy_traces_with_flag.shape)

# 选择更强的下采样因子
downsample_factor = 1

# 下采样数据
template_trace_0 = template_trace_0[::downsample_factor]
template_trace_1 = template_trace_1[::downsample_factor]
energy_traces_with_flag = energy_traces_with_flag[:, ::downsample_factor]

# 绘制能量轨迹图
plt.figure(figsize=(12, 6))
plt.plot(template_trace_0, label='template_trace_0', color='blue', linestyle='-')
plt.plot(template_trace_1, label='template_trace_1', color='orange', linestyle='--')

for i, trace in enumerate(energy_traces_with_flag[:10]):
    plt.plot(trace, linestyle='-.', label=f'energy_trace_with_flag_{i}')

plt.xlabel('Time')
plt.ylabel('Energy')
plt.title('Energy Trajectory Over Time')
plt.legend()
plt.grid(True)
plt.show()

模板轨迹 (template_trace_0 和 template_trace_1)：

template_trace_0（蓝色实线）：这是一个基准轨迹，显示了能量随时间的变化模式。

template_trace_1（橙色虚线）：这是另一个基准轨迹，显示了能量随时间的另一种变化模式。

插入了 flag 信息的能量轨迹 (energy_trace_with_flag_0 到 energy_trace_with_flag_9)：

这些轨迹是基于 template_trace_0 或 template_trace_1 加上随机噪声生成的，每个轨迹对应于 flag 字符串中的一个比特位（0或1）。

这些轨迹中，每个轨迹在总体趋势上跟随某一个模板轨迹，并在其基础上添加了随机噪声。

解读轨迹：

如果某个 energy_trace_with_flag 轨迹的总体趋势更接近 template_trace_0，那么这个轨迹可能对应于 flag 比特位中的 0。

如果某个 energy_trace_with_flag 轨迹的总体趋势更接近 template_trace_1，那么这个轨迹可能对应于 flag 比特位中的 1。

匹配模板：可以看到，大部分 energy_trace_with_flag 轨迹在某些时间段内与 template_trace_0 或 template_trace_1 有相似的趋势。这意味着这些轨迹是基于相应的模板轨迹生成的。

噪声影响：由于每个轨迹都添加了随机噪声，因此轨迹之间会有一些差异，但整体趋势仍能区分出是基于哪个模板生成的。

8.2.1.进一步的分析

为了更清晰地展示这种关系，可以尝试：

计算轨迹之间的相似度：通过计算每个 energy_trace_with_flag 轨迹与两个模板轨迹之间的相似度（例如均方误差），来确定其更接近哪个模板。

使用不同颜色区分：如果有大量的轨迹，可以对每个轨迹进行聚类分析，以便更好地区分不同类型的轨迹。

计算均方误差：定义一个 mse 函数，计算每个轨迹与模板轨迹之间的误差。

选择颜色：根据每个轨迹更接近的模板轨迹，选择不同的颜色绘制轨迹

import numpy as np
import matplotlib.pyplot as plt

# 加载 .npy 文件
file_path1 = 'template_trace_0.npy'
file_path2 = 'template_trace_1.npy'
file_path3 = 'energy_traces_with_flag.npy'

template_trace_0 = np.load(file_path1)
template_trace_1 = np.load(file_path2)
energy_traces_with_flag = np.load(file_path3)

# 计算均方误差
def mse(trace1, trace2):
    return np.mean((trace1 - trace2) ** 2)

errors_to_0 = [mse(trace, template_trace_0) for trace in energy_traces_with_flag]
errors_to_1 = [mse(trace, template_trace_1) for trace in energy_traces_with_flag]

# 打印误差以供参考
print("Errors to template_trace_0:", errors_to_0)
print("Errors to template_trace_1:", errors_to_1)

# 绘制能量轨迹图
plt.figure(figsize=(12, 6))
plt.plot(template_trace_0, label='template_trace_0', color='blue', linestyle='-')
plt.plot(template_trace_1, label='template_trace_1', color='orange', linestyle='--')

for i, trace in enumerate(energy_traces_with_flag[:10]):
    label = f'flag_{i}'
    color = 'green' if errors_to_0[i] < errors_to_1[i] else 'red'
    plt.plot(trace, linestyle='-.', label=label, color=color)

plt.xlabel('Time')
plt.ylabel('Energy')
plt.title('Energy Trajectory Over Time')
plt.legend()
plt.grid(True)
plt.show()

模板轨迹：

template_trace_0（蓝色实线）：基准轨迹之一，显示了能量随时间的变化模式。

template_trace_1（橙色虚线）：基准轨迹之二，显示了能量随时间的另一种变化模式。

带有 flag 信息的轨迹：

绿色轨迹：这些轨迹与 template_trace_0 的均方误差较小，因此可以认为这些轨迹对应的 flag 比特位是 0。

红色轨迹：这些轨迹与 template_trace_1 的均方误差较小，因此可以认为这些轨迹对应的 flag 比特位是 1。

8.3.步骤3：定义欧几里得距离公式

欧几里得距离公式用于计算两个向量之间的距离。

8.4.步骤4：通过模板匹配恢复明文的二进制形式

对于每一个能量轨迹，我们计算其与模板轨迹0和模板轨迹1之间的欧几里得距离。然后，选择距离较小的那个模板轨迹，判断该能量轨迹对应的二进制位是0还是1。

8.5.步骤5：运行恢复私钥的函数

调用 recover_private_key 函数，恢复出私钥（明文的二进制形式）。

8.6.步骤6：将恢复的二进制形式转换为明文

将恢复的二进制形式的私钥转换为明文信息。每8个二进制位代表一个字符。

import numpy as np
from scipy.spatial.distance import euclidean

# 加载能量轨迹文件
traces = np.load('energy_traces_with_flag.npy')

# 加载模板轨迹文件
template_trace_0 = np.load('template_trace_0.npy')
template_trace_1 = np.load('template_trace_1.npy')

# 恢复私钥（明文 flag 的二进制形式）
def recover_private_key(traces, template_trace_0, template_trace_1):
    private_key = []
    for trace in traces:
        # 计算轨迹与两个模板轨迹的欧几里得距离
        dist_0 = euclidean(trace, template_trace_0)
        dist_1 = euclidean(trace, template_trace_1)
        # 选择距离较小的模板轨迹对应的比特位
        private_key.append(0 if dist_0 < dist_1 else 1)
    return private_key

# 将恢复的二进制形式转换为明文 flag
def bits_to_text(bits):
    chars = [bits[i:i+8] for i in range(0, len(bits), 8)]
    text = ''.join([chr(int(char, 2)) for char in chars])
    return text

# 恢复私钥并转换为明文
private_key = recover_private_key(traces, template_trace_0, template_trace_1)
recovered_bits_str = ''.join(map(str, private_key))
recovered_plaintext = bits_to_text(recovered_bits_str)

print(f"Recovered plaintext: {recovered_plaintext}")

9.代码解释

代码使用了基于欧几里得距离的最近邻分类原理来恢复插入在能量轨迹中的 flag 信息。

9.1.数据加载

代码首先加载了插入 flag 信息的能量轨迹文件以及两个模板轨迹文件：

traces = np.load('energy_traces_with_flag.npy')
template_trace_0 = np.load('template_trace_0.npy')
template_trace_1 = np.load('template_trace_1.npy')

9.2.最近邻分类原理

对于每一个能量轨迹，代码计算它与两个模板轨迹的欧几里得距离。欧几里得距离用于度量两个向量之间的直线距离。公式为：
$\text{distance} = \sqrt{\sum_{i=1}^n (x_i - y_i)^2}$
其中 $x$ 和 $y$ 是两个向量，在代码中，对于每个能量轨迹 trace：

dist_0 = euclidean(trace, template_trace_0)
dist_1 = euclidean(trace, template_trace_1)

分别计算了 trace 与 template_trace_0 及 trace 与 template_trace_1 的欧几里得距离。

9.3.分类决定

代码通过比较两个距离，判断哪个模板轨迹与当前能量轨迹更接近：

private_key.append(0 if dist_0 < dist_1 else 1)

如果 trace 与 template_trace_0 的距离更小，则认为该能量轨迹对应的比特位为 0。

如果 trace 与 template_trace_1 的距离更小，则认为该能量轨迹对应的比特位为 1。

这部分代码利用了最近邻分类器的基本思想，即根据待分类样本与已知样本之间的距离来决定其类别。

9.4.恢复私钥

通过遍历所有能量轨迹，得到一个二进制比特位的列表 private_key，表示恢复的 flag 信息：

private_key = recover_private_key(traces, template_trace_0, template_trace_1)

9.5.将二进制比特位转换为明文

代码将恢复的二进制比特位转换为字符串，再将每8位二进制字符串转换为一个字符，最终组合成完整的明文 flag：

def bits_to_text(bits):
    chars = [bits[i:i+8] for i in range(0, len(bits), 8)]
    text = ''.join([chr(int(char, 2)) for char in chars])
    return text

9.6.打印恢复的明文

最终，代码打印恢复出的 flag：

recovered_plaintext = bits_to_text(recovered_bits_str)
print(f"Recovered plaintext: {recovered_plaintext}")

这种方法利用了模板轨迹的特征，通过比较距离来有效地恢复插入在能量轨迹中的隐藏信息。

10.引用

● 1.Kocher, Paul C., Joshua Jaffe, and Benjamin Jun. “Differential power analysis.” Advances in Cryptology—CRYPTO’99 (1999): 388-397.
https://link.springer.com/content/pdf/10.1007/3-540-48405-1.pdf

● 2.Brier, Eric, Christophe Clavier, and Francis Olivier. “Correlation power analysis with a leakage model.” International workshop on cryptographic hardware and embedded systems. Springer, Berlin, Heidelberg, 2004.
https://link.springer.com/content/pdf/10.1007/b99451.pdf

● 3.Mangard, Stefan, Elisabeth Oswald, and Thomas Popp. “Power analysis attacks: Revealing the secrets of smart cards.” Vol. 31. Springer Science & Business Media, 2008.
https://link.springer.com/content/pdf/10.1007/978-0-387-38162-6.pdf