分层图最短路是指在可以进行分层图的图上解决最短路问题。分层图:可以理解为有多个平行的图。
一般模型是:在一个正常的图上可以进行 k 次决策,对于每次决策,不影响图的结构,只影响目前的状态或代价。一般将决策前的状态和决策后的状态之间连接一条权值为决策代价的边,表示付出该代价后就可以转换状态了。
一般有两种方法解决分层图最短路问题:
- 建图时直接建成k+1层。
- 多开一维记录机会信息。
我们建k+1层图。然后有边的两个点,多建一条到下一层边权为0的单向边,如果走了这条边就表示用了一次机会。
有N个点时,1~n表示第一层,(1+n)~(n+n)代表第二层,(1+2*n)~(n+2*n)代表第三层,(1+i*n)~(n+i*n)代表第i+1层。因为要建K+1层图,数组要开到n * ( k + 1),点的个数也为n * ( k + 1 )
#pragma GCC optimize(3,"Ofast","inline")
#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<bits/stdc++.h>
using namespace std;
#define endl '\n'
typedef long long ll;
#define int long long
#define ld long double
int qd,zd;
const int N=5000100;
const int INF=999999999;
int cnt,head[N];
int dist[N],vis[N];
int n,m,k;
struct edge
{
int to,nx,w;
};
edge ed[2*N];
struct node{
int dist,id;
};
bool operator<(node z,node y){
return z.dist>y.dist;
}
void dijk(int s){
priority_queue<node>q;
q.push({0,s});
dist[s]=0;
while(q.size()){
auto k=q.top();
q.pop();
int id=k.id,dis=k.dist;
if(vis[id]) continue;
vis[id]=1;
for(int i=head[id];i!=-1;i=ed[i].nx){
int j=ed[i].to;
int w=ed[i].w;
if(dist[j]>dis+w){
dist[j]=dis+w;
q.push({dist[j],j});
}
}
}
}
void add(int a,int b,int c)
{
ed[++cnt].to=b;
ed[cnt].w=c;
ed[cnt].nx=head[a];
head[a]=cnt;
}
void solve()
{
cin>>n>>m>>k;
cin>>qd>>zd;
int tn=n*k+n;
for(int i=0;i<=tn;i++) {head[i]=-1;
dist[i]=INF;vis[i]=0;}
for(int i=1;i<=m;i++){
int a,b,s;
cin>>a>>b>>s;
add(a,b,s);
add(b,a,s);
//一共有k条免费路径,则一共有k+1层
for(int j=1;j<=k;j++){
//第1+j层的路径
add(a+(j*n),b+(j*n),s);
add(b+(j*n),a+(j*n),s);
//下一层,与本层的链接
add(a+((j-1)*n),b+(j*n),0);
add(b+((j-1)*n),a+(j*n),0);
}
}
//k+1层,终点路径为0,答案直接输出最后一层
for(int i=1;i<=k;i++){
add(zd+(i-1)*n,zd+i*n,0);
}
dijk(qd);
cout<<dist[zd+k*n];
}
signed main()
{
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
solve();
return 0;
}https://ac.nowcoder.com/acm/contest/40326/B
二维图,建双层
#include<bits/stdc++.h>
using namespace std;
#define endl '\n'
typedef long long ll;
#define int long long
#define ld long double
const int N=220000;
int cnt,head[N];
int n,m,qi,zong;
int vis[N],dist[N];
const int INF=999999999;
struct edge
{
int to,nx,w;
};
edge ed[4*N];
void add(int a,int b,int c)
{
ed[++cnt].to=b;
ed[cnt].w=c;
ed[cnt].nx=head[a];
head[a]=cnt;
}
struct node{
int z,y,id;
}a[100010];
bool cmp1(node z,node y){
if(z.z==y.z) return z.y<y.y;
return z.z<y.z;
}
bool cmp2(node z,node y){
if(z.y==y.y) return z.z<y.z;
return z.y<y.y;
}
struct noe{
int id,sum;
};
bool operator<(noe z,noe y){
return z.sum>y.sum;
}
void dijk(){
priority_queue<noe>w;
dist[qi]=0;
w.push({qi,0});
while(w.size()){
auto k=w.top();
int id=k.id,sum=k.sum;
w.pop();
if(vis[id]) continue;
vis[id]=1;
for(int i=head[id];i!=-1;i=ed[i].nx){
int j=ed[i].to;
int tw=ed[i].w;
if(dist[j]>sum+tw){
dist[j]=sum+tw;
w.push({j,dist[j]});
}
}
}
}
void solve()
{ cnt=0;
cin>>n>>m;
n=(m+2)*2;//一共n个点,每一层m+2个点
int zm=m+2;
for(int i=1;i<=n;i++) {head[i]=-1;dist[i]=INF;}
for(int i=1;i<=zm;i++){
cin>>a[i].z>>a[i].y;
a[i].id=i;
}
sort(a+1,a+1+zm,cmp1);
for(int i=1;i<zm;i++){
//第一层,横向边
if(a[i].z==a[i+1].z){
int tz=a[i].id;
int ty=a[i+1].id;
int w=(a[i+1].y-a[i].y)*2;
add(tz,ty,w);
add(ty,tz,w);
}
}
sort(a+1,a+1+zm,cmp2);
for(int i=1;i<zm;i++){
//第二层,纵向边
if(a[i].y==a[i+1].y){
int tz=a[i].id+zm;
int ty=a[i+1].id+zm;
int w=(a[i+1].z-a[i].z)*2;
add(tz,ty,w);
add(ty,tz,w);
}
}
for(int i=1;i<=m;i++){
//前m个点可以改方向,从第一层转移到第二层
int tz=i;
int ty=i+zm;
add(tz,ty,1);//两层互相走为1
add(ty,tz,1);
}
qi=m+1,zong=m+2;//起点,终点
//return;
add(qi,qi+zm,0);//起点与第二层
add(zong,zong+zm,0);//终点与第二层
zong=zong+zm;//防止BUG,直接走到第二层终点
dijk();
if(dist[zong]==INF) dist[zong]=-1;
cout<<dist[zong];
}
signed main()
{
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
solve();
return 0;
}题目大意: 从一号点出发,到达的2-n的点,的路径中 min{路径之和--路径最长边+路径最短边},
相当于,最短边路径*2,最长边消失。
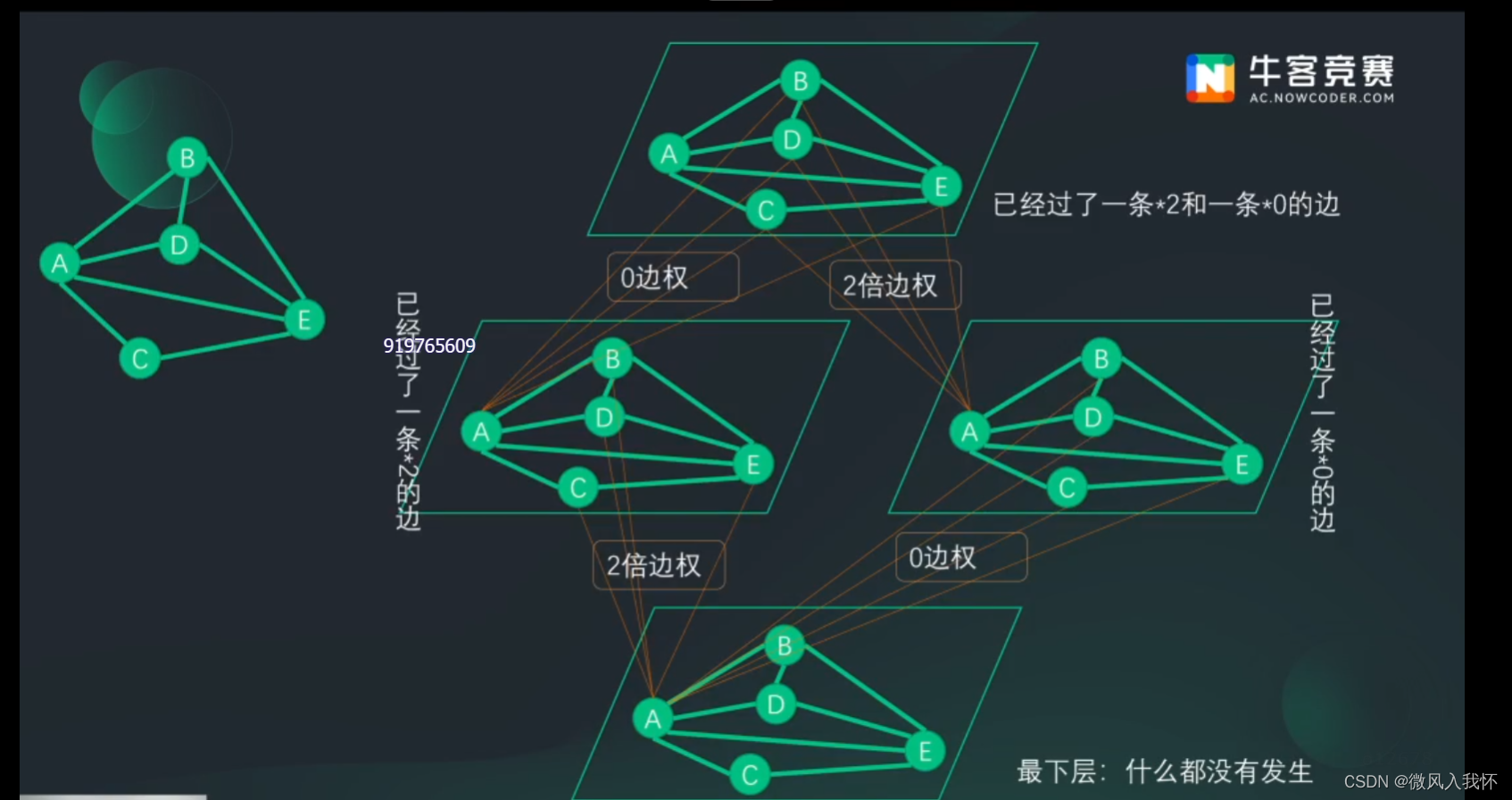
故可以使用分层图:
1-4层为这条边,既当最大也当最小
1-2-4为0,2
1-3-4为2,0
第一步分层即可优先找2倍距离,也可找0距离
建图后,直接跑dijk即可
#include<bits/stdc++.h>
using namespace std;
#define endl '\n'
typedef long long ll;
#define int long long
#define ld long double
const int N=800010;
int cnt,head[N];
int n,m,qi,zong;
int vis[N],dist[N];
const int INF=19999999999999999;
struct edge
{
int to,nx,w;
};
edge ed[N*3];
void add(int a,int b,int c)
{
ed[++cnt].to=b;
ed[cnt].w=c;
ed[cnt].nx=head[a];
head[a]=cnt;
}
struct noe{
int id,sum;
};
bool operator<(noe z,noe y){
return z.sum>y.sum;
}
void dijk(){
priority_queue<noe>w;
dist[1]=0;
w.push({1,0});
while(w.size()){
auto k=w.top();
int id=k.id,sum=k.sum;
w.pop();
if(vis[id]) continue;
vis[id]=1;
for(int i=head[id];i!=-1;i=ed[i].nx){
int j=ed[i].to;
int tw=ed[i].w;
if(dist[j]>sum+tw){
dist[j]=sum+tw;
w.push({j,dist[j]});
}
}
}
}
void ad(int a,int b,int c){
add(a,b,c);//第一层
add(a+n,b+n,c);//二
add(a+2*n,b+2*n,c);//三
add(a+3*n,b+3*n,c);//四
//1->2 2->4
add(a,b+n,0);
add(a+n,b+3*n,2*c);
//1->3 3->4
add(a,b+2*n,2*c);
add(a+2*n,b+3*n,0);
//1->4
add(a,b+3*n,c);
}
void solve()
{ cnt=0;
cin>>n>>m;
for(int i=1;i<=4*n;i++) {
head[i]=-1,dist[i]=INF;
}
for(int i=1;i<=m;i++){
int a,b,c;
cin>>a>>b>>c;
ad(a,b,c);
ad(b,a,c);
}
int num=0;
dijk();
for(int i=2;i<=n;i++){
num=dist[i+3*n];
cout<<num<<" ";
}
}
signed main()
{
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
solve();
return 0;
}方法1: tarjan
..图是一个有环图,因为是单向边,缩点,成有向无环图后,每一个强连通分量记录,内部最大值,最小值.
题目必须从1点出发,缩点后,建立新图,为拓扑图,无法从1到达的点全部删除;
从一点出发,进行拓扑操作,若a->b则,a的值可以更新b
输出终点值即可;
#include<bits/stdc++.h>
using namespace std;
#define endl '\n'
#define int long long
const int N=2000100;
const int INF=9999999999;
int cnt,head[N],n,m,timestamp;
int dfn[N];//时间戳
int low[N];
int stk[N],top,in_stk[N];//栈
int scc_cnt;//分量数
int Size[N];//强连通分量点的个数
int id[N];//强连通分量
int dout[N];//缩点后的出度
int din[N];//缩点后的入度
int c[N];
int maxv[N],minv[N];
struct edge
{
int to,nx;
};
edge ed[N*10];
void add(int a,int b)
{
ed[++cnt].to=b;
ed[cnt].nx=head[a];
head[a]=cnt;
}
void tarjan(int u){
dfn[u]=low[u]=++timestamp;
stk[++top]=u,in_stk[u]=true;
for(int i=head[u];i!=-1;i=ed[i].nx){
int j=ed[i].to;
if(!dfn[j]){
tarjan(j);
low[u]=min(low[u],low[j]);
}
else if(in_stk[j]){
low[u]=min(low[u],dfn[j]);
}
}
if(dfn[u]==low[u]){
int y=0;
++scc_cnt;//强连通分量总数+1
do{
y=stk[top--];//取栈顶元素y
maxv[scc_cnt]=max(maxv[scc_cnt],c[y]);
minv[scc_cnt]=min(minv[scc_cnt],c[y]);
in_stk[y]=false;//则y不再在栈中
id[y]=scc_cnt;//点y在此连通图
Size[scc_cnt]++;//第scc_cnt个连通块点数+1
}while(y!=u);
}
}
int ans[N];
void bfs(){
for(int i=1;i<=scc_cnt;i++){
maxv[i+n]=maxv[i];
minv[i+n]=minv[i];
head[n+i]=-1;
ans[n+i]=maxv[i]-minv[i];
}
//统计新图中点的出度
for(int i=1;i<=n;i++){//判断i到k是不是在一个分量中
for(int j=head[i];j!=-1;j=ed[j].nx){
int k=ed[j].to;
int a=id[i],b=id[k];
//a,b不为一个连通分量
if(a!=b) {
//缩点后的有向无环图,建立新图
//拓扑排序图
add(a+n,b+n);
din[b+n]++;}
//a出度+1 dout[a] += i→k
}
}
int s=n+id[1];//起点
queue<int>q;
//缩点后的有向无环图,无法从S到达的点全删除
for(int i = 1; i <= scc_cnt; i ++)
if(!din[n+i]&&n+i!=s)
q.push(n+i);
while(q.size())
{
int key = q.front();
q.pop();
for(int i = head[key]; i!=-1; i = ed[i].nx)
{
int j = ed[i].to;
din[j] --;
if(!din[j]) q.push(j);
}
}
q.push(s);//起点开始拓扑排序
while(q.size())
{
int key=q.front();//key后面的点可以更新
q.pop();
ans[key]=max(ans[key],maxv[key]-minv[key]);
for(int i = head[key]; i!=-1; i = ed[i].nx)
{
int j = ed[i].to;
//传递性
ans[j]=max(ans[j],ans[key]);
minv[j]=min(minv[j],minv[key]);
din[j] --;
if(!din[j]) q.push(j);
}
}
//必须到达终点
cout<<ans[n+id[n]];
}
void solve()
{ cnt=0;top=0;timestamp=0;cin>>n>>m;
for(int i=1;i<=n;i++) {
maxv[i]=-INF,minv[i]=INF;
head[i]=-1;dfn[i]=0;}
for(int i=1;i<=n;i++) cin>>c[i];
while(m--){
int a,b,c;cin>>a>>b>>c;
if(c==1)
add(a,b);//有向图
else{
add(a,b),add(b,a);
}
}
//缩点,把所有强连通分量缩成一个点
for(int i=1;i<=n;i++){
if(!dfn[i]){
tarjan(i);
}
}
bfs();//进行拓扑排序
}
signed main()
{
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
solve();
return 0;
}方法2;分层图,因为买一步,卖一步。那么建三层图,
1-->2层 买了一个
2->3层 卖出一个
终点就是在第三层,
因为需要最大值,因而走最长路,最长路可以使用最短路。
把全部边权变成负数,跑最短路,结果取负值就行。
边权为负数,因而使用spfa跑
#pragma GCC optimize(3,"Ofast","inline")
#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<bits/stdc++.h>
using namespace std;
#define endl '\n'
typedef long long ll;
#define int long long
#define ld long double
const int N=301000;
const int INF=999999999;
int dist[N];
bool st[N];
int cnt,head[N];
int n,m,c[N];
struct edge
{
int to,nx,w;
};
edge ed[N*10];
void add(int a,int b,int c)
{
ed[++cnt].to=b;
ed[cnt].w=c;
ed[cnt].nx=head[a];
head[a]=cnt;
}
void spfa(){
dist[1]=0;
queue<int>q;
q.push(1);
st[1]=1;
while (q.size())
{
int t = q.front();
q.pop();
st[t] = false;
for (int i = head[t]; i != -1; i = ed[i].nx)
{
int j = ed[i].to;
if (dist[j] > dist[t] + ed[i].w)
{
dist[j] = dist[t] + ed[i].w;
if (!st[j])//如果在队列就不需要
{
q.push(j);
st[j] = true; // 松弛后就 true
}
}
}
}
}
void solve()
{ cnt=0;
cin>>n>>m;
//走最长路的话,边权全为负值,结果加负号即可
for(int i=1;i<=3*n;i++) {
dist[i]=INF,st[i]=0,head[i]=-1;}
for(int i=1;i<=n;i++) cin>>c[i];
while(m--){
int a,b,s;
cin>>a>>b>>s;
add(a,a+n,c[a]);//买
add(a+n,a+2*n,-c[a]);//卖
add(b,b+n,c[b]);//买
add(b+n,b+2*n,-c[b]);//卖
if(s==1){
add(a,b,0);
add(a+n,b+n,0);
add(a+2*n,b+2*n,0);
}else{
add(a,b,0);
add(a+n,b+n,0);
add(a+2*n,b+2*n,0);
add(b,a,0);
add(b+n,a+n,0);
add(b+2*n,a+2*n,0);
}
}
spfa();
cout<<-dist[n+2*n];
}
signed main()
{
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
solve();
return 0;
}




















 735
735











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








