哈希表（闭散列、拉链法--哈希桶）

       哈希表，也称散列表，是一种通过key值来直接访问在内存中的存储的数据结构。它通过一个关键值的函数（被称为散列函数）将所需的数据映射到表中的位置来访问数据。

关于哈希表，主要为以下几个方面：

一、哈希表的几种方法

1、直接定址法：取关键字key的某个线性函数为散列地址，如Hash(key) = key  或 Hash(key) = A*key+B；A,B为常数

2、除留取余法：关键值除以比散列表长度小的素数所得的余数作为散列地址。Hash(key) = key % p;

3、平均取中法：先计算构成关键码的标识符的内码的平方，然后按照散列表的大小取中间的若干位作为散列地址。

4、折叠法：把关键码自左到右分为位数相等的几部分，每一部分的位数应与散列表地址位数相同，只有最后一部分的位数可以短一些。把这些部分的数据叠加起来，就可以得到具有关键码的记录的散列地址。分为移位法和分界法。

5、随机数法：选择一个随机函数，取关键字的随机函数作为它的哈希地址。

6、数学分析法：设有N个d位数，每一位可能有r种不同的符号。这r种不同的符号在各位上出现的频率不一定相同，可能在某些位上分布均匀些，每种符号出现的机会均等；在某些位上分布不均匀，只有某几种符号经常出现。可根据散列表的大小，选取其中各种符号分布均匀的若干位作为散列地址。

在这里，我们建哈希表的方法用除留取余法为例。

尽管有这么多种方法，但是不同的key值可能会映射到同一散列地址上。这样就会造成哈希冲突/哈希碰撞。

那么遇到哈希冲突我们该如何处理呢？

二、处理哈希冲突的闭散列方法

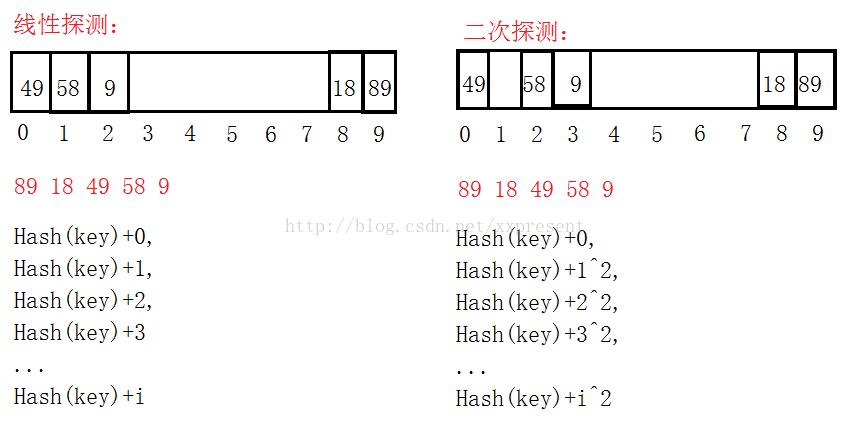
1、线性探测：当不同的key值通过哈希函数映射到同一散列地址上时，检测当前地址的下一个地址是否可以插入，如果可以的话，就存在当前位置的下一个地址，否则，继续向下一个地址寻找，地址++。

2、二次探测：是针对线性探测的一个改进，线性探测后插入的key值太集中，这样造成key值通过散列函数后还是无法正确的映射到地址上，太集中也会造成查找、删除时的效率低下。因此，通过二次探测的方法，取当前地址加上i^2，可以取到的新的地址就会稍微分散开。

如：此时的散列表长度为10：

看到以上的例子之后，我们只是存入int型的数据时，计算余数寻找地址是比较容易的。如果我们存入的是字典值（string类型），那么我们就要通过string类型来转化成数值来计算地址。这里用到了BKDR哈希算法（字符串哈希算法）。

同时，经研究表明，通过素数表作为哈希表的长度可以降低哈希冲突。

三、闭散列实现代码

主要实现如下：

#pragma once
#include<vector>
#include<iostream>
using namespace std;
#include<assert.h>
#include<string>

enum Status
{
	EXIST,
	DELETE,
	EMPTY
};

template<class K,class V>
struct HashTableNode
{
	K _key;
	V _value;
	Status _status;
	HashTableNode(const K&