【程序设计训练】作业训练二 18.棋盘（三种解法：分治、动规、DFS）

目录

题目

前言（可忽略）

方法一：分治

可行性

代码

反思

方法二：动态规划

分析与转化

代码

反思

方法三：DFS

分析

代码

反思

---

题目

【问题描述】

        棋盘是指一个行和列编号从1~N的NxN的二进制矩阵，当行号和列号之和为偶数时该矩阵对应位置为黑色的(1)，否则为白色的(0)。以下图示为N=1、2、3时的棋盘。

                

         給出一个NxN的二进制矩阵，请找出位于该矩阵内的最大尺寸的完整棋盘，以及最大尺寸棋盘的数量（棋盘可以交叠）。

【输入形式】

       每个测试用例的第一行是一个正整数N(1<=N<=2000)，表示給定矩阵的行数和列数，接下来的N行描述了这个矩阵：每行有N个字符，既可以是“1”（代表黑块），也可以是“0”（代表白块）。矩阵至少包含一个“1”字符。

【输出形式】

       输出最大尺寸棋盘的行列的大小，以及最大棋盘的个数，以空格分隔。

【样例输入】

5
00101
11010
00101
01010
11101

【样例输出】

3 3

【样例说明】
【评分标准】

前言（可忽略）

做了三天的训练题，个人感觉此题之前的题比起数据结构和算法的考察，更关注的确实是“程序设计”，应该大致是对应ccf-csp认证前两题题型的。

这道题和前面的题相比，风格明显不同。所以我乍一看以为处理方式有质的变化，就把简单的问题复杂化了。我写的第一个超时的分治方法，就是一个教训。因为分治的失败，所以才有了后面几种方法的思考和实现。虽然对于此题来说还是最简单直接的拓展方法在考试最优，但我也希望其他几种方法的研究能有助于选择合适高效的算法，以及衔接上认证测试后几道题的难度。

方法一：分治

可行性

1.显然，1x1二进制矩阵在该格为1时属于尺寸为1的棋盘。

2.每个NxN二进制矩阵（N>1）可以分解为4个(N-1)x(N-1)的相同问题。

3.这道题子问题不独立，有重叠的部分，也可以用分治做，但是效率很低，不如动态规划。这是我最开始在思考中忽略的一点，也有分治和动态规划都不是很熟练的原因。

4.显然成立。

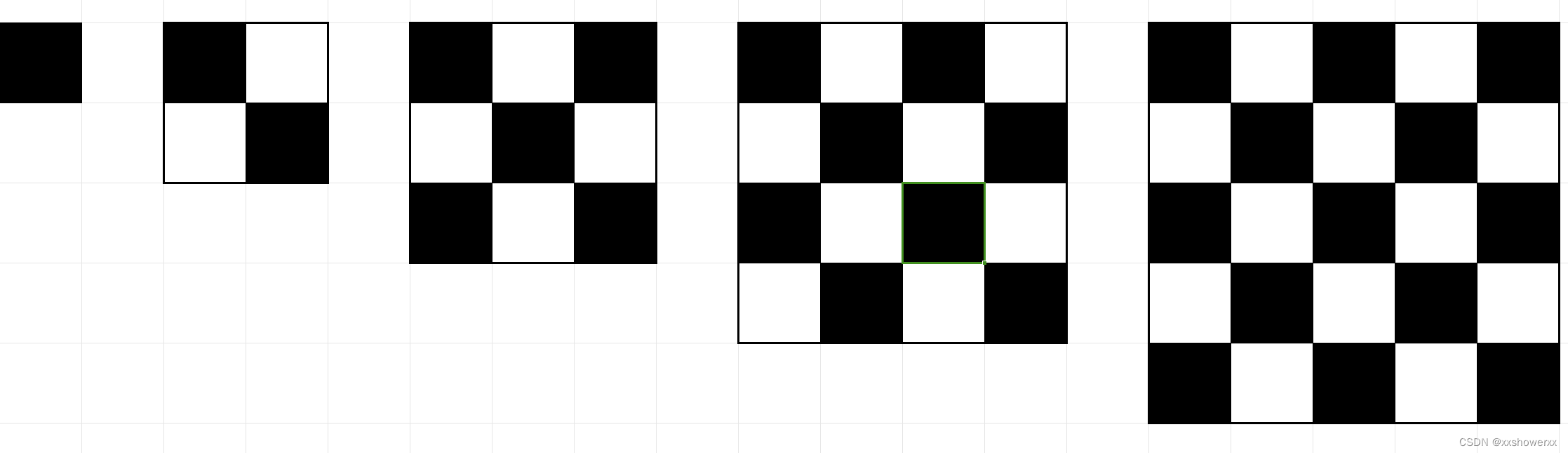
对应颜色边框代表小棋盘的范围。

N>1的二进制矩阵为棋盘的充要条件是包含如上图以红蓝为左上角格，N-1xN-1大小的两个小棋盘，以黄粉为为左上角格，N-1xN-1大小的两个取反小棋盘。

由此，二进制矩阵不止棋盘有意义，取反棋盘也有意义。且还存在第三种状态，既不属于棋盘又不属于取反棋盘。N=1时，格为1属于棋盘，格为0属于取反棋盘。

然后我们就容易得出下面代码递归的返回值和判断条件。

代码

#include<bits/stdc++.h>
using namespace std;
char a[2005][2005];
int mark[2005][2005];
int max_size=1;
int partition(int row,int col,int size) {
	if(size==1) {
		if(a[row][col]=='1') {
			if(size>mark[row][col])
				mark[row][col]=size;
			return 1;
		} else
			return -1;
	} else {
		int a=partition(row,col,size-1),b=partition(row+1,col,size-1),
		    c=partition(row,col+1,size-1),d=partition(row+1,col+1,size-1);
		if(a==1&&b==-1&&c==-1&&d==1) {
			if(size>=max_size)
			{
				max_size=size;
				mark[row][col]=size;
			}
			return 1;
		} else if(a==-1&&b==1&&c==1&&d==-1) {
			return -1;
		} else
			return 0;
	}
}
int main() {
	int N;
	cin>>N;
	for(int i=1; i<=N; i++) {
		for(int j=1; j<=N; j++) {
			cin>>a[i][j];
		}
	}
	partition(1,1,N);
	int cnt=0;
	for(int i=1; i<=N; i++) {
		for(int j=1; j<=N; j++) {
			if(mark[i][j]==max_size)
				cnt++;
		}
	}
	cout<<max_size<<' '<<cnt<<endl;
	return 0;
}

反思

第十个数据超时了。

原因很简单，有太多重复计算的子问题了，实际上不适合用分治。

这种方法不仅比直接穷举弯弯绕绕，还比穷举效率更低。实际上这道题如果有序地搜索（如DFS），简单明了且效率高，因为可以剪枝很多不必要的搜索。

这道题分治法几乎无法剪枝。在超时之后我思考了一下每个子问题规模减小为二分之一，发现不可行。因为尝试减少子问题重叠的程度，可能会导致有些棋盘无法被覆盖。只能作为判断该二进制矩阵是否为棋盘的方法，但这样还不如直接二重循环判断，于是几乎毫无应用场景。

在这一题想到分治算是一个很大的教训：要在写之前想到更多可能，好好分析效率。

不过，分治法为下面的动态规划做了铺垫，没有子问题的分解思考是很难突然想到动态规划的思路的。

方法二：动态规划

分析与转化

分治法中已经把问题分为四个左上角的子问题。分治法是从顶向下，而动态规划是从底向上。

1.最小的问题显然是在最大的矩阵的最下排和最右列，原本值为1，则为尺寸1的小棋盘；原本值为0，则为尺寸1的取反小棋盘。

2.除去已赋初值的一排一列，从下往上，从右往左遍历填表。

用文字表述或者列出状态转移方程都会比较冗长，因此简述思路，详见代码。

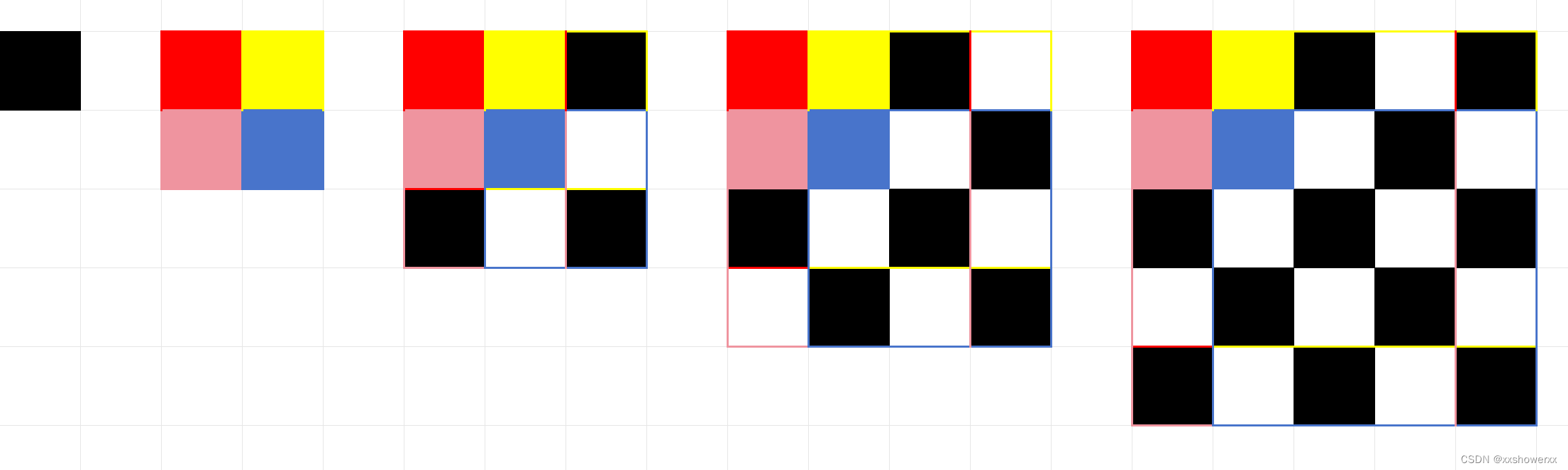
红格是将要填的位置，黄粉蓝是已经填好的四个位置。

只有满足原矩阵中红蓝为1，黄粉为0才至少为一个2x2的棋盘，10取反则为取反棋盘。

dp数组存储的值为以此格为左上角最大尺寸的棋盘/取反棋盘，因此其实符合“木桶原则”，红格满足2x2棋盘或取反棋盘的要求后，红格的dp值是其余三格dp绝对值中的最小值+1。符号表示类型。

不满足这一要求，就以最小规模的问题来解决。

代码

#include<bits/stdc++.h>
using namespace std;
char a[2005][2005];
int mark[2005][2005];
int cnt[2005];
int max_size=1;
int main() {
	int N;
	cin>>N;
	for(int i=1; i<=N; i++) {
		for(int j=1; j<=N; j++) {
			cin>>a[i][j];
		}
	}
	for(int i=1;i<=N;i++){
		if(a[N][i]=='1')
		{
			mark[N][i]=1;
			cnt[1]++;
		}
		else
			mark[N][i]=-1;
		if(a[i][N]=='1')
		{
			mark[i][N]=1;
			cnt[1]++;
		}
		else
			mark[i][N]=-1;
	}
	if(mark[N][N]==1)
		cnt[1]--;
	for(int i=N-1; i>=1; i--) {
		for(int j=N-1; j>=1; j--) {
			if(mark[i+1][j]<0&&mark[i][j+1]<0&&mark[i+1][j+1]>0&&a[i][j]=='1')
			{
				int minMark=min(abs(mark[i+1][j]),abs(mark[i][j+1]));
				minMark=min(minMark,abs(mark[i+1][j+1]));
				mark[i][j]=minMark+1;
				cnt[mark[i][j]]++;
				if(mark[i][j]>max_size){
					max_size=mark[i][j];
				}
			}
			else if(mark[i+1][j]>0&&mark[i][j+1]>0&&mark[i+1][j+1]<0&&a[i][j]=='0')
			{
				int minMark=min(abs(mark[i+1][j]),abs(mark[i][j+1]));
				minMark=min(minMark,abs(mark[i+1][j+1]));
				mark[i][j]=-1*(minMark+1);
			}
			else
			{
				if(a[i][j]=='1')
				{
					mark[i][j]=1;
					cnt[1]++;
				}
				else
					mark[i][j]=-1;
			}
			
		}
	}
	cout<<max_size<<' '<<cnt[max_size]<<endl;
	return 0;
}

反思

做到这里的时候发现我似乎经常用-1处理0，以处理储存问题。如我之前写的CCF-CSP 202012-2期末预测之最佳阈值-CSDN博客

动态规划方法还是不够熟练，总需要有个较差方法的踏板后灵光一现才能想到，实际应试上时间不够我去尝试多次。

时间复杂度三种方法里最小，明显快于分治法，但是和一般的做法相差不大。

方法三：DFS

分析

这一方法相当于题目的直译，采用一种有序的搜索方式即可。应该属于最简单的一种DFS。这题这种方法效率特别高，剪枝的余地很大，源于构成棋盘的要求非常严格。

代码

#include<bits/stdc++.h>
using namespace std;
char a[2005][2005];
int mark[2005];
int max_size=1;
int N;
void expand(int row,int col,int size){
	if(a[row][col]!='1')
		return;
	int flag=0;
	for(int i=row;i<row+size;i++){
		for(int j=col;j<col+size;j++){
			if((i-row+j-col)%2==0&&a[i][j]=='0')
			{
				flag=1;
				break;
			}
			else if((i-row+j-col)%2==1&&a[i][j]=='1')
			{
				flag=1;
				break;
			}
		}
		if(flag==1)
			break;
	}
	if(!flag){
		if(size>=max_size)
		{
			max_size=size;
			mark[max_size]++;
		}
		if(row+size<=N&&col+size<=N)
			expand(row,col,size+1);
	}
}
int main() {
	cin>>N;
	for(int i=1; i<=N; i++) {
		for(int j=1; j<=N; j++) {
			cin>>a[i][j];
		}
	}
	for(int i=1; i<=N; i++) {
		for(int j=1; j<=N; j++) {
			expand(i,j,1);
		}
	}
	cout<<max_size<<' '<<mark[max_size]<<endl;
	return 0;
}

反思

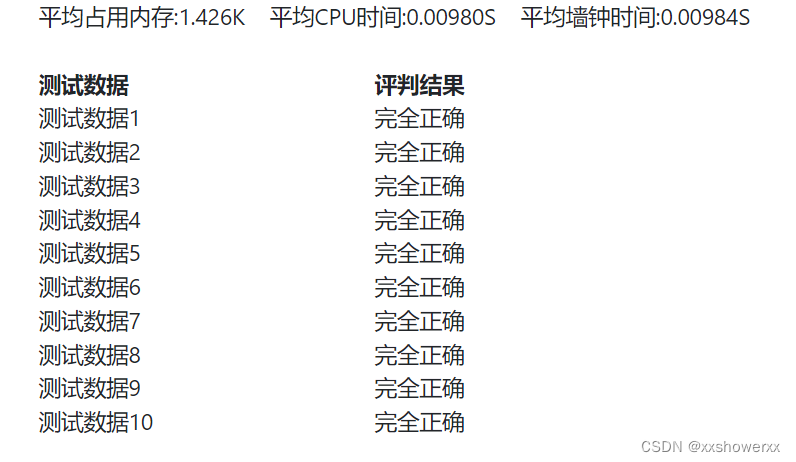对比下来分治法太惨烈了，动态规划的效率优化也几乎毫无意义。

下次再也不随便下手了（显然还会犯）