基于 Erlang 分布的 SEIR 模型：用离散事件模拟传染病动态传播

于 2025-05-28 01:15:00 发布
阅读量1k 收藏 17
点赞数 19
分类专栏： 传染病模型，看这一个就够了！ 文章标签： 数学建模 matlab 传染病 微分方程
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/xyhxx99499/article/details/148166000
版权

在传染病建模领域，SEIR 模型（易感 - 暴露 - 感染 - 康复）因其能够刻画潜伏期和感染期的动态过程，成为比 SIR 模型更贴近现实的选择。而通过引入 Erlang 分布描述暴露和感染阶段的持续时间，我们可以更灵活地模拟真实世界中潜伏期和传染期的变异性。今天，我们结合 MATLAB 代码，深入解析如何用离散事件模拟构建高保真的 SEIR 模型。

一、SEIR 模型升级：从指数分布到 Erlang 分布 📈

1. 传统 SEIR 模型的局限

传统模型假设潜伏期和感染期服从指数分布（无记忆性），但现实中：

  • 新冠病毒潜伏期多为 3-7 天（非指数分布）
  • 流感传染期通常集中在发病后 2-4 天（存在峰值）

2. Erlang 分布的优势

Erlang 分布通过形状参数k和速率参数\(\gamma\)，能够：

  • 拟合非指数分布的持续时间（如正态分布、伽马分布）
  • 当\(k=1\)时退化为指数分布
  • 当k增大时，分布趋近于正态分布（方差减小）

二、核心函数解析：计算 Erlang 离散概率 🧮

1. compute_erlang_discrete_prob函数逻辑

function density_prob = compute_erlang_discrete_prob(k, gamma)
    n_bin = 0;
    factorials = 1;  % 预计算阶乘（0! = 1）
    for i = 1:k
        factorials(i+1) = factorials(i) * i;  % i! = (i-1)! * i
    end

    one_sub_cummulative_probs = [];
    cummulative_prob = 0;
    while cummulative_prob <= 0.99  % 累积概率达99%时停止分箱
        n_bin = n_bin + 1;
        prob = 0;
        for j = 0:(k-1)
            % Erlang分布的概率质量函数（离散近似）
            prob = prob + (exp(-n_bin * gamma) * (n_bin * gamma)^j) / factorials(j+1);
        end
        one_sub_cummulative_probs(end+1) = prob;
        cummulative_prob = 1 - prob;  % 1 - P(N <= n_bin)
    end
    one_sub_cummulative_probs = [1, one_sub_cummulative_probs];  % 补全初始概率
    
    % 计算密度概率（相邻累积概率之差）
    density_prob = diff(one_sub_cummulative_probs) / cummulative_prob;
end

2. 关键步骤解读

  • 阶乘预计算：通过循环预存\(0!\)到\(k!\)，避免重复计算
  • 分箱策略：通过循环增加分箱数\(n\_bin\)，直到尾部概率\(\leq 1\%\)
  • 离散近似：将连续 Erlang 分布转换为离散概率向量，用于多项分布抽样
  • 归一化：用总有效概率（\(\leq 99\%\)部分）归一化密度概率

三、SEIR 模拟引擎：基于离散事件的仓室动态 🕒

1. 参数与状态初始化

function sim_data = seir_simulation(initial_state, parameters, max_time)
    % 状态容器（键值对存储，便于扩展）
    initial_state = containers.Map({'S', 'E', 'I', 'R'}, initial_state);
    params = containers.Map(...
        {'erlang_shape_for_E', 'erlang_rate_for_E',  % 暴露期参数
         'erlang_shape_for_I', 'erlang_rate_for_I',  % 感染期参数
         'base_transmission_rate'}, parameters);
    
    % 初始化模拟数据结构
    sim_data = struct('time', 1:max_time, 'S', [], 'E', [], 'I', [], 'R', []);
    [sim_data.S(1), sim_data.E(1), sim_data.I(1), sim_data.R(1)] = ...
        deal(initial_state('S'), initial_state('E'), initial_state('I'), initial_state('R'));

2. 暴露期与感染期的区块建模 

% 暴露期区块（每个区块对应Erlang分布的一个阶段）
exposed_block_adm_rates = compute_erlang_discrete_prob(...
    params('erlang_shape_for_E'), params('erlang_rate_for_E'));
exposed_blocks = zeros(max_time, length(exposed_block_adm_rates));
exposed_blocks(1, end) = sim_data.E(1);  % 初始暴露者位于最后一个区块

% 感染期区块（逻辑同上）
infectious_block_adm_rates = compute_erlang_discrete_prob(...
    params('erlang_shape_for_I'), params('erlang_rate_for_I'));
infectious_blocks = zeros(max_time, length(infectious_block_adm_rates));
infectious_blocks(1, end) = sim_data.I(1);

3. 动态转移逻辑 

for time = 2:max_time
    % 计算感染压力
    transmission_rate = params('base_transmission_rate') * sim_data.I(time-1);
    exposure_prob = 1 - exp(-transmission_rate / population_size);
    
    % 新暴露者（二项分布抽样）
    new_exposed = binornd(sim_data.S(time-1), exposure_prob);
    
    % 暴露期转移（区块左移，新暴露者进入最后一个区块）
    exposed_blocks(time, :) = [exposed_blocks(time-1, 2:end), 0] + ...
        (new_exposed > 0 ? mnrnd(new_exposed, exposed_block_adm_rates) : 0);
    
    % 感染期与康复期转移（逻辑类似）
    new_infectious = exposed_blocks(time-1, 1);  % 第一区块为成熟暴露者
    infectious_blocks(time, :) = [infectious_blocks(time-1, 2:end), 0] + ...
        (new_infectious > 0 ? mnrnd(new_infectious, infectious_block_adm_rates) : 0);
    
    % 更新仓室数量
    sim_data.S(time) = sim_data.S(time-1) - new_exposed;
    sim_data.E(time) = sum(exposed_blocks(time, :));
    sim_data.I(time) = sum(infectious_blocks(time, :));
    sim_data.R(time) = sim_data.R(time-1) + infectious_blocks(time-1, 1);
end

四、模拟实战：参数设置与结果分析 📊

1. 运行示例

initial_state = [9999, 1, 0, 0];  % S=9999, E=1, I=0, R=0
parameters = [5, 1, 10, 1, 0.25];  % E期(k=5, γ=1), I期(k=10, γ=1), β=0.25
max_time = 300;
sim = seir_simulation(initial_state, parameters, max_time);

2. 结果可视化 

figure;
hold on;
plot(sim.time, sim.S, 'b-', 'LineWidth', 2);  % 易感者
plot(sim.time, sim.E, 'g--', 'LineWidth', 2);  % 暴露者
plot(sim.time, sim.I, 'r-.', 'LineWidth', 2);  % 感染者
plot(sim.time, sim.R, 'm:', 'LineWidth', 2);  % 康复者
xlabel('Time'); ylabel('Population');
legend('Susceptible', 'Exposed', 'Infectious', 'Recovered');

3. 趋势解读

 

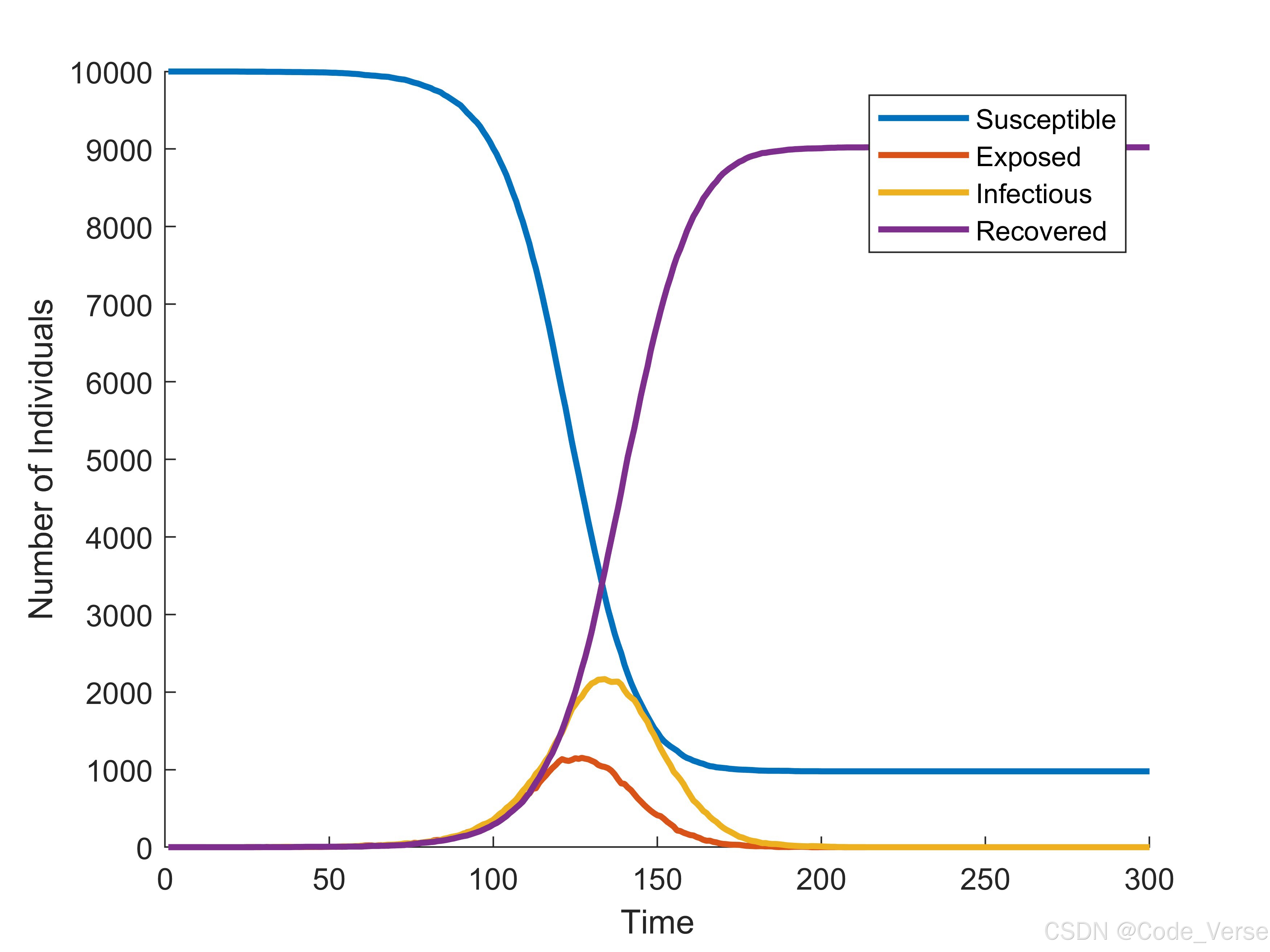
  • 易感者（S）：随感染压力持续下降，最终趋于稳定
  • 暴露者（E）：初期快速增长，受潜伏期 Erlang 分布影响，峰值略滞后于感染期
  • 感染者（I）：呈现典型单峰曲线，峰值由感染率和康复率共同决定
  • 康复者（R）：随感染人数增加而单调上升，反映累计康复量

五、模型扩展与应用场景 💡

1. 参数敏感性分析

  • 形状参数k：增大k会使潜伏期 / 感染期分布更集中（如 k=10 时接近正态分布）
  • 速率参数\(\gamma\)：决定平均持续时间（如\(\gamma=1\)时，E 期平均 5 天，I 期平均 10 天）
  • 基础传播率\(\beta\)：直接影响疫情峰值高度和到达时间

2. 现实场景适配

  • COVID-19 建模：设置 E 期 k=3（近似 3 天潜伏期），I 期 k=5（传染期集中在 5 天内）
  • 流感模拟：使用指数分布（k=1）模拟较短且随机的传染期
  • 疫苗效果评估：通过降低\(\beta\)或增加康复率，对比不同防控措施效果

3. 局限性与改进方向

  • 当前局限：假设均匀混合群体，未考虑空间异质性
  • 升级方向：
    • 引入年龄分层（如分儿童 / 成人 / 老人仓室）
    • 结合地理信息，模拟区域间传播
    • 添加随机扰动项，模拟政策干预的突发影响

结语：用数学模型照亮传染病防控之路 🌟

通过 Erlang 分布与离散事件模拟的结合，我们构建了一个既保持数学严谨性，又能灵活适配现实数据的 SEIR 模型。这种方法不仅适用于传染病研究，还可扩展到供应链库存管理、排队系统优化等领域。正如代码中通过分箱和抽样实现的动态转移，现实中的疫情防控也需要在 “精准建模” 与 “灵活应对” 之间找到平衡。希望这段代码能为你的研究或应用提供启发，让数据驱动的决策更具科学性～🚀

互动思考：如果要模拟 Delta 和 Omicron 变种的传播差异，你会如何调整 Erlang 分布参数？欢迎在评论区分享你的思路！

 完整代码（省流版）

function density_prob = compute_erlang_discrete_prob(k, gamma)
    n_bin = 0;
    factorials = 1;  % 0! = 1
    for i = 1:k
        factorials(i+1) = factorials(i) * i;  % factorials(i+1) = i!
    end

    one_sub_cummulative_probs = [];
    cummulative_prob = 0;
    while cummulative_prob <= 0.99
        n_bin = n_bin + 1;
        one_sub_cummulative_probs(n_bin) = 0;
        for j = 0:(k-1)
            one_sub_cummulative_probs(n_bin) = ...
                one_sub_cummulative_probs(n_bin) + ...
                (exp(-n_bin * gamma) * (n_bin * gamma)^j) / factorials(j+1);
        end
        cummulative_prob = 1 - one_sub_cummulative_probs(n_bin);
    end
    one_sub_cummulative_probs = [1, one_sub_cummulative_probs];

    density_prob = one_sub_cummulative_probs(1:end-1) - one_sub_cummulative_probs(2:end);
    density_prob = density_prob / cummulative_prob;
end

function sim_data = seir_simulation(initial_state, parameters, max_time)
    initial_state = containers.Map({'S', 'E', 'I', 'R'}, initial_state);
    params = containers.Map(...
        {'erlang_shape_for_E', 'erlang_rate_for_E', ...
         'erlang_shape_for_I', 'erlang_rate_for_I', ...
         'base_transmission_rate'}, ...
         parameters);
    
    population_size = sum(cell2mat(values(initial_state)));
    sim_data = struct(...
        'time', 1:max_time, ...
        'S', zeros(max_time, 1), ...
        'E', zeros(max_time, 1), ...
        'I', zeros(max_time, 1), ...
        'R', zeros(max_time, 1));
    sim_data.S(1) = initial_state('S');
    sim_data.E(1) = initial_state('E');
    sim_data.I(1) = initial_state('I');
    sim_data.R(1) = initial_state('R');

    % 初始化暴露区块
    exposed_block_adm_rates = compute_erlang_discrete_prob(...
        params('erlang_shape_for_E'), params('erlang_rate_for_E'));
    n_exposed_blocks = length(exposed_block_adm_rates);
    exposed_blocks = zeros(max_time, n_exposed_blocks);
    exposed_blocks(1, end) = sim_data.E(1);

    % 初始化感染区块
    infectious_block_adm_rates = compute_erlang_discrete_prob(...
        params('erlang_shape_for_I'), params('erlang_rate_for_I'));
    n_infectious_blocks = length(infectious_block_adm_rates);
    infectious_blocks = zeros(max_time, n_infectious_blocks);
    infectious_blocks(1, end) = sim_data.I(1);

    for time = 2:max_time
        transmission_rate = params('base_transmission_rate') * sim_data.I(time-1) / population_size;
        exposure_prob = 1 - exp(-transmission_rate);

        new_exposed = binornd(sim_data.S(time-1), exposure_prob);
        new_infectious = exposed_blocks(time-1, 1);
        new_recovered = infectious_blocks(time-1, 1);

        if new_exposed > 0
            exposed_blocks(time, :) = mnrnd(new_exposed, exposed_block_adm_rates(:)');
        end
        exposed_blocks(time, :) = exposed_blocks(time, :) + ...
            [exposed_blocks(time-1, 2:end), 0];

        if new_infectious > 0
            infectious_blocks(time, :) = mnrnd(new_infectious, infectious_block_adm_rates(:)');
        end
        infectious_blocks(time, :) = infectious_blocks(time, :) + ...
            [infectious_blocks(time-1, 2:end), 0];

        sim_data.S(time) = sim_data.S(time-1) - new_exposed;
        sim_data.E(time) = sum(exposed_blocks(time, :));
        sim_data.I(time) = sum(infectious_blocks(time, :));
        sim_data.R(time) = sim_data.R(time-1) + new_recovered;
    end
end

% 运行模拟
initial_state = [9999, 1, 0, 0];
parameters = [5, 1, 10, 1, 0.25];
max_time = 300;
sim = seir_simulation(initial_state, parameters, max_time);

% 绘图
figure;
hold on;
plot(sim.time, sim.S, 'LineWidth', 2, 'DisplayName', 'Susceptible');
plot(sim.time, sim.E, 'LineWidth', 2, 'DisplayName', 'Exposed');
plot(sim.time, sim.I, 'LineWidth', 2, 'DisplayName', 'Infectious');
plot(sim.time, sim.R, 'LineWidth', 2, 'DisplayName', 'Recovered');
xlabel('Time');
ylabel('Number of Individuals');
legend('show');
hold off;
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值