经典地理建模分析方法

线性代数知识

1，特征值、特征向量计算

相关分析

单相关系数

实例：分析气温与降雨量的相关关系。

根据列表，带入数据计算即可。结果表明呈负相关关系，异向相关。

检验：

本例中f=12-2=10；再查表可知相关关系不显著。

秩相关系数

又称等级相关系数，或顺序相关系数,是将两要素的样本值按数据的大小顺序排列位次，以各要素样本值的位次代替实际数据而求得的一种统计量。


即：GDP（x）与总人口（ y ）之间的等级相关系数为0.7847。
检验，看n的大小，查表比较相关系数与表中值的大小得出结论。

偏相关系数

只研究两个要素之间的相关关系，其他要素暂时不考虑。
一级偏相关系数

二级偏相关系数

例如：对于某4个地理要素x1，x2，x3，x4的23个样本数据，经过计算得到了如下的单相关系数矩阵：

检验

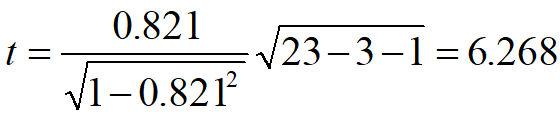
复相关系数

例题：在上例中，若以x4为因变量，x1，x2，x3为自变量，试计算x4与x1，x2，x3之间的复相关系数。

回归分析

线性回归

定义：假设有两个地理要素（变量）x 和y，x为自变量，y为因变量。则一元线性回归模型的基本结构形式为

总的离差平方和：在回归分析中，表示y的n次观测值之间的差异，记为

例题：把表格中降水P看做因变量，维度y和海拔a看做自变量，建立p与y、a的线性回归模型。
1，对着表格，列出自变量X矩阵和因变量Y矩阵。

$X=\left(\begin{array}{ccc}1& 40.5& 1170.80\\ 1& 36.60& 1707.20\\ ...& ...& ...\\ 1& 36.14& 1111.70\end{array}\right)$

其中X矩阵，第一列为常数、第二、三列对应着自变量y和a。

$Y=\left(\begin{array}{c}48.25\\ 193.72\\ ...\\ 574.00\end{array}\right)$

其中Y矩阵为因变量p

2，求矩阵b

$b=\left(\begin{array}{c}{b}_1\\ b_2\\ b_3\end{array}\right)=(X^{T}Y{)}^{-1}\ast (X^{T}Y)$

3,把b的值带入方程

y=$b_0+b_1\ast x_1+b_2\ast x_2$

4,检验

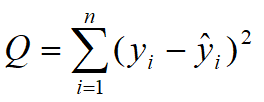
F越大，模型的效果越佳。

非线性回归模型

步骤：
1，非线性线性化
2，做散点图看看是不是线性关系
3，建立线性回归方程，计算相关系数
4，还原为非线性方程

主成分分析

1.计算相关系数矩阵
2.计算特征值与特征向量
3.计算主成分贡献率及累计贡献率


一般取累计贡献率达85%~95%的特征值
4.计算主成分载荷

5.各主成分的得分

趋势面分析

趋势面分析，是利用数学曲面模拟地理系统要素在空间上的分布及变化趋势的一种数学方法。它实质上是通过回归分析原理，运用最小二乘法拟合一个二维非线性函数，模拟地理要素在空间上的分布规律，展示地理要素在地域空间上的变化趋势。
通常把实际的地理曲面分解为趋势面和剩余面两部分，前者反映地理要素的宏观分布规律，属于确定性因素作用的结果；而后者则对应于微观局域，是随机因素影响的结果。
趋势面分析的一个基本要求，就是所选择的趋势面模型应该是剩余值最小，而趋势值最大，这样拟合度精度才能达到足够的准确性。空间趋势面分析，正是从地理要素分布的实际数据中分解出趋势值和剩余值，从而揭示地理要素空间分布的趋势与规律。
从实际观测值出发推算趋势面，一般采用回归分析方法，使得残差平方和趋于最小

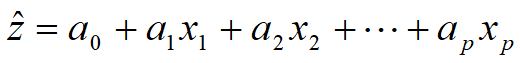
在实际应用中，往往用次数低的趋势面逼近变化比较小的地理要素数据，用次数高的趋势面逼近起伏变化比较复杂的地理要素数据。次数低的趋势面使用起来比较方便，但具体到某点拟合较差；次数较高的趋势面只在观测点附近效果较好，而在外推和内插时则效果较差。

聚类分析

也称为群分析、点群分析。按照样本自身数学，用数学方法按相似性或差异性指标确定样本之间的亲疏关系。并按照亲疏关系对样本进行聚类。
主要有系统聚类、模糊聚类和动态聚类。
1，系统聚类
使用聚类衡量样本之间的差异；计算样本之间的距离，首先将各个样本视为单独的类别。根据距离最小原则，依次选出一对样本，归并为新类。如果样本之前已经属于一个类别，则把之前类别归并为新类。
每次归并的新类，采取距离计算方法归并（最短、最远、中线、重心、组平均、距离平方、可变数、可变法）