原文:http://www.cnblogs.com/Booble/archive/2011/03/04/1970453.html
参考:http://community.topcoder.com/tc?module=Static&d1=tutorials&d2=maxFlow
对原文作了细微的修改。
一.网络流:流&网络&割
1.网络流问题(NetWork Flow Problem):
给定指定的一个有向图,其中有两个特殊的点源S(Sources)和汇T(Sinks),每条边有指定的容量(Capacity),求满足条件的从S到T的最大流(MaxFlow).
The network flow problem considers a graph G with a set of sources S and sinks T and for which each edge has an assigned capacity (weight), and then asks to find the maximum flow that can be routed from S to T while respecting the given edge capacities.
http://mathworld.wolfram.com/NetworkFlow.html

下面给出一个通俗点的解释
(下文基本避开形式化的证明 基本都用此类描述叙述)
好比你家是汇 自来水厂(有需要的同学可以把自来水厂当成银行之类 以下类似)是源
然后自来水厂和你家之间修了很多条水管子接在一起 水管子规格不一 有的容量大 有的容量小
然后问自来水厂开闸放水 你家收到水的最大流量是多少
如果自来水厂停水了 你家那的流量就是0 当然不是最大的流量
但是你给自来水厂交了100w美金 自来水厂拼命水管里通水 但是你家的流量也就那么多不变了 这时就达到了最大流
-------------------------------------------------------------------------------------------------------------
2.三个基本的性质:
如果 C代表每条边的容量 F代表每条边的流量
一个显然的实事是F小于等于C 不然水管子就爆了
这就是网络流的第一条性质 容量限制(Capacity Constraints):F<x,y> ≤ C<x,y>
再考虑节点任意一个节点 流入量总是等于流出的量 否则就会蓄水(爆炸危险...)或者平白无故多出水(有地下水涌出?)
这是第二条性质 流量守恒(Flow Conservation):Σ F<v,x> = Σ F<x,u>
当然源和汇不用满足流量守恒 我们不用去关心自来水厂的水是河里的 还是江里的
最后一个不是很显然的性质 是斜对称性(Skew Symmetry): F<x,y> = - F<y,x>
这其实是完善的网络流理论不可缺少的 就好比中学物理里用正负数来定义一维的位移一样
百米起点到百米终点的位移是100m的话 那么终点到起点的位移就是-100m
同样的 x向y流了F的流 y就向x流了-F的流
-------------------------------------------------------------------------------------------------------------
3.容量网络&流量网络&残留网络:
网络就是有源汇的有向图 关于什么就是指边权的含义是什么
容量网络就是关于容量的网络 基本是不改变的(极少数问题需要变动)

流量网络就是关于流量的网络 在求解问题的过程中
通常在不断的改变 但是总是满足上述三个性质
调整到最后就是最大流网络 同时也可以得到最大流值

残留网络往往概括了容量网络和流量网络 是最为常用的
残留网络=容量网络-流量网络
这个等式是始终成立的 残留值当流量值为负时甚至会大于容量值
流量值为什么会为负?有正必有负,记住斜对称性!

-------------------------------------------------------------------------------------------------------------
4.割&割集:
无向图的割集(Cut Set):C[A,B]是将图G分为A和B两个点集 A和B之间的边的全集
A set of edges of a graph which, if removed (or "cut"), disconnects the graph (i.e., forms a disconnected graph).
http://mathworld.wolfram.com/CutSet.html
网络的割集:C[S,T]是将网络G分为s和t两部分点集 S属于s且T属于t 从S到T的边的全集
带权图的割(Cut)就是割集中边或者有向边的权和
Given a weighted, undirected graph G=(V,E) and a graphical partition of V into two sets A and B, the cut of G with respect to A and B is defined as cut(A,B)=sum_(i in A,j in B)W(i,j),where W(i,j) denotes the weight for the edge connecting vertices i and j. The weight of the cut is the sum of weights of edges crossing the cut.
http://mathworld.wolfram.com/Cut.html

通俗的理解一下:
割集好比是一个恐怖分子 把你家和自来水厂之间的水管网络砍断了一些
然后自来水厂无论怎么放水 水都只能从水管断口哗哗流走了 你家就停水了
割的大小应该是恐怖分子应该关心的事 毕竟细管子好割一些
而最小割花的力气最小
==================================================================================
二.计算最大流的基本算法
那么怎么求出一个网络的最大流呢?
这里介绍一个最简单的算法:Edmonds-Karp算法 即最短路径增广算法 简称EK算法
EK算法基于一个基本的方法:Ford-Fulkerson方法 即增广路方法 简称FF方法
增广路方法是很多网络流算法的基础 一般都在残留网络中实现
其思路是:每次找出一条从源到汇的能够增加流的路径 调整流值和残留网络 不断调整直到没有增广路为止
FF方法的基础是增广路定理(Augmenting Path Theorem):网络达到最大流当且仅当残留网络中没有增广路
证明略 这个定理应该能够接受的吧
EK算法就是不断的找最短路 找的方法就是每次找一条边数最少的增广 也就是最短路径增广
这样就产生了三个问题:
-------------------------------------------------------------------------------------------------------------
1.最多要增广多少次?
可以证明 最多O(VE)次增广 可以达到最大流 证明略
2.如何找到一条增广路?
先明确什么是增广路 增广路是这样一条从s到t的路径 路径上每条边残留容量都为正
把残留容量为正的边设为可行的边 那么我们就可以用简单的BFS得到边数最少的增广路
3.如何增广?
BFS得到增广路之后 这条增广路能够增广的流值 是路径上最小残留容量边决定的
把这个最小残留容量MinCap值加到最大流值Flow上 同时路径上每条边的残留容量值减去MinCap
最后 路径上每条边的反向边残留容量值要加上MinCap 为什么? 下面会具体解释
-------------------------------------------------------------------------------------------------------------
这样每次增广的复杂度为O(E) EK算法的总复杂度就是O(VE^2)
事实上 大多数网络的增广次数很少 EK算法能处理绝大多数问题
平均意义下增广路算法都是很快的
增广路算法好比是自来水公司不断的往水管网里一条一条的通水
上面还遗留了一个反向边的问题: 为什么增广路径上每条边的反向边残留容量值要加上MinCap?
因为斜对称性! 由于残留网络=容量网络-流量网络
容量网络不改变的情况下
由于增广好比给增广路上通了一条流 路径说所有边流量加MinCap
流量网络中路径上边的流量加MinCap 反向边流量减去MinCap
相对应的残留网络就发生相反的改变
这样我们就完成了EK算法 具体实现可以用邻接表存图 也可以用邻接矩阵存图
邻接表存图 由于流量同时存在于边与反向边 为了方便求取反向边 建图把一对互为反向边的边建在一起
(补充)下面是使用BFS找最短路径实现的最大流算法,不断调用该函数,直到没有最短路径为止。
int bfs()
queue Q
push source to Q
mark source as visited
keep an array from with the semnification: from[x] is the
previous vertex visited in the shortest path from the source to x;
initialize from with -1 (or any other sentinel value)
while Q is not empty
where = pop from Q
for each vertex next adjacent to where
if next is not visited and capacity[where][next] > 0
push next to Q
mark next as visited
from[next] = where
if next = sink
exit while loop
end for
end while
// we compute the path capacity
where = sink, path_cap = infinity
while from[where] > -1
prev = from[where] // the previous vertex
path_cap = min(path_cap, capacity[prev][where])
where = prev
end while
// we update the residual network; if no path is found the while
loop will not be entered
where = sink
while from[where] > -1
prev = from[where]
capacity[prev][where] -= path_capacity
capacity[where][prev] += path_capacity
where = prev
end while
// if no path is found, path_cap is infinity
if path_cap = infinity
return 0
else return path_cap
==================================================================================
三.最大流最小割定理
下面介绍网络流理论中一个最为重要的定理
最大流最小割定理(Maximum Flow, Minimum Cut Theorem):网络的最大流等于最小割
The maximum flow between vertices v_i and v_j in a graph G is exactly the weight of the smallest set of edges to disconnect G with v_i and v_j in different components.
http://mathworld.wolfram.com/MaximumFlowMinimumCutTheorem.html
具体的证明分三部分
1.任意一个流都小于等于任意一个割
这个很好理解 自来水公司随便给你家通点水 构成一个流
恐怖分子随便砍几刀 砍出一个割
由于容量限制 每一根的被砍的水管子流出的水流量都小于管子的容量
每一根被砍的水管的水本来都要到你家的 现在流到外面 加起来得到的流量还是等于原来的流
管子的容量加起来就是割 所以流小于等于割
由于上面的流和割都是任意构造的 所以任意一个流小于任意一个割
2.构造出一个流等于一个割
当达到最大流时 根据增广路定理
残留网络中s到t已经没有通路了 否则还能继续增广
我们把s能到的的点集设为S 不能到的点集为T
构造出一个割集C[S,T] S到T的边必然满流 否则就能继续增广
这些满流边的流量和就是当前的流即最大流
把这些满流边作为割 就构造出了一个和最大流相等的割
3.最大流等于最小割
设相等的流和割分别为Fm和Cm
则因为任意一个流小于等于任意一个割
任意F≤Fm=Cm≤任意C
定理说明完成
(补充)关于这个证明我感觉下面解释的比较好。
原文:http://community.topcoder.com/tc?module=Static&d1=tutorials&d2=maxFlow
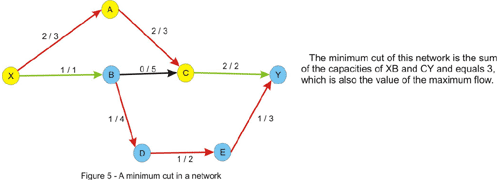
最大流、最小割定理(Maximum Flow, Minimum Cut Theorem):网络的最大流等于最小割。
We will assume that we are in the situation in which no augmenting path in the network has been found. Let's color in yellow, like in the figure above, every vertex that is reachable by a path that starts from the source and consists of non-full forward edges and of non-empty backward edges. Clearly the sink will be colored in blue, since there is no augmenting path from the source to the sink. Now take every edge that has a yellow starting point and a blue ending point. This edge will have the flow equal to the capacity, otherwise we could have added this edge to the path we had at that point and color the ending point in yellow. Note that if we remove these edges there will be no directed path from the source to the sink in the graph. Now consider every edge that has a blue starting point and a yellow ending point. The flow on this edge must be 0 since otherwise we could have added this edge as a backward edge on the current path and color the starting point in yellow. Thus, the value of the flow must equal the value of the cut, and since every flow is less or equal to every cut, this must be a maximum flow, and the cut is a minimum cut as well.
==================================================================================
四.简单的应用
http://community.topcoder.com/stat?c=problem_statement&pm=1931&rd=4709
(补充)Tricks
1. 对于多源多汇问题,只需要添加一个超源点和一个超汇点,将其转化为单源单汇问题即可,如下图。
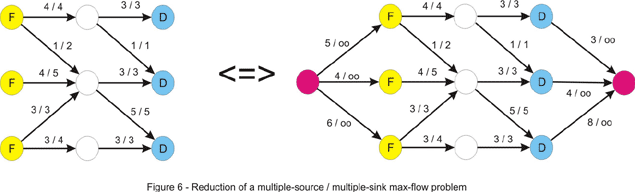
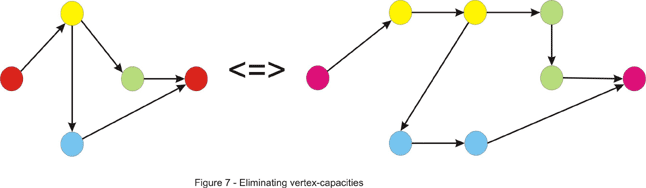
2. 对于在顶点处有流量限制的问题,可以对源图进行扩展,既构建一个新的图,新的图的顶点数是源图的两倍,
源图中每个顶点对应新图中的两个顶点,新的顶点之间有一条边相连,边的权值就是源图顶点的权值,如下图。





















 2万+
2万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








