群论。。。

群论

群论，是数学概念。在数学和抽象代数中，群论研究名为群的代数结构。群在抽象代数中具有基本的重要地位：许多代数结构，包括环、域和模等可以看作是在群的基础上添加新的运算和公理而形成的。群的概念在数学的许多分支都有出现，而且群论的研究方法也对抽象代数的其它分支有重要影响。群论的重要性还体现在物理学和化学的研究中，因为许多不同的物理结构，如晶体结构和氢原子结构可以用群论方法来进行建模。于是群论和相关的群表示论在物理学和化学中有大量的应用。

群

基本概念

子群

注： 若干个 子群的交仍为子群，但一般来说，若干个子群的并却不一定为子群.

陪集

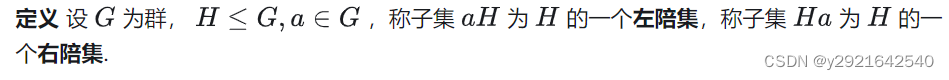
环

定义

注：如果环的乘法满足交换律，则称环为交换环。

环的单位群

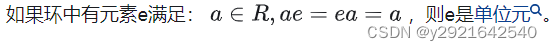
注： 如果存在单位元，则单位元是唯一的。

域

域(Field)在交换环的基础上，还增加了二元运算除法，要求元素(除零以外)可以作除法运算，即每个非零的元素都要有乘法逆元。由此可见，域是一种可以进行加减乘除(除0以外)的代数结构，是数域与四则运算的推广。

伽罗华域（GF）

伽罗华域也称为有限域，域( R , + , − , ⋅ , ÷ ) (R,+,-,\cdot,\div)(R,+,−,⋅,÷)由运算元素集合和四则运算组成，由于减法、除法分别和加法、乘法是逆运算关系，只需要关注加法和乘法即可。对于加法来说，每个元素要求有对应的加法逆元；对于乘法来说，除0以外的每个元素要求要有对应的乘法逆元。

伽罗华域G F ( q )表示

q指有限域的阶，在有限域中阶等于元素个数，有限域的阶通常是素数P或是素数幂P^W ，即q = P 或 q =P^W.

有限域GF（P）

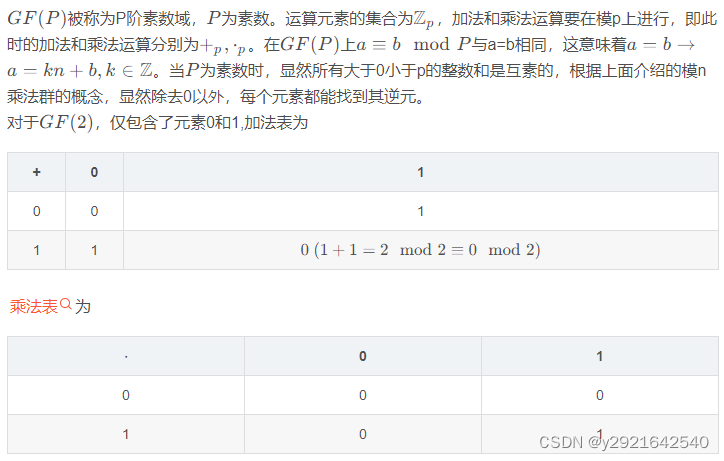
有限域GF（P^ω）

群论 线代

线性代数是研究向量空间、线性映射以及这两个概念的基础理论。从群论的角度看，线性代数可以被视为一种特殊的群论，其中研究的对象是向量空间上的特定群。
在线性代数中，向量空间是一个带有加法和标量乘法运算的代数结构，其加法运算构成一个阿贝尔群。这意味着向量空间中的加法满足封闭性、结合律、单位元（零向量）和逆元。标量乘法则满足分配律和结合律。因此，线性代数中的基本操作都是在群和环（向量空间加上标量乘法）的范畴内进行的。
从群论的角度理解线性代数，可以将线性变换视为群同态。群同态是一种保持群结构的映射，即它将一个群中的元素映射到另一个群中的元素，并保持群的运算。在线性代数中，线性变换将一个向量空间映射到另一个向量空间，并保持向量加法和标量乘法的运算。例如，矩阵乘法可以看作是一种线性变换，它将一个向量空间中的向量映射到另一个向量空间中的向量。
此外，群论中的群表示论为线性代数提供了另一种视角。群表示论研究群的线性表示，即群的元素如何通过线性变换来表示。这种表示通常通过矩阵来实现，因此，群表示论与线性代数紧密相关。通过群表示论，可以将群论中的概念和结果应用于线性代数问题，从而深化对线性代数的理解。

抽象代数总结

抽象代数是研究各种代数结构的一般理论，包括群、环、域、向量空间等。学习抽象代数系统是为了更好地理解和掌握这些代数结构的基本性质和运算规律，从而为其他数学分支和实际应用提供基础。

1. 代数结构的概念：代数结构是由一组元素和一组运算组成的系统。这些运算在元素上满足一定的公理，如结合律、交换律、单位元和逆元等。了解不同代数结构的概念和性质是学习抽象代数的基础。
2. 群论：群是一种基本的代数结构，由一组元素和一种运算组成。群论研究群的基本性质、分类和结构。学习群论可以帮助我们更好地理解对称性和变换规律。
3. 环和域：环和域是比群更复杂的代数结构，它们包含两种运算：加法和乘法。环和域的研究有助于我们理解代数方程和多项式理论，并在密码学、编码理论应用。
4. 向量空间：向量空间是一种具有线性结构的代数系统，包括向量、标量和线性映射等概念。学习向量空间有助于我们理解线性方程组、线性变换和矩阵理论。
5. 同态和同构：同态和同构是研究代数结构之间关系的重要概念。它们可以帮助我们理解不同代数结构之间的相似性和差异性。
6. 代数表示论：代数表示论研究代数结构的线性表示，即群的元素如何通过线性变换来表示。学习代数表示论有助于我们理解群、环和域的更深层次性质。
7. 数论和代数几何：数论和代数几何是抽象代数的重要应用领域。它们研究整数、多项式和方程的性质，并在密码学、编码理论和计算机科学等领域得到应用。

学习抽象代数系统是为了掌握各种代数结构的基本性质和运算规律，从而为其他数学分支和实际应用提供基础。通过学习抽象代数，我们可以培养严密的逻辑思维能力、抽象概括能力和解决问题的能力。