Query
Time Limit: 20000/10000 MS (Java/Others) Memory Limit: 65536/65536 K (Java/Others)Total Submission(s): 2114 Accepted Submission(s): 735
Your task is to answer next queries:
1) 1 a i c - you should set i-th character in a-th string to c;
2) 2 i - you should output the greatest j such that for all k (i<=k and k<i+j) s1[k] equals s2[k].
Next T blocks contain each test.
The first line of test contains s1.
The second line of test contains s2.
The third line of test contains Q.
Next Q lines of test contain each query:
1) 1 a i c (a is 1 or 2, 0<=i, i<length of a-th string, 'a'<=c, c<='z')
2) 2 i (0<=i, i<l1, i<l2)
All characters in strings are from 'a'..'z' (lowercase latin letters).
Q <= 100000.
l1, l2 <= 1000000.
Then for each query "2 i" output in single line one integer j.
1 aaabba aabbaa 7 2 0 2 1 2 2 2 3 1 1 2 b 2 0 2 3
Case 1: 2 1 0 1 4 1
题意:
给两个字符串,有两种操作。
1、改变一字符串的某个位置的一个字符。
2、询问某一位置开始的最大的连续的两串相同的字符的个数。
解题思路:
首先是简单容易理解得解法。对于题目的询问操作。如果询问的是第p位置。如果我们知道角标大于等于p位置且字符不匹配的第一个位置q。那么答案就是q-p。比如:
012345
aabbccd
aabeccd
对于p=0时。角标大于等于p且字符不匹配的第一个位置q=3。那么ans=3-0=3。
现在的问题时怎样快速维护这一信息。学习过set后知道set有一个强大的功能。
lower_bound(p)函数可以返回键值比p大的第一个值。所以这下就好办了。
开始预处理。扫描一下两个字符串。把字符不相同的位置加到set中。
对于每一个询问。只需返回lower_bound(p)-p就行了。
对于每一个修改。如果修改后的状态和原状态不同。如果原来匹配现在不匹配了。就把角标加入set。
如果原来不匹配而现在匹配了就将这个角标从set中删除。
要注意的是预处理是要将最大字符串长度+1的位置加入到set中。因为如果两个字符完全一样就悲剧了。
因为set中没有值,如果询问的话返回值就是0。于是我就这么奉献了一wa。。TT。
详细见代码:
#include <iostream>
#include<string.h>
#include<stdio.h>
#include<set>
using namespace std;
set<int> pos;
const int maxn=1000100;
char s[2][maxn];//存两个字符串
int n,m,len,len1,len2;
int main()
{
int com,a,b,t,q,i,cas=1;
char c[100];
scanf("%d",&t);
while(t--)
{
printf("Case %d:\n",cas++);
scanf("%s%s",s[0],s[1]);
pos.clear();
len1=strlen(s[0]);
len2=strlen(s[1]);
len=max(len1,len2);
pos.insert(len);
for(i=0;i<len;i++)
if(s[0][i]!=s[1][i])
pos.insert(i);
scanf("%d",&q);
while(q--)
{
scanf("%d",&com);
if(com==1)
{
scanf("%d%d%s",&a,&b,c);
a--;
if(s[a][b]==s[a^1][b]&&c[0]!=s[a][b])
pos.insert(b);
else if(s[a][b]!=s[a^1][b]&&c[0]==s[a^1][b])
pos.erase(b);
s[a][b]=c[0];
}
else
{
scanf("%d",&a);
if(s[0][a]!=s[1][a])
{
printf("0\n");
continue;
}
printf("%d\n",*pos.lower_bound(a)-a);
}
}
}
return 0;
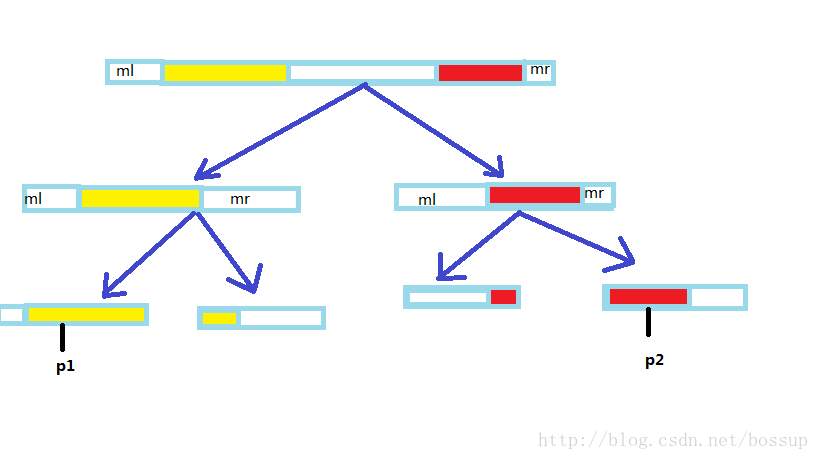
}第二种方法要复杂一点。但要高效许多。用到的是线段树区间维护。对于线段树的一个结点。维护两个信息。
ml,mr。分别表示该结点所代表区间中。
ml从区间左端点开始算起有多少连续个字符匹配。
mr从区间右端点开始算起有多少连续个字符匹配。
要得到这两个信息很简单,直接从叶子结点往上更新。
ls为左儿子的下标。rs为右儿子的下标。
k为当前结点的下标。
L,R为当前区间的左右端点。
那么递归更新式就为:
ml[k]=ml[ls];
mr[k]=mr[rs];
if(ml[ls]==mid-L+1)//左区间满了可以和右区间连在一起
ml[k]+=ml[rs];
if(mr[rs]==R-mid)//右区间满了。
mr[k]+=mr[ls];
怎么从维护的这两个信息得到答案呢?
对于更新操作很简单。如果状态改变了。直接从叶子结点往上更新就行了。
对于询问。假设询问的位置为pos。那么pos的位置有3中可能。
1.在右连续的区间内即[R-mr[k]+1,R]。
2.在左连续的区间内即[L,L+ml[k]-1]。
3.在这两区间中间。
这三种情况依次判断
对于第一种情况。(如图p1)
ans+=R-pos+1。并且要标记下。因为右连续的话有可能与右边的区间连续。到父结点时要ans+=ml[ls]。
对于第二种情况。(如图p2)
答案是确定的。ans=L+ml[k]-pos。因为第一种情况不成立才会判断第二种情况。说明pos后面位置至少有一个不匹配。所以ans=L+ml[k]-pos。
对于第三种情况。继续往下询问就行了。因为迟早会出现1,2.两种情况。
详细见代码:
#include <iostream>
#include<string.h>
#include<stdio.h>
using namespace std;
const int maxn=1000100;
int ml[maxn<<2],mr[maxn<<2];//左连续。右连续的值
char s[2][maxn];//存两个字符串
int n,m,len,ans,flag,len1,len2;
void btree(int L,int R,int k)//建树
{
int ls,rs,mid;
if(L==R)
{
if(s[0][L]==s[1][L])
ml[k]=mr[k]=1;
else
ml[k]=mr[k]=0;
return;
}
ls=k<<1;
rs=k<<1|1;
mid=(L+R)>>1;
btree(L,mid,ls);
btree(mid+1,R,rs);
ml[k]=ml[ls];
mr[k]=mr[rs];
if(ml[ls]==mid-L+1)//若右区间全满
ml[k]+=ml[rs];//可能变成的值
if(mr[rs]==R-mid)
mr[k]+=mr[ls];
}
void update(int L,int R,int x,int k)//更新x点
{
int ls,rs,mid;
if(L==R)
{
if(s[0][L]==s[1][L])
ml[k]=mr[k]=1;
else
ml[k]=mr[k]=0;
return;
}
ls=k<<1;
rs=k<<1|1;
mid=(L+R)>>1;
if(x>mid)
update(mid+1,R,x,rs);
else
update(L,mid,x,ls);
ml[k]=ml[ls];
mr[k]=mr[rs];
if(ml[ls]==mid-L+1)
ml[k]+=ml[rs];
if(mr[rs]==R-mid)
mr[k]+=mr[ls];
}
void qu(int L,int R,int k,int pos)//询问pos前有多少相同字符(包括pos)
{
int ls,rs,mid;
if(L==R)
{
ans+=ml[k];
return;
}
ls=k<<1;
rs=k<<1|1;
mid=(L+R)>>1;
if(R-pos+1<=mr[k])//在右连续区间内
{
ans+=R-pos+1;
flag=1;//如果是左儿子才标记的但是。右儿子不会出现这种情况。因为点右连续区间内在父结点处就返回了。所以可以直接加标记
return;
}
if(pos-L+1<=ml[k])//在左连续区间内
{
ans=L+ml[k]-pos;
return;
}
if(pos>mid)
qu(mid+1,R,rs,pos);
else
qu(L,mid,ls,pos);
if(flag)//加上延长的区间
{
ans+=ml[rs];
flag=0;
}
}
int main()
{
int com,a,b,t,q,cas=1;
char c[100],temp;
scanf("%d",&t);
while(t--)
{
printf("Case %d:\n",cas++);
scanf("%s%s",s[0]+1,s[1]+1);//字符从一开始了方便建树
len1=strlen(s[0]+1);
len2=strlen(s[1]+1);
len=max(len1,len2);//以较大的建树。开始以小的建树RE了。。TT
btree(1,len,1);
scanf("%d",&q);
while(q--)
{
scanf("%d",&com);
if(com==1)
{
scanf("%d%d%s",&a,&b,c);
a--;//2->1,1->0
b++;//由于从1开始所以要挪一下
temp=s[a][b];
s[a][b]=c[0];
if(temp==s[a^1][b]&&c[0]!=temp)
update(1,len,b,1);
else if(temp!=s[a^1][b]&&c[0]==s[a^1][b])
update(1,len,b,1);
}
else
{
scanf("%d",&a);
a++;
if(s[0][a]!=s[1][a])
{
printf("0\n");
continue;
}
flag=0;
ans=0;
qu(1,len,1,a);
printf("%d\n",ans);
}
}
}
return 0;
}感想:做题需要的就是思维,而现在思维还不够活跃。还需要好好加油啊!






















 1405
1405

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








