深度学习系统学习系列【2】之人工神经网络（ANN）

说明

• 文章属于个人学习笔记内容，仅供学习和交流。
• 内容参考深度学习原理与实践》陈仲铭版和个人学习经历和收获而来。

人工神经网络概述

• 人工神经网络(Artifical Neural Network, ANN ）是深度学习的基础。人工神经网络是深度神经网络中最经典，也是最基础的网络模型
• 人工神经网络以其独特的网络结构和处理信息的方法，在自动控制领域、组合优化问题、模式识别、图像处理、自然语言处理等诸多领域，己经取得了辉煌的成绩。

基本单位（神经元模型）

• 人工神经网络是生物神经网络的一种模拟和近似。它从结构、实现机理和功能上模拟生物神经网络。
• 模拟生物神经元模型的人工神经元模型示例图
  
• 神经元的输入$x_i$对应生物神经元的树突。输入$x_i$向细胞体传播脉冲，相当于输入权值参数$w_i$，通过细胞核对输入的数据和权值参数进行加权求和。
• 传播细胞体的脉冲相当于人工神经元的激活函数，最终输出结果$y$作为下一个神经元的输入。

---

• 人工神经网络中最基本的处理单元——神经元，主要由连接、求和节点、激活函数组成。
  • 连接（Connection）： 神经元中数据流动的表达方式。
  • 求和结点（Summation Node）：对输入信号和权值的乘积进行求和。
  • 激活函数（Activate Function）： 一个非线性函数，对输出信号进行控制。

神经元基本模型

• 神经元的数学基本表达式
  $$\begin{array}{rl}y& =f(\sum _{i=1}^n{w}_i{x}_i+b)\\ & =f(W^{T}X+b)\end{array}$$
• $W=[w_1,w_2,...,w_n]为权值向量，X=[x-1,x_2,...,x_n]为输入向量$

• $x_1,x_2,...,x_n$为输入信号的各个分量.
• $w_1,w_2,...,w_n$为神经元各个突触的权值。
• b为神经元的偏置参数。
• $\sum$为求和节点，$z=x_1{w}_1+x_2{w}_2+...+x-n{w}_n+b={\sum }_{i=1}^n{w}_i{x}_i+b$
• $f$为激活函数， 一般为非线性函数，如Sigmoid、 Tanh 函数等；
• $y$为该神经元的输出。

线性模型与激活函数

• 线性回归模型和分类模型本质上都是将数据进行映射，既可以映射到一个或多个离散的标签上，也可以映射到连续的空间。
• 单个神经元模型在没有加入激活函数时，就是一个线性回归模型，可以把输入的数据映射到一个$n$维的平面空间中。
• 神经元加入一个非线性函数（激活函数），相当与在神经元中加入非线性因素，使神经元模型更好地解决复杂的数据分布问题。
  
• 神经元模型不仅可以看作对生物神经元的模拟，而且能够有效处理数学中的非线性数据理。理论上，由多个神经元组合而成的神经网络可以表示成任何复杂的函数。

多层神经网络

• 人工神经网络由多个神经元组合而成，神经元组成的信息处理网络具有并行分布式结构。
• 一个人工神经网络中的每一层的神经元都拥有输入和输出，每一层都是由多个神经元组成。第$l-1$层网络神经元的输出是第$l$层神经元的输入，输入的数据通过神经元上的激活函数来控制输出数值的大小。该输出数值是 一个非线性值，通过激活函数求得数值，根据极限值来判断是否需要激活该神经元。
• 多层人工神经网络（ANN）由输入层、输出层和隐藏层组成。
  • 输入层（InputLayer）：接收输入信号作为输入层的输入。
  • 隐藏层（Hidden Layer/隐层）：它介于输入层和输出层之间，是由大量神经元井列组成的网络层，通常一个人工神经网络可以有多个隐层。
  • 输出层（Output Layer）：信号在神经网络中经过神经元的传输、内积、 激活后，形成输出信号进行输出。
    
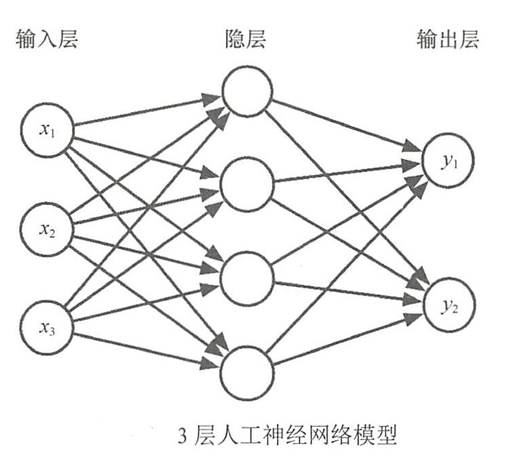
• 如上图，输入层为3 个元素组成的一维向量，隐层有4个节点，因此从输入层到隐层共有 $3\times 4=12$条连接线；输出层是由 $2$个元素组成的一维向量，因此从隐层到输出层共有$4\times 2=8$ 条连接线。

人工神经网络的注意内容

• 人工神经网络输入层与输出层的节点数往往是固定的，根据数据本身而设定，隐层数和隐层节点则可以自由指定。
• 人工神经网络模型图中的箭头代表预测过程时数据的流向，与学习训练阶段的数据流动方向不同。
• 人工神经网络的关键不是节点而是连接，每层神经元与下一层的多个神经元相连接，每条连接线都有独自的权重参数。连接线上的权重参数是通过训练得到的。
• 人工神经网络中不同层的节点间使用全连接的方式， 也就是$l-1$层的所有节点对于$l$层的所有节点都会有相互连接。例如当前层有3个节点，下一层4 个节点，那么连接线有$3\times 4=12$条，共 $12$个权重值和$4$个偏置。

人工神经网络的阶段划分

• 深度学习的一般方法分为训练与预测阶段。在训练阶段，准备好原始数据和与之对应的分类标签数据，通过训练得到模型$Ⅰ$。在预测阶段，对新的数据套用该模型$Ⅰ$，可以预测新输入数据的类别。

训练阶段

输入、输出数据量化的设计

• 在设计人工神经网络模型结构前，我们需要对输入和输出的数据进行量化。假设输入的一条数据的维度（特征）维度为$k$，输出为$n$个分类，那么输入层的神经元节点数应设置为$k$，输出层的神经元节点数应设置为$n$。

---

1. 输入层的神经元节点数（k）

• 含义：输入层的神经元数量应与每条数据的特征维度一致。

• 例如，若输入是图像（如28×28像素的灰度图），展平后每条数据是一个784维的向量（28×28=784），则输入层需要784个神经元；若输入是表格数据（如年龄、身高、体重等3个特征），则输入层需要3个神经元。

• 为什么不是样本数量（N）？ 样本数量（即数据条数）决定训练时的批量大小（batch size），但不会影响网络结构。网络每次处理一条数据时，只关注该数据的特征维度（k）。

---

2. 输出层的神经元节点数（n）

• 含义：输出层的神经元数量应与分类任务的类别数一致。
• 例如，手写数字识别（MNIST）有10类（0~9），输出层需要10个神经元；二分类任务（如猫狗分类）通常用1个神经元（通过sigmoid输出概率）或2个神经元（softmax多分类形式）。

---

• 任务：鸢尾花分类（4个特征：花萼长/宽、花瓣长/宽；3个类别：山鸢尾、杂色鸢尾、维吉尼亚鸢尾）。
  • 输入层：4个神经元（对应4个特征）。
  • 输出层：3个神经元（对应3个类别，使用softmax激活）。
  • 样本数量：假设有150条数据（N=150），但网络结构不受此影响。

---

权值向量W和偏置b的设计

• 人工神经网络的训练实际上是通过算法不断修改权值向量W和偏置b，使其尽可能与真实的模型逼近，以使得整个神经网络的预测效果最佳。
• 操作步骤：首先给所有权值向量 W和偏置b赋予随机值，使用这些随机生成的权重参数值来预测训练、数据中的样本。样本的预测值为$\hat{y}$，真实值为y。定义一个损失函数，目标是使预测值$\hat{y}$尽可能接近于真实值y，损失函数就是使神经网络的损失值和尽可能小。其基本公式为：
  $$lossfuntion=(\hat{y}-y{)}^2$$
• 如何改变神经网络中的参数$W$和$b$，让损失函数的值最小？
• 实现优化的关键技术=梯度下降 + 反向传播。

1. 目标：调整参数（W, b），使损失函数值最小 → 转化为优化问题。
2. 方法：
   • 梯度下降：沿梯度方向更新参数，逐步降低损失。
   • 反向传播：高效计算网络中所有参数的梯度（通过链式法则）。
3. 流程： 反向传播求出梯度 → 梯度下降更新参数 → 迭代直至损失收敛。

• 当损失函数收敛到一定程度时结束训练，保存训练后神经网络的参数。

预测阶段

• 完成人工神经网络的训练阶段后，使用保存的参数，将向量化后的预测数据从人工神经网络的输入层开始输入，顺着数据流动的方向在网络中进行计算，直到数据传输到输出层并输出 （一次向前传播〉，就完成一次预测并得到分类结果。

人工神经网络核心算法

• 人工神经网络的三大核心算法（梯度下降算法、向前传播算法、反向传播算法）。
• 神经网络在训练和预测阶段都需要频繁使用向前传播算法，而在训练阶段则多次用到梯度下降算法和反向传播算法。

梯度下降算法

• 梯度下降算法（Gradient Descent）

向前传播算法

• 向前传播（Feed Forward）算法在神经网络的训练和预测阶段会被反复使用，是神经网络中最常见的算法。只需要根据神经网络模型的数据流动方向对输入的数据进行计算，最终得到输出的结果。

---

• 人工神经网络模型，其输入层有2个节点，隐层、输出层均有3个节点。
• 假设$z_i^l$为第$l$层网络第$i$个神经元的输入，$w_{i,j}^l$为第$l$层网络第$i$个神经元到第$l+1$层网络中第$j$个神经元的连接。
  $$z_i^l=\sum j=1w_{i,j}^l{x}_i+b_i$$

$$W=\left[\begin{array}{ccc}{w}_{1,1}& w_{1,2}& w_{1,3}\\ w_{2,1}& w_{2,2}& w_{2,3}\end{array}\right],X=\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right],B=\left[\begin{array}{c}{b}_1\\ b_2\\ b_3\end{array}\right]$$

$$\begin{array}{rl}{W}^{T}X+B& =\left[\begin{array}{cc}{w}_{1,1}& w_{2,1}\\ w_{1,2}& w_{2,2}\\ w_{1,3}& w_{2,3}\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]+\left[\begin{array}{c}{b}_1\\ b_2\\ b_3\end{array}\right]\\ & =\left[\begin{array}{c}{w}_{1,1}{x}_1+w_{2,1}{x}_2\\ w_{1,2}{x}_1+w_{2,2}{x}_2\\ w_{1,3}{x}_1+w_{2,3}{x}_2\end{array}\right]+\left[\begin{array}{c}{b}_1\\ b_2\\ b_3\end{array}\right]\\ & =\left[\begin{array}{c}\sum _{i=1}^2{w}_{i,1}{x}_i+b_1\\ \sum _{i=1}^2{w}_{i,2}{x}_i+b_2\\ \sum _{i=1}^2{w}_{i,3}{x}_i+b_3\end{array}\right]\\ & =\left[\begin{array}{c}{z}_1\\ z_2\\ z_3\end{array}\right]\end{array}$$

• 单层神经网络的向前传播算法可以使用矩阵表达为
  $$\begin{gathered} a^{(l)}=f(w^{T}x+b) \\ f为激活函数，a^{(l)}第l层网络的输出矩阵 \end{gathered}$$

def feedForward （intput a, weight, bias) : 
	f = lambda x :l./(l.+np.exp (-x)) ＃使用 Sigmod 函数作为激活函数
	return f(np.dot(weight, intput a) +bias) 

反向传播算法（Back Propagation）

• 反向传播算法（BP）的提出是为了高效计算神经网络中每个参数的梯度。由于神经网络多层堆叠的结构特点，参数变化会逐层传递并最终影响损失函数。BP算法通过从输出层反向传播误差，利用链式求导法则逐层计算每个参数的梯度。
  
• 相比其他梯度计算方法，BP算法虽然存在收敛慢、易陷局部最优等缺点，但其计算精度和实用性更优，因此成为现代神经网络训练的主流方法。
• 算法核心思想是：通过计算图跟踪参数，利用链式求导计算损失函数对每个参数（权重w和偏置b）的偏导数$\partial L/\partial w$和$\partial L/\partial b$。
• 举例说明：类似"传话绘画"游戏，正向传播逐层传递信息产生误差，反向传播则将误差从输出层逐层回传，指导各层参数调整。这种反向误差传播机制正是BP算法的精髓所在。

计算图

• 计算图可以看作一种用来描述计算函数的语言，图中的节点代表函数的操作，边代表函数的输入。

• $f(x,y,z)=(x+y)z$的计算图为：
  

• 反向传播算法希望通过链式法则得到f的各个参数的梯度：$\partial f/\partial z,\partial f/\partial x,\partial f/\partial y$

• 假设$q=x+y$，则$f=qz=(x+y)z$，当$x=-5,y=2,z=-6$
  $$\begin{gathered} \frac{\partial f}{\partial z}=q=-3 \\ \frac{\partial f}{\partial x}=\frac{\partial f}{\partial q}\frac{\partial q}{\partial x}=z=-6 \\ \frac{\partial f}{\partial y}=\frac{\partial f}{\partial q}\frac{\partial q}{\partial y}=z=-6 \end{gathered}$$

BP 算法

• $n_l$：表示网络的层数，$n_1$为输入层， $n_l$为输出层。
• $s_l$：表示第$l$层网络神经元的个数。
• $f$：表示神经元的激活函数。
• $w_l$:表示第$l$层到第$l+1$层的权重矩阵，$w_{(i,j)}^l\in R$表示从$l$层的第$i$个神经元第$l+1$层第$j$个神经元之间的权重。
• $b^{(l)}$：表示第$l$层的偏置向量，其中$b_i^{(l)}$表示$l$层第$i$个神经元的偏置。
• $z^{(l)}$：表示第l层的输入向量。中$z_i^{(l)}$为$l$层第$i$个神经元的输入。
• $a^l$：：表示第$l$层的输出向量，其中$a_i^{(l)}$为$l$层第$i$个神经元的输出。

---

• 当前层神经网络的向前传播公式
  $$a^l=f(z^i)=f(w^{l-1}{a}^{l-1}+b^l)$$
• 损失函数
  $$\begin{gathered} L(w,b)=\frac{1}{2}(y-a^L{)}^2 \\ y为期望的输出值，a^L为该神经网络的预测输出值，上标L为网络的最后一层（输出层） \end{gathered}$$
• 反向传播算法是通过改变网络中的权重参数w和偏置b来改变损失函数的方法，目的是计算损失函数L在神经网络中的所有权重w，以及偏置b的梯度$\partial L/\partial w$和$\partial L/\partial b$
• 反向传播的4个基本方程
  • 定义第$l$层的第$i$个神经元的误差为$${\delta }_i^l=\frac{\partial L}{\partial z_i^l}$$
    

方程	含义
${\delta }^L={\nabla }_{a}L\odot f^{\prime }(z^L)$	BP1 输出层误差
${\delta }^l=((w^l{)}^T{\delta }^{l+1})\odot f^{\prime }(z^l)$	BP2 第 $l$ 层误差
$\frac{\partial L}{\partial b_i^l}={\delta }_i^l$	BP3 损失函数关于偏置的偏导
$\frac{\partial L}{\partial w_{i,j}^l}=a_j^{l-1}{\delta }_i^l$	BP4 损失函数关于权值的偏导

反向传播算法流程

1. 输入 (lnput）：输入层输入向量x。
2. 向前传播 （Feed Forward）：计算$z^l=w^{l-1}{a}^{l-1}+b^l,a^l=f(z^l)$。
3. 输出层误差 （Output Error）：根据公式BP1 计算误差向量${\delta }^L={\nabla }_{a}L\odot f^{\prime }(z^L)$
4. 反向传播误差 （Backpropagate Error）：根据公式 BP2 逐层反向计算每一层的误差${\delta }^l=((w^l{)}^T{\delta }^{l+1})\odot f^{\prime }(z^l)$
5. 输出 （Output）：根据公式BP3 和 BP4 输出损失函数的偏置

反向传播算法的实现

• 在实现反向传播算法之前，需要定义神经网络的模型架构，即神经网络有多少层、每一层有多少神经元。还需要给出神经网络定义训练的数据和实际的输出。
• 示例代码： network sizes 为用于测试的神经网络的模型架构，该网络一共有3层，输入层有3个神经元，隐层有4个神经元，输出层有2个神经元。

import numpy as np

# 定义神经网络的模型架构 [input, hidden, output]
network_sizes = [3, 4, 2]

# 初始化该神经网络的参数
sizes = network_sizes
num_layers = len(sizes)
biases = [np.random.randn(h, 1) for h in sizes[1:]]  # 每层的偏置（从第2层开始）
weights = [np.random.randn(y, x) for x, y in zip(sizes[:-1], sizes[1:])]  # 权重矩阵

# 产生训练数据
training_x = np.random.rand(3).reshape(3, 1)  # 输入数据 (3维)
training_y = np.array([0, 1]).reshape(2, 1)  # 期望输出 (2维)

print("training data x: {}, training data y: {}\n".format(training_x, training_y))


# 定义损失函数和激活函数、激活函数的求导
def loss_der(network_y, real_y):
    '''
    返回损失函数的偏导，损失函数使用 MSE
     L = 1/2(network_y-real_y)^2
    delta_l = network_y-real_y
    '''
    return network_y - real_y


def sigmoid(z):
    '''
    返回Sigmoid函数的值
    '''
    return 1.0 / (1.0 + np.exp(-z))


def sigmoid_der(z):
    '''
    返回Sigmoid函数的导数
    '''
    return sigmoid(z) * (1 - sigmoid(z))


# 反向传播函数
def backprop(x, y):
    # 1 初始化网络参数的导数权重w的偏导和偏置b的偏导
    delta_w = [np.zeros(w.shape) for w in weights]
    delta_b = [np.zeros(b.shape) for b in biases]

    # 2 计算网络输出 (前向传播)
    activation = x  # 把输入的数据作为第一次激活值
    activations = [x]  # 激活值列表
    zs = []  # 存储网络的加权输入值 （z=wx+b)
    for w, b in zip(weights, biases):
        z = np.dot(w, activation) + b
        activation = sigmoid(z)
        activations.append(activation)
        zs.append(z)

    # 反向传播
    # BP1 计算输出层误差
    delta_l = loss_der(activations[-1], y) * sigmoid_der(zs[-1])
    # BP3 损失函数在输出层关于偏置的偏导
    delta_b[-1] = delta_l
    # BP4 损失函数在输出层关于权值的偏导
    delta_w[-1] = np.dot(delta_l, activations[-2].transpose())

    delta_l2 = delta_l
    for l in range(2, num_layers):
        # BP2 计算隐藏层误差
        delta_l2 = np.dot(weights[-l + 1].transpose(), delta_l2) * sigmoid_der(zs[-l])
        # BP3 损失函数在隐藏层关于偏置的偏导
        delta_b[-l] = delta_l2
        # BP4 损失函数在隐藏层关于权值的偏导
        delta_w[-l] = np.dot(delta_l2, activations[-l - 1].transpose())

    return delta_w, delta_b