数据建模与分析：从回归预测到特征聚类的全面探索（PyTorch）

简介：

• 在现代数据科学中，数据建模是分析和理解复杂数据的重要工具。无论是预测未来趋势还是从数据中提取潜在模式，数据建模都发挥着关键作用。本文将带您走进数据建模的世界，首先介绍回归分析，这一经典的统计方法，展示其在实际问题中的建模过程，如住房价格的回归预测。接着，我们将探讨聚类分析，了解如何将相似的数据点分组，尤其是在植物花卉特征的研究中。最后，我们将深入分析主成分分析（PCA），探讨其在降维和数据简化中的应用，特别是在地区竞争力指标的分析上。通过这些内容，您将能够更好地掌握数据建模的核心概念，为您的数据分析技能打下坚实的基础。

数据建模简介

• 数据建模（数据挖掘），是一种从大量数值型数据中寻找规律的技术。它通常包括3个步骤：数据准备、规律寻找和规律表示。
  • 数据准备是从相关的数据源中选取所需的数据并整合成用于数据挖掘的数据集
  • 规律寻找是用某种方法将数据集所含的规律找出来
  • 规律表示是尽可能以用户可理解的方式将找出的规律表示出来。

回归分析

• 回归分析是研究一个变量（被解释变量）与另外一个或几个变量（解释变量）的具体依赖关系的计算方法和理论。

回归分析简介

• 回归分析是一种统计方法，用于探究变量间的数学关系、评估关系可信度，并利用模型进行预测或控制。
• 线性回归主要用来解决连续数值预测问题。例如，关于吸烟对死亡率和发病率影响的证据来自采用回归分析方法的观察性研究。

回归分析建模

• 线性回归（Linear Regression）就是利用回归方程对一个或多个变量和因变量之间的关系进行建模的一种分析方式。只有一个自变量的情况称为一元回归，大于一个自变量的情况称为多元回归。多元回归模型公式如下：
  $$y={\beta }_0+{\beta }_1{x}_1+{\beta }_2{x}_2+\cdots +{\beta }_k{x}_k+\epsilon$$
• $x_1,x_2,...,x_3$是自变量，${\beta }_0$是截距，${\beta }_1,...,{\beta }_k$是变量回归系数，$\epsilon$是误差项的随机变量。
• 为使预测尽量准确，让真实值与预测值的差值最小，也就是让误差平方和最小，用公式来表达如下
  $$\begin{array}{r}J(\beta )=\sum {\left(y-X\beta \right)}^2\end{array}$$
• 在线性回归模型中，求解损失函数就是求与自变量相对应的各个回归系数和截距。对于误差平方和损失函数的求解方法有很多，典型的是最小二乘法，梯度下降。
  • 最小二乘法的特点：步骤简单，一步到位，直接求的全局最优解。
  • 梯度下降法的特点：间接求解，依次迭代，局部求解。既可以求的线性模型，也可以用于非线性模型，没有特殊的限制和假设条件。

判定系数

• 回归直线与各观测点的接近程度就是回归直线对数据的拟合优度，而评判直线拟合优度需要一些指标，其中一个就是判定系数。
• 因变量y的值来自两个方面：自$x$值的影响(预测的主要依据)；干扰项$\epsilon$的影响
• 如果要让一个回归直线预测准确，就需要让$x$的影响尽可能大，让干扰项的影响尽可能小，也就是说$x$影响占比越高，预测效果就越好。可以采用平方和（SSD），回归平方和（SSR），残差平方和（SSE）进行预测效果的判断。
  $$\begin{array}{l}\mathrm{SST}=\sum {\left(y_i-\overline{y}\right)}^2\\ \mathrm{SSR}=\sum {\left(y_i-\overline{y}\right)}^2\\ \mathrm{SSE}=\sum {\left(y_i-\hat{y}\right)}^2\end{array}$$
• SST（总平方和）：误差的总平方和。
• SSR（回归平方和）：由$x$与$y$之间的线性关系引起的y变化，反映了回归值的分散程度。
• SSE（残差平方和）：除$x$影响外的其他因素引起的$y$变化，反映了观测值偏离回归直线的程度。
• SST、SSR、SSE三者之间的关系如图所示：SSR越高，则代表回归预测越准确，观测点越靠近直线，即越大，直线拟合越好。判定系数的定义就自然地引出来，一般称为$R^2$。
  $$R^2=\frac{SSR}{SST}=1-\frac{SSE}{SST}$$
  

估计标准差

• 判定系数R²的意义是由$x$引起的影响占总影响的比例来判断拟合程度。也可以从误差的角度来评估，也就是用残差$SSE$进行判断。估计标准误差$S$。是均方残差的平方根，度量实际观测点在直线周围散布的情况。
  $$S_{\epsilon }=\sqrt{\frac{\mathrm{SSE}}{n-2}}=\sqrt{\mathrm{MSE}}$$
• 估计标准误差与判定系数相反，$S_{\epsilon }$反映预测值与真实值之间误差的大小。误差越小，就说明拟合度越高；相反，误差越大，就说明拟合度越低。

住房价格回归预测

1. 利用深度学习的方法对某地的房价进行预测，销售者根据预测结果选择适合自己的房屋。
2. 考虑住房价格影响因素，如房屋的面积、户型、类型、配置设施、地理位置

字段名称	字段说明
Id	住房编号
Area	房屋面积
Shape	房屋户型
Style	房屋类型
Utilties	配套设施，如通不通水电气
Neighborhood	地理位置
Price	销售价格

# 导入相关第三方库
import torch
import numpy as np
import pandas as pd
from torch.utils.data import DataLoader,TensorDataset
import time
start=time.perf_counter()

# 1 读取训练数据和测试数据
train_data=pd.read_csv('./train.csv')
test_data=pd.read_csv('./test.csv')

# 2 合并数据集
## 合并train_data和test_data数据的Area到Neighborhood列
all_features = pd.concat((train_data.loc[:,'Area':'Neighborhood'],test_data.loc[:,'Area':'Neighborhood']))
## 合并train_data和test_data的Price列
all_labels = pd.concat((train_data.loc[:,'Price'],test_data.loc[:,'Price']))

# 3 数据预处理
# 提取所有特征中数据类型的特征索引
numeric_feats=all_features.dtypes[all_features.dtypes!="object"].index
# 提取所有特征中对象类型的特征索引
object_feats=all_features.dtypes[all_features.dtypes=="object"].index
# 数据类型特征标准化处理
all_features[numeric_feats]=all_features[numeric_feats].apply(lambda x: (x-x.mean())/(x.std()))
# 对对象类型的特征进行独热编码
all_features=pd.get_dummies(all_features,columns=object_feats,dummy_na=True)
# 用所有特征的均值填充缺失值
all_features=all_features.fillna(all_features.mean())

# 4 对标签进行数据预处理
# 对标签进行 z-score 标准化
mean = all_labels.mean()
std = all_labels.std()
all_labels = (all_labels - mean)/std

num_train = train_data.shape[0]
train_features = all_features[:num_train].values.astype(np.float32) #(1314, 331)
test_features = all_features[num_train:].values.astype(np.float32)# (146, 331)
train_labels = all_labels[:num_train].values.astype(np.float32)
test_labels = all_labels[num_train:].values.astype(np.float32)
#输入数据准备完毕 经过one-hot编码后  特征维度增加 81->331

#数据类型转换，数组转换成张量
train_features = torch.from_numpy(train_features)
train_labels = torch.from_numpy(train_labels).unsqueeze(1)
test_features = torch.from_numpy(test_features)
test_labels = torch.from_numpy(test_labels).unsqueeze(1)
train_set = TensorDataset(train_features,train_labels)
test_set = TensorDataset(test_features,test_labels)

#设置迭代器
# 创建一个数据加载器train_data，用于加载训练数据。数据集使用train_set，批大小设置为 64，并且数据会被打乱（shuffle=True）
train_data = DataLoader(dataset=train_set,batch_size=64,shuffle=True)
# 创建另一个数据加载器test_data，用于加载测试数据。数据集使用test_set，批大小同样为64，但数据不会被打乱（shuffle=False）
test_data  = DataLoader(dataset=test_set,batch_size=64,shuffle=False)

# 设置网络结构
class Net(torch.nn.Module):# 继承 torch 的 Module
    def __init__(self, n_feature, n_output):
        super(Net, self).__init__()
        # 定义第一层 全链接层 输入特征数为n_feature 输出维度为600
        self.layer1 = torch.nn.Linear(n_feature, 600)
        # 定义 第二层 全链接层 输入特征数为600 输出维度为1200
        self.layer2 = torch.nn.Linear(600, 1200)
        # 定义 第三层 全连接层 输入维度1200 输出目标数 n_output
        self.layer3 = torch.nn.Linear(1200, n_output)
    # 定义前向传播
    def forward(self, x):
        x = self.layer1(x)
        x = torch.relu(x)
        x = self.layer2(x)
        x = torch.relu(x)
        x = self.layer3(x)
        return x

# 定义Net实例,输入特征数为44，输出目标数为1
net = Net(44,1)

# 定义损失函数和优化器
# 使用均方误差作为损失函数，使用Adam优化器，学习率设为0.01
optimizer = torch.optim.Adam(net.parameters(), lr=1e-4)
loss_func = torch.nn.MSELoss()

# 存储训练损失的列表
losses=[]
# 用于存储评估损失的列表
eval_losses=[]
# 进行1000次迭代训练
for epoch in range(1000):
    train_loss=0 # 训练损失的累计值
    net.train()  # 训练模式
    for t_data,t_label in train_data: # 迭代训练数据
        pred = net(t_data)            # 预测结果
        loss= loss_func(pred, t_label) # 计算损失
        optimizer.zero_grad()         # 梯度清零
        loss.backward()               # 反向传播
        optimizer.step()              # 更新参数
        train_loss+=loss.item()       # 累计损失

    # 将训练损失添加到列表中
    losses.append(train_loss/len(train_data))

    eval_loss=0  # 评估损失的累计值
    net.eval()   # 评估模式
    for e_data,e_label in test_data:
        pred = net(e_data) # 预测结果
        loss = loss_func(pred, e_label) # 计算损失
        eval_loss+=loss.item() # 累计损失
    eval_losses.append(eval_loss/len(test_data)) #  将评估损失添加到列表中
    # 打印训练次数、训练集损失和测试集损失
    print('训练次数:',epoch,'训练集损失:',train_loss/len(train_data),'测试集损失:',eval_loss/len(test_data))

# 模型评估与预测
pred=net(test_features) # 对测试特征进行网络向前传播
y_pred=pred*std+mean # 预测值标准化处理
print('测试集预测值：',y_pred.squeeze().detach().cpu().numpy())
print('模型平均误差：',abs(y_pred - (test_labels*std + mean)).mean().cpu().item() )

end =time.perf_counter()
print('模型运行时间：',end-start)

测试集预测值： [12301.136 15382.906 21838.062 14276.917 17254.664 12320.577 13342.348
 10531.165 28399.271]
模型平均误差： 5159.6943359375
模型运行时间： 104.9702648

聚类

• 聚类分析是一种探索性的分析，在分类时，不必事先给出一个分类的标准，聚类分析能够从样本数据出发，自动进行分类。

聚类简介

• 聚类分析是根据事物本身的特性研究个体的一种方法，目的在于将相似的事物归类。它的原则是同一类中的个体有较大的相似性，不同类别之间的个体差异性很大。
• 聚类算法往往具有以下特征：
  1. 适用于没有先验知识的分类。
  2. 可以处理多个变量决定的分类。如根据消费者的购买量，家庭收入，家庭支出，年龄等多个指标进行分类。
  3. 是一种探索分析方法，能够分析事务内在特点和规律，并根据相似性原则对事务进行分组。

聚类分析建模

• 一般情况下，聚类分析的建模步骤为：$数据预处理\to 定义衡量相似度的距离函数\to 聚类或分组\to 评估输出$。

1. 数据预处理包括选择择数量，类型和特征的标度，主要依靠特征选择和特征抽取。数据预处理还包括移除孤立数据，减少聚类结果偏差。
   • 特征选择是选择重要的特征。
   • 特征抽取是将输入的特征转化为一个新的显著特征，经常用来获取一个合适的特征集来避免“维数灾”进行聚类。

• 维数灾的定义：维数灾（Curse of Dimensionality）是指在高维空间中，数据分析和机器学习算法面临的一系列问题。随着维度的增加，数据的稀疏性急剧增加，导致许多传统方法在高维空间中失效。
• 维数灾的表现：在高维空间中，数据点之间的距离变得非常相似，导致基于距离的算法（如K近邻）难以区分不同的数据点。高维空间中的体积增长迅速，使得数据分布变得极其稀疏，难以捕捉有效的模式。
• 维数灾的影响：维数灾会导致模型过拟合，因为在高维空间中，模型可能会捕捉到噪声而非真实的模式。计算复杂度也会显著增加，因为处理高维数据需要更多的计算资源。

2. 为衡量数据点间相似度定义距离函数

   • 聚类算法的核心是将相似的数据归为一类。因此，如何衡量数据之间的相似度非常关键。由于数据的特征类型和取值范围各不相同，我们需要根据实际情况选择合适的距离计算方法。例如，欧氏距离（两点间的直线距离）就是一种常用的相似度衡量标准，适用于很多场景。不同的应用场景可能需要采用不同的距离计算方式。
   • 常用来衡量数据点间的相似度的距离有海明距离、欧氏距离、马氏距离，公式如下：
     $$海明距离：d(x_i,x_j)=\sum _{k=1}^m|x_{ik}=x_{jk}|$$
     $$欧式距离：d(x_i,x_j)=\sqrt{\sum _{k=1}^m(x_{ik}-x_{jk}{)}^2}$$
     $$马氏距离：d(x_i,x_j)=\sqrt{(x_i-x_j{)}^T{\Sigma }^{-1}(x_i-x_j)}$$

3. 聚类或分组

• 划分方法和层次方法是聚类分析的两个主要方法。划分方法一般从初始划分和最优化一个聚类标准开始，主要方法包括：
  • Crisp Clustering：它的每个数据都属于单独的类。
  • FuzzyClustering：它的每个数据都可能在任何一个类中。
• Crisp Clustering和FuzzyClustering是划分方法的两个主要技术，划分方法聚类是基于某个标准产生一个嵌套的划分系列，它可以度量不同类之间的相似性或一个类的可分离性，用来合并和分裂类。其他的聚类方法还包括基于密度的聚类、基于模型的聚类、基于网格的聚类。

4. 评估输出

• 聚类是无管理程序，没有客观的标准来评价聚类结果，只能通过一个类的有效索引来评价。一般来说，几何性质，包括类之间的分离和类自身内部的耦合一般都用来评价聚类结果的质量。
• K-Means聚类算法是比较常用的聚类算法，容易理解和实现相应功能的代码。
• K-Means聚类算法的逻辑为：
  1. 通过计算当前点与每个类别的中心之间的距离，对每个数据点进行分类，然后归到与之距离最近的类别中。
  2. 基于迭代后的结果，计算每一类内全部点的坐标平均值（即质心），作为新类别的中心。
  3. 代重复以上步骤，直到类别的中心点坐标在迭代前后变化不大。

---

植物花卉特征聚类

import torch
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from kmeans_pytorch import kmeans

# 设置运行环境
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")

# 获取数据
plant = pd.read_csv("./plant.csv")
# iris_d = iris[['Sepal_Length', 'Sepal_Width']]
plant_d = plant[['Sepal_Length', 'Sepal_Width', 'Petal_Length', 'Petal_Width']]
plant['target'] = plant['Species']
x = torch.from_numpy(np.array(plant_d))
y = torch.from_numpy(np.array(plant.target))

# 设置聚类数
num_clusters = 3

# 设置聚类模型
"""
X=x 输入数据矩阵，形状通常为 (n_samples, n_features)，代表n_samples个样本，每个样本有n_features个特征
num_clusters 预设的聚类数量（K值），决定数据将被划分为多少类
distance='euclidean'  指定距离度量方式，欧氏距离（默认）表示计算样本与中心点的直线距离
    euclidean：适用于连续型数据，对尺度敏感（需标准化）
    cosine：适合高维稀疏数据（如文本TF-IDF向量）
device=device 指定运行设备（如'cpu'或'cuda:0'），用于控制是否启用GPU加速
"""
cluster_ids_x, cluster_centers = kmeans(
    X=x, num_clusters=num_clusters, distance='euclidean', device=device
)

# 输出聚类ID和聚类中心点
print(cluster_ids_x)
print(cluster_centers)

# 绘制散点图
plt.figure(figsize=(9, 6), dpi=320)

# 不同类别的颜色映射 'cool'：蓝-青渐变色谱 num_clusters：生成与聚类数匹配的颜色数量（确保每类颜色唯一）
cmap = plt.get_cmap('cool', num_clusters)

# 为每个类别单独绘制散点
for i in range(num_clusters):
    plt.scatter(
        x[cluster_ids_x == i, 0], # 当前簇的第一特征值
        x[cluster_ids_x == i, 1], # 当前簇的第二特征值
        c=[cmap(i)],              # 使用颜色映射
        label=f'Cluster {i+1}',   # 图例标签（从1开始计数）
        marker="D"                # 菱形标记（提升可区分性）
    )

# 聚类中心标记
plt.scatter(
    cluster_centers[:, 0],        # 中心点第一维度坐标
    cluster_centers[:, 1],        # 中心点第二维度坐标
    c='white',                    # 填充色为白
    alpha=0.6,                    # 半透明效果（避免遮挡背景）
    edgecolors='black',           # 黑色边框强化对比
    linewidths=2,                 # 边框粗细
    label='Cluster Centers'       # 图例标签
)

# 添加图题和坐标轴标签
plt.title('K-Means Clustering of Flower Characteristics')
plt.xlabel('Sepal Length')
plt.ylabel('Sepal Width')

# 显示图例
plt.legend()
# 自动调整子图/标签间距
plt.tight_layout()
# 渲染图像
plt.show()

running k-means on cuda..
[running kmeans]: 10it [00:00, 69.02it/s, center_shift=0.000000, iteration=10, tol=0.000100]
tensor([1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
        1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
        1, 1, 2, 0, 2, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
        0, 0, 0, 0, 0, 2, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
        0, 0, 0, 0, 2, 0, 2, 2, 2, 2, 0, 2, 2, 2, 2, 2, 2, 0, 0, 2, 2, 2, 2, 0,
        2, 0, 2, 0, 2, 2, 0, 0, 2, 2, 2, 2, 2, 0, 2, 2, 2, 2, 0, 2, 2, 2, 0, 2,
        2, 2, 0, 2, 2, 0])
tensor([[5.8836, 2.7410, 4.3885, 1.4344],
        [5.0060, 3.4280, 1.4620, 0.2460],
        [6.8538, 3.0769, 5.7154, 2.0538]])

主成分分析（PCA）

• 主成分分析（Principal Component Analysis，PCA）是一个线性变换，它把数据变换到一个新的坐标系统中，使得任何数据投影的第一大方差在第一主成分上，第二大方差在第二主成分上，以此类推。

主成分分析简介

• 在研究多变量问题时，变量过多会增加计算和分析的复杂性。我们希望在定量分析中使用较少变量并获得更多信息。主成分分析正是为此而生，是解决这一问题的理想工具。
• 主成分分析常用于降低数据集的维度，目标是保留对数据方差贡献最大的特征。通过保留低阶主成分并忽略高阶主成分，这些低阶成分通常能反映数据中最重要的方面。例如，在评估科普书籍的开发和利用时，涉及多项指标，如科普创作人数、科普作品发行量和科普产业化等。经过主成分分析，确定几个主成分作为综合评价的指标，减少变量数量，同时保持一定的可信度，从而更容易评估科普效果。

成分分析建模

• 主成分分析（PCA）是一种多元统计分析方法，旨在通过线性变换将多个相关变量转化为较少的重要变量。其基本思想是将原本具有一定相关性的多个变量组合成一组新的互相独立的综合指标，从而替代原有指标。

• 具体而言，主成分分析通过正交变换将相关的随机向量转换为不相关的新随机向量。这一过程在代数上表现为将原随机向量的协方差矩阵转变为对角形矩阵，而在几何上则是将原始坐标系转换为新的正交坐标系，使得这些新坐标轴指向样本点分布最广的几个方向。

• 通过这种变换，几个方差较大的新变量（主成分）能够综合反映原始多个变量所包含的主要信息，同时每个主成分也具有自身特定的意义。这种降维处理不仅减少了变量的数量，也有助于提高数据分析的效率和可解释性，使得后续的数据分析和挖掘变得更加简单和清晰。
  $$\begin{array}{l}{z}_1=u_{11}{X}_1+u_{12}{X}_2+\cdots +u_{1p}{X}_p\\ \\ z_2=u_{21}{X}_1+u_{22}{X}_2+\cdots +u_{2p}{X}_p\\ \\ \dots \\ z_p=u_{p1}{X}_1+u_{p2}{X}_2+\cdots +u_{pp}{X}_p\end{array}$$

• $z_1,z_2,\dots ,z_p$为$p$个主成分

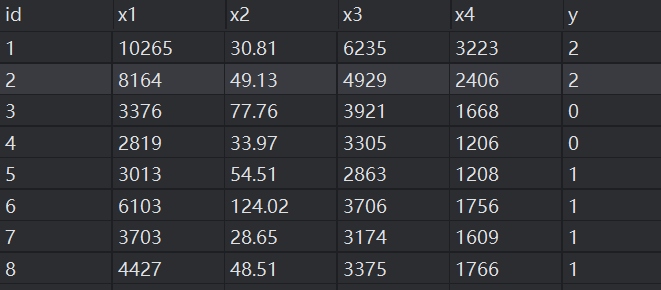
地区竞争力指标降维

• 数据表中选取6个指标，分别是人均GDP，固定资产投资，社会消费品销售总额，农村人均收入等，利用分析因子分析提取公共因子，分析衡量发展因素的指标。
  

import torch
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
from torch.autograd import Variable

# 读取数据 并复制
region = pd.read_csv('./region.csv')
region_data=region[['x1','x2','x3','x4']]
region['target']=region['y']

# 变量特征降维
# 创建一个主成分分析模型，并设置降维后的特征数为2
pca_model = PCA(n_components=2)
#  使用拟合和转换方法对数据进行主成分分析
region_data=pca_model.fit_transform(region_data)

# 转化为NumPy数组
x=torch.from_numpy(region_data)
y=torch.from_numpy(np.array(region['target']))
# 将x和y转化为Variable对象
x,y=Variable(x),Variable(y)
# 解决 mat1 and mat2 must have the same dtype, but got Double and Float
x = x.float()
# 设置网络结构 输入2个特征，输出3个分类
net =torch.nn.Sequential(
    torch.nn.Linear(2, 10),
    torch.nn.ReLU(),
    torch.nn.Linear(10, 3),
)

# 设置优化器和随机梯度下降
optimizer = torch.optim.SGD(net.parameters(), lr=0.00001) # 随机梯度下降 学习率设置为0.00001
loss_func = torch.nn.CrossEntropyLoss() # 损失函数为交叉熵损失函数

# 训练模型
# 存储训练过程中的指标
accuracies = []
losses = []
epochs=1000
# 创建画布（假设每 100 步绘制一次，共 10 张子图）
fig, axes = plt.subplots(5, 2, figsize=(10, 20))
axes = axes.flatten()

for t in range(epochs):
    out = net(x)
    loss = loss_func(out, y)
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()

    # 每 100 次记录一次准确率和损失
    if t % 100 == 0 :
        prediction = torch.max(out, 1)[1]
        pred_y = prediction.data.numpy()
        target_y = y.data.numpy()

        accuracy = float((pred_y == target_y).astype(int).sum()) / float(target_y.size)
        current_loss = loss.item()

        accuracies.append(accuracy)
        losses.append(current_loss)

        idx = t // 100  # 记录第几个子图
        ax = axes[idx]

        # 绘制散点图
        sc = ax.scatter(region_data[:, 0], region_data[:, 1], c=pred_y, s=50, cmap='rainbow')
        ax.set_title(f"Iteration {t}\nAcc: {accuracy:.2%}, Loss: {current_loss:.4f}")

        # 添加 x 和 y 轴标签
        ax.set_xlabel("PCA Feature 1", fontsize=8)
        ax.set_ylabel("PCA Feature 2", fontsize=8)
        ax.tick_params(axis='both', which='major', labelsize=6)  # 减小刻度字体大小以适应布局

plt.tight_layout()
plt.show()
# 保存网络模型（结构+参数）
torch.save(net, './net.pkl')
# 保存网络的状态字典 （参数）
torch.save(net.state_dict(), './net_params.pkl')