经典面试题（三）附答案算法+数据结构+代码微软Microsoft、谷歌Google、百度、腾讯

最新推荐文章于 2022-04-15 19:28:06 发布

yangxi_001

最新推荐文章于 2022-04-15 19:28:06 发布

阅读量788

点赞数

分类专栏：算法笔试面试

算法同时被 2 个专栏收录

22 篇文章 1 订阅

订阅专栏

笔试面试

16 篇文章 0 订阅

订阅专栏

1.判断单链表是否有环，要求空间尽量少（2011年MTK）

如何找出环的连接点在哪里？

如何知道环的长度？

很经典的题目。

1.判断是否有环。使用两个指针。一个每次前进1，另一个每次前进2，且都从链表第一个元素开始。显然，如果有环，两个指针必然会相遇。

2.环的长度。记下第一次的相遇点，这个指针再次从相遇点出发，直到第二次相遇。此时，步长为1的指针所走的步数恰好就是环的长度。

3.环的链接点。记下第一次的相遇点，使一个指针指向这个相遇点，另一个指针指向链表第一个元素。然后，两个指针同步前进，且步长都为1。当两个指针相遇时所指的点就是环的连接点。

链接点这个很不明显，下面解释一下。

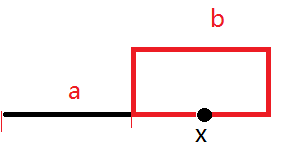
如图，设链表不在环上的结点有a个，在环上的结点有b个，前两个指针第一次在第x个结点相遇。

S( i )表示经过的总步长为i之后，所访问到的结点。

显然，环的链接点位S( a )，即从起点经过a步之后所到达的结点。

现在要证明：

从第一次的相遇点x再经过a步之后可到达链接点S( a ),即 S( x + a ) = S( a )

由环的周期性可知，只要 a = tb 其中( t = 1, 2, …. )，则S( x + a ) = S( a )

如何证明a = tb？

再看看已知条件，当两个指针第一次相遇时，必有S( x ) = S( 2x )

由环的周期性可知，必有 2x = x + bt, 即x = tb.

[cpp]view plaincopy 
   
 struct Node  
 {  
     int data;  
     Node* next;  
   
     Node( int value ): data(value), next(NULL) {};  
 };  
   
 //判断单链表是否有环  
 bool IsCircle( Node *pHead )  
 {  
     //空指针 或 只有一个元素且next为空时，必无环  
     if( pHead == NULL || pHead->next == NULL ) return false;  
       
     Node *pSlow = pHead;  
     Node *pFast = pHead;  
   
     while( ( pFast != NULL ) && ( pFast->next != NULL )  )  
     {  
         //分别按步长1、2前进  
         pSlow = pSlow->next;  
         pFast = pFast->next->next;  
   
         if( pSlow == pFast ) break;  
     }  
     if( ( pFast == NULL ) || ( pFast->next == NULL ) )   
         return false;  
     else   
         return true;  
 }  
   
 //求环的长度  
 int GetLen( Node *pHead )  
 {  
     if( pHead == NULL || pHead->next == NULL ) return false;  
       
     Node *pSlow = pHead;  
     Node *pFast = pHead;  
   
     //求相遇点  
     while( ( pFast != NULL ) && ( pFast->next != NULL )  )  
     {  
         pSlow = pSlow->next;  
         pFast = pFast->next->next;  
   
         if( pSlow == pFast ) break;  
     }  
   
     //计算长度  
     int cnt = 0;  
     while( ( pFast != NULL ) && ( pFast->next != NULL )  )  
     {  
         pSlow = pSlow->next;  
         pFast = pFast->next->next;  
         cnt++;  
   
         //再次相遇时，累计的步数就是环的长度  
         if( pSlow == pFast ) break;  
     }  
     return cnt;  
 }  
 //求环的入口点  
 Node* GetEntrance( Node* pHead )  
 {  
     if( pHead == NULL || pHead->next == NULL ) return false;  
       
     Node *pSlow = pHead;  
     Node *pFast = pHead;  
   
     //求相遇点  
     while( ( pFast != NULL ) && ( pFast->next != NULL )  )  
     {  
         pSlow = pSlow->next;  
         pFast = pFast->next->next;  
   
         if( pSlow == pFast ) break;  
     }  
   
     pSlow = pHead;  
     while( pSlow != pFast )  
     {  
         //同步前进  
         pSlow = pSlow->next;  
         pFast = pFast->next;  
     }  
     return pSlow;  
 }  

2.用非递归的方式合并两个有序链表（2011年MTK）

用递归的方式合并两个有序链表

基本的链表操作，没什么好说的。

非递归：就是把一个链表上的所有结点插入到另一个链表中。

递归：？？

[cpp]view plaincopy 
   
 //两个有序链表的合并  
 Node* merge( Node* pHeadA, Node* pHeadB )  
 {  
     //处理空指针  
     if( pHeadA == NULL || pHeadB == NULL )  
     {  
         return ( pHeadA == NULL ) ? pHeadB : pHeadA;  
     }  
   
     //处理第一个节点  
     Node *px, *py;  
     if( pHeadA->data <= pHeadB->data )  
     {  
         px = pHeadA;    py = pHeadB;  
     }  
     else  
     {  
         px = pHeadB;    py = pHeadA;  
     }  
     Node *pResult = px;  
   
     //将py上的节点按顺序插入到px  
     Node *pre = px;  
     px = px->next;  
     while( py != NULL && px != NULL )  
     {  
         //在px上找到py应该插入的位置  
         while( py != NULL && px != NULL && py->data > px->data )  
         {  
             py = py->next;  
             px = px->next;  
             pre = pre->next;   
         }  
         //py插入到pre和px之间  
         if( py != NULL && px != NULL )  
         {  
             //py指针前移  
             Node* tmp = py;  
             py = py->next;  
   
             //pre指针前移  
             Node* tmpPre = pre;  
             pre = pre->next;  
   
             //插入  
             tmp->next = px;  
             tmpPre->next = tmp;  
   
             //px指针前移  
             px = px->next;             
         }  
         else  
             break;  
     }  
     if( px == NULL ) pre->next = py;  
   
     return pResult;  
 }  

4编程实现：把十进制数(long型)分别以二进制和十六进制形式输出，不能使用printf系列

用位操作实现。十进制数在计算机里本来就是按二进制存储的，因此通过掩码和移位操作很容易输出二进制形式。这里，要注意的一点：对最高位符号位的处理。符号位应该单独处理，否则结果会出错。十六进制的处理和二进制基本相同，只是每次处理四位。

[cpp]view plaincopy 
   
 void LongFormat( long value )  
 {     
     //处理符号位  
     long mask = 0x1 << ( 8 * sizeof(long) - 1 );  
     if( value & mask ) cout << "1";  
     else cout << "0";  
     //转换为二进制  
     mask = 0x1 << ( 8 * sizeof(long) - 2 );  
     for( int i=1; i<8*sizeof(long); i++ )  
     {  
         if( value & mask ) cout << "1";  
         else cout << "0";  
         mask >>= 1;  
     }  
     cout << endl;  
   
     //处理符号位  
     cout << "0x";   
     mask = 0xF << ( 8 * sizeof(long) - 4 );  
     long tmp = ( value & mask ) >> ( 8 * sizeof(long) - 4 );  
     if( tmp < 10 )  
         cout << tmp;  
     else  
         cout << (char)( 'a' + ( tmp - 10 ) );  
     //转换为十六进制  
     mask = 0xF << ( 8 * sizeof(long) - 8 );  
     for( int i=1; i<2*sizeof(long); i++ )  
     {  
         tmp = ( value & mask ) >> ( 8 * sizeof(long) - 4 * i - 4 );  
         if( tmp < 10 )  
             cout << tmp;  
         else  
             cout << (char)( 'a' + ( tmp - 10 ) );  
   
         mask >>= 4;   
     }  
 }  

5.编程实现：找出两个字符串中最大公共子字符串,如"abccade","dgcadde"的最大子串为"cad"

有人说：可用KMP。可惜KMP忘了，找时间补一下。

还有人说：用两个字符串，一个作行、一个作列，形成一个矩阵。相同的位置填1，不同的位置填0。然后找哪个斜线方向上1最多，就可以得到最大公共子字符串。空间复制度0( m*n )，感觉时间上也差不多O( m*n )

没想到什么好办法，只会用最笨的办法O( m*n )。即，对于字符串A中的每个字符，在字符串B中找以它为首的最大子串。哎，即便是这个最笨的方法，也写了好长时间，汗。

[cpp]view plaincopy 
   
 void GetSubStr( char *strA, char *strB, char *ans )  
 {     
     int max = 0;  
     char *pAns = NULL;  
   
     //遍历字符串A  
     for( int i=0; *(strA+i) != '\0'; i++ )  
     {  
         //保存strB的首地址，每次都从strB的第一个元素开始比较  
         char *pb = strB;  
         while( *pb != '\0' )  
         {  
             //保存strA的首地址  
             char *pa = strA + i;  
             int cnt = 0;  
             char *pBegin = pb;  
   
             //如果找到一个相等的元素  
             if( *pb == *pa )  
             {  
                 while( *pb == *pa && *pb != '\0' )   
                 {  
                     pa++;  
                     pb++;  
                     cnt++;  
                 }  
                 if( cnt > max )  
                 {  
                     max = cnt;  
                     pAns = pBegin;  
                 }     
                 if( *pb == '\0' ) break;  
             }  
             else  
                 pb++;             
         }         
     }  
     //返回结果  
     memcpy( ans, pAns, max );     
     *(ans+max) = '\0';  
 }  

6.有双向循环链表结点定义为：

struct node

{

int data;

struct node *front,*next;

};

有两个双向循环链表A，B，知道其头指针为：pHeadA,pHeadB，请写一函数将两链表中data值相同的结点删除。

没什么NB算法。就是遍历对链表A，对A的每个元素，看它是否在链表B中出现。如果在B中出现，则把所有的出现全部删除，同时也在A中删除这个元素。

思路很简单，实现起来也挺麻烦。毕竟，双向循环链表也算是线性数据结构中最复杂的了。如何判断双向循环链表的最后一个元素？p->next == pHead.

删除操作：

双向循环链表只有一个节点时

双向循环链表至少有两个节点时

[cpp]view plaincopy 
   
 struct Node  
 {   
   int data;  
   struct Node *front,*next;  
   Node( int value ): data( value ), front( NULL ), next( NULL ) { };  
   void SetPointer( Node *pPre, Node *pNext ) { front = pPre; next = pNext; };  
 };  
   
 //如果成功删除返回真。否则，返回假。  
 bool DeleteValue( Node *&pHead, int target )  
 {  
     if( pHead == NULL ) return false;     
   
     //至少有两个元素  
     bool flag = false;  
     Node* ph = pHead;  
     while( ph->next != pHead  )  
     {  
         Node *pPre = ph->front;  
         Node *pNext = ph->next;  
   
         if( ph->data == target )  
         {  
             //如果删除的是第一个元素  
             if( ph == pHead ) pHead = ph->next;            
   
             pPre->next = pNext;  
             pNext->front = pPre;   
   
             Node *tmp = ph;  
             delete tmp;  
               
             //设置删除标记  
             flag = true;  
         }  
         ph = pNext;  
     }  
     //只有一个元素或最后一个元素  
     if( ph->next == pHead )  
     {  
         if( ph->data == target )  
         {  
             //如果要删除的是最后一个元素  
             if( ph->front != ph )  
             {                 
                 Node *pPre = ph->front;  
                 Node *pNext = ph->next;  
                 pPre->next = pNext;  
                 pNext->front = pPre;   
   
                 Node *tmp = ph;  
                 delete tmp;  
             }  
             else  
             {  
                 delete pHead;  
                 pHead = NULL;             
             }  
             flag = true;              
         }         
     }  
     return flag;  
 }  
   
   
 void DeleteSame( Node *&pHeadA, Node *&pHeadB )  
 {  
     if( pHeadA != NULL && pHeadB != NULL )  
     {  
         Node *pa = pHeadA;  
         while( pa->next != pHeadA )  
         {             
             //如果B中含有pa->data，并且已经删除            
             if( DeleteValue( pHeadB, pa->data ) )  
             {  
                 //在A中删除pa->data  
                 Node *tmp = pa->next;  
                 DeleteValue( pHeadA, pa->data );  
                 pa = tmp;  
             }  
             else  
                 pa = pa->next;  
         }  
         //只有一个元素或最后一个元素               
         if( DeleteValue( pHeadB, pa->data ) )  
         {  
             DeleteValue( pHeadA, pa->data );  
         }         
     }  
 }  

7.设计函数int atoi(char *s)。

int i=(j=4,k=8,l=16,m=32); printf(“%d”, i); 输出是多少？

解释局部变量、全局变量和静态变量的含义。

解释堆和栈的区别。

论述含参数的宏与函数的优缺点。

1.字符串转整形，嘿嘿，前面已写过了。

2.逗号表达式的值等于最后一个逗号之后的表达式的值。对应本题，即i=(m=32)

3.局部变量：在函数内定义的变量。作用域范围：只在定义它的块内有效。

全局变量：在函数之外定义的变量。作用域范围：从定义的地方开始直到文件末尾都有效。

静态变量：static变量，属于静态存储方式。静态局部变量在函数内定义，生存期是整个源代码。但是，作用域范围只在定义它的函数内有效。静态全局变量与一般的全局变量：一般全局变量在整个源程序内有效，静态全局变量只在所在文件内有效。

4.堆：一般new出来的变量都在堆里，这里变量要由程序员自己管理，即在不用的时候要及时释放，防止内存泄露。

栈：一般局部变量、函数的参数都在栈里，他们是由编译器来自动管理的。

8.顺时针打印矩阵

题目：输入一个矩阵，按照从外向里以顺时针的顺序依次打印出每一个数字。

例如：如果输入如下矩阵：

1 2 3 4

5 6 7 8

9 10 11 12

13 14 15 16

则依次打印出数字, 2, 3, 4, 8, 12, 16, 15, 14, 13, 9, 5, 6, 7, 11, 10。

分析：包括Autodesk、EMC在内的多家公司在面试或者笔试里采用过这道题

本来想写递归的，结果递归的终止条件比较复杂。因为每次把最外面一圈都出来了，所以矩形的行列都减小2，而且还要记录当前矩形的起始位置。递归终止条件，要考虑行列为0、1的情况。哎，想不清楚。最后还是非递归的好写。也很简单，没啥所的，直接看代码把。

[cpp]view plaincopy 
   
 const int MAX_ROW = 100;  
 const int MAX_COL = 100;  
   
 void PrintMatrix( int data[][MAX_COL], int row, int col )  
 {  
     int top = 0;  
     int bottom = row-1;  
     int left = 0;  
     int right = col-1;  
   
     int cnt = 0;  
     int total = row * col;  
     while( cnt < total )  
     {  
         //从左到右，打印最上面一行  
         int j;  
         for( j=left; j<=right && cnt<total; j++ )  
         {  
             cout << data[top][j] <<" ";  
             cnt++;  
         }  
         top++;  
   
         //从上到下，打印最右面一列  
         for( j=top; j<=bottom && cnt<total; j++ )  
         {  
             cout << data[j][right] << " ";  
             cnt++;  
         }  
         right--;  
   
         //从右到左，打印最下面一行  
         for( j=right; j>=left && cnt<total; j-- )  
         {  
             cout << data[bottom][j] << " ";  
             cnt++;  
         }  
         bottom--;  
   
         //从下到上，打印最左边一列  
         for( j=bottom; j>=top && cnt<total; j-- )  
         {  
             cout << data[j][left] << " ";  
             cnt++;  
         }  
         left++;  
     }             
 }  

9.对称子字符串的最大长度

题目：输入一个字符串，输出该字符串中对称的子字符串的最大长度。

比如输入字符串“google”，由于该字符串里最长的对称子字符串是“goog”，因此输出。

分析：可能很多人都写过判断一个字符串是不是对称的函数，这个题目可以看成是该函数的加强版

10.用1、2、3、4、5、6这六个数字，写一个main函数，打印出所有不同的排列，如：512234、412345等，要求："4"不能在第三位，"3"与"5"不能相连.

先不考虑限制条件，我们可以用递归打印出所有的排列（嘿嘿，这个前面写过，可以用递归处理）。然后，只要在递归终止时，把限制条件加上，这样只把满足条件的排列打印出来，就可以了。

[cpp]view plaincopy 
   
 bool IsValid( char *str )  
 {  
     for( int i=1; *(str+i) != '\0'; i++ )  
     {  
         if( i == 2 && *(str+i) == '4' ) return false;  
   
         if( *(str+i) == '3' && *(str+i-1) == '5' || *(str+i) == '5' && *(str+i-1) == '3' )  
             return false;  
     }  
     return true;  
 }  
   
 void PrintStr( char *str, char *start )  
 {  
     if( str == NULL ) return;  
       
     if( *start == '\0' )  
     {  
         if( IsValid( str ) ) cout << str << endl;  
     }  
   
     for( char *ptmp = start; *ptmp != '\0'; ptmp++ )  
     {  
         char tmp = *start;  
         *start = *ptmp;  
         *ptmp = tmp;  
   
         PrintStr( str, start+1 );  
   
         tmp = *start;  
         *start = *ptmp;  
         *ptmp = tmp;   
     }  
 }  

11。微软面试题

一个有序数列，序列中的每一个值都能够被2或者3或者5所整除，1是这个序列的第一个元素。求第1500个值是多少？

2、3、5的最小公倍数是30。[ 1, 30]内符合条件的数有22个。如果能看出[ 31, 60]内也有22个符合条件的数，那问题就容易解决了。也就是说，这些数具有周期性，且周期为30.

第1500个数是：1500/22=68 1500%68=4。也就是说：第1500个数相当于经过了68个周期，然后再取下一个周期内的第4个数。一个周期内的前4个数：2,3,4,5。

故，结果为68*30=2040+5=2045

12.从尾到头输出链表

题目：输入一个链表的头结点，从尾到头反过来输出每个结点的值。链表结点定义如下：

struct ListNode

{

int m_nKey;

ListNode* m_pNext;

};

分析：这是一道很有意思的面试题。该题以及它的变体经常出现在各大公司的面试、笔试题中。

链表的反向输出。前面我们讨论过：链表的逆序，使用3个额外指针，遍历一遍链表即可完成。这里当然可以先把链表逆序，然后再输出。链表上使用递归一般也很简单，虽然递归要压栈，但程序看起来很简洁。

[cpp]view plaincopy 
   
 struct ListNode  
 {  
     int  m_nKey;  
     ListNode* m_pNext;  
 };  
   
 void PrintReverse( ListNode* pHead )  
 {  
     ListNode* ph = pHead;  
     if( ph != NULL )  
     {  
         PrintReverse( ph->m_pNext );  
         cout << ph->m_nKey << " ";  
     }  
 }  