剑指offer面试题：求二叉树的镜像（递归、循环解法及测试用例）

题目：给定二叉树，将其变换为源二叉树的镜像。

二叉树的定义如下：

struct TreeNode

{

    int val;

    TreeNode* left;

    TreeNode* right;

};

输入描述:

二叉树的镜像定义：

    源二叉树

         8

        /  \

      6   10

     / \    / \

   5  7  9 11

     镜像二叉树

         8

        /  \

     10    6

     / \     / \

   11 9  7  5

思路：

观察上面两个二叉树，很容易就可以得出下面求一棵树镜像的过程：

 

      先序遍历这棵树的每个结点，如果遍历到的结点有子结点，则交换它的两个子结点。当交换完所有非叶子结点的左右子结点之后，就得到了树的镜像。

      图制作的有点丑，但是基本可以表达清楚原理了，咳咳，若喷，请轻喷。

 方法一：递归遍历法：

//递归实现二叉树的镜像，按照先序遍历，如果遇到空的节点或者叶子节点就返回，否则交换两个子树后再改变左右子树  
void MirrorBinaryTree1(BinaryTreeNode* root)
{
	if (root == NULL || (root->leftchild == NULL && root->rightchild == NULL))
	{
		return;
	}

	BinaryTreeNode * tmp = root->leftchild;
	root->leftchild = root->rightchild;
	root->rightchild = tmp;

	if (root->leftchild)
	{
		MirrorBinaryTree1(root->leftchild);
	}
	if (root->rightchild)
	{
		MirrorBinaryTree1(root->rightchild);
	}
	
}

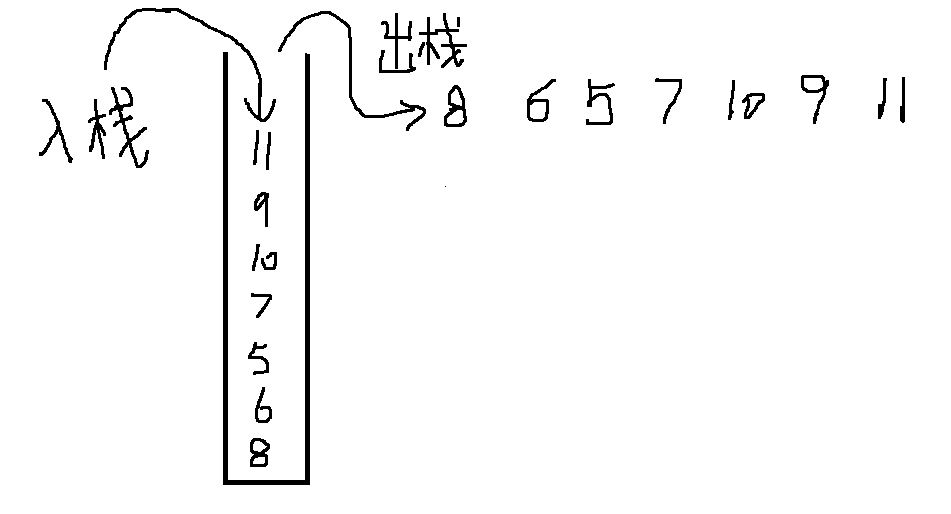
方法二：循环压栈实现二叉树镜像

循环压栈示意图：

//循环实现二叉树的镜像，利用栈的“后进先出”特性打印
void MirrorBinaryTree2(BinaryTreeNode* root)
{
	if (root == NULL)
	{
		return;
	}

	stack<BinaryTreeNode*> stackTreeNode;
	stackTreeNode.push(root);

	while (stackTreeNode.size() > 0)
	{
		BinaryTreeNode *parent = stackTreeNode.top();
		stackTreeNode.pop();

		BinaryTreeNode *Temp = parent->leftchild;
		parent->leftchild = parent->rightchild;
		parent->rightchild = Temp;

		if (parent->leftchild)
		{
			stackTreeNode.push(parent->leftchild);
		}

		if (parent->rightchild)
		{
			stackTreeNode.push(parent->rightchild);
		}

	}
}

 进行功能测试的时候分五种情况：

（1）测试完全二叉树：除了叶子节点，其他节点都有两个子节点

         8

        /  \

      6   10

     / \    / \

   5  7  9 11

（2） 测试二叉树：出叶子结点之外，左右的结点都有且只有一个左子结点
            8

           /
          7   

         /
        6 

       /
      5

     /
    4

（3） 测试二叉树：出叶子结点之外，左右的结点都有且只有一个右子结点
       
            8

             \
             7   

               \
               6 

                \
                 5

                  \
                  4

（4） 测试空二叉树：根结点为空指针

（5） 测试只有一个结点的二叉树

                           

完整代码及五种测试用例：

#include<iostream>    
#include<stack>  
using namespace std;

struct BinaryTreeNode
{
	int data;
	BinaryTreeNode* leftchild;
	BinaryTreeNode* rightchild;

	BinaryTreeNode(int t)
	{
		data = t;
		leftchild =  NULL;
		rightchild = NULL;
	}
};


void PreorderTravel(BinaryTreeNode* root)
{
	if (root == NULL)
	{
		return;
	}
	cout <<root->data << "    ";
	PreorderTravel(root->leftchild);
	PreorderTravel(root->rightchild);
}

//递归实现二叉树的镜像，按照先序遍历，如果遇到空的节点或者叶子节点就返回，否则交换两个子树后再改变左右子树  
void MirrorBinaryTree1(BinaryTreeNode* root)
{
	if (root == NULL || (root->leftchild == NULL && root->rightchild == NULL))
	{
		return;
	}

	BinaryTreeNode * tmp = root->leftchild;
	root->leftchild = root->rightchild;
	root->rightchild = tmp;

	if (root->leftchild)
	{
		MirrorBinaryTree1(root->leftchild);
	}
	if (root->rightchild)
	{
		MirrorBinaryTree1(root->rightchild);
	}
	
}

//循环实现二叉树的镜像，利用栈的“后进先出”特性打印
void MirrorBinaryTree2(BinaryTreeNode* root)
{
	if (root == NULL)
	{
		return;
	}

	stack<BinaryTreeNode*> stackTreeNode;
	stackTreeNode.push(root);

	while (stackTreeNode.size() > 0)
	{
		BinaryTreeNode *parent = stackTreeNode.top();
		stackTreeNode.pop();

		BinaryTreeNode *Temp = parent->leftchild;
		parent->leftchild = parent->rightchild;
		parent->rightchild = Temp;

		if (parent->leftchild)
		{
			stackTreeNode.push(parent->leftchild);
		}

		if (parent->rightchild)
		{
			stackTreeNode.push(parent->rightchild);
		}

	}
}


// ====================测试代码====================


// 测试完全二叉树：除了叶子节点，其他节点都有两个子节点
//            8
//      6        10
//   5  7      9  11

BinaryTreeNode* root;
void Test1()
{
	root = new BinaryTreeNode(8);
	root->leftchild = new BinaryTreeNode(6);
	root->rightchild = new BinaryTreeNode(10);
	BinaryTreeNode* tmp = root->leftchild;
	tmp->leftchild = new BinaryTreeNode(5);
	tmp->rightchild = new BinaryTreeNode(7);
	tmp = root->rightchild;
	tmp->leftchild = new BinaryTreeNode(9);
	tmp->rightchild = new BinaryTreeNode(11);

	cout << "Test1:测试完全二叉树,除了叶子节点，其他节点都有两个子节点" << endl;
	cout << "原二叉树的先序遍历" << endl;
	PreorderTravel(root);
	cout << endl;
	
	MirrorBinaryTree1(root);
	cout << "二叉树镜像后的先序遍历" << endl;
	PreorderTravel(root);
	cout << endl;

	/*MirrorBinaryTree2(root);
	cout << "二叉树镜像后的先序遍历" << endl;
	PreorderTravel(root);
	cout << endl;*/
}


// 测试二叉树：出叶子结点之外，左右的结点都有且只有一个左子结点
//            8
//          7   
//        6 
//      5
//    4
void Test2()
{
	root = new BinaryTreeNode(8);
	root->leftchild = new BinaryTreeNode(7);
	root->rightchild = NULL;

	BinaryTreeNode* tmp = root->leftchild;
	tmp->leftchild = new BinaryTreeNode(6);
	tmp->rightchild = NULL;

	tmp = tmp->leftchild;
	tmp->leftchild = new BinaryTreeNode(5);
	tmp->rightchild = NULL;

	tmp = tmp->leftchild;
	tmp->leftchild = new BinaryTreeNode(4);
	tmp->rightchild = NULL;

	cout << "Test2: 测试二叉树,出叶子结点之外，左右的结点都有且只有一个左子结点" << endl;
	cout << "原二叉树的先序遍历" << endl;
	PreorderTravel(root);
	cout << endl;

	MirrorBinaryTree1(root);
	cout << "二叉树镜像后的先序遍历" << endl;
	PreorderTravel(root);
	cout << endl;

	/*MirrorBinaryTree2(root);
	cout << "二叉树镜像后的先序遍历" << endl;
	PreorderTravel(root);
	cout << endl;*/
}

// 测试二叉树：出叶子结点之外，左右的结点都有且只有一个右子结点
//            8
//             7   
//              6 
//               5
//                4
void Test3()
{
	root = new BinaryTreeNode(8);
	root->leftchild = NULL;
	root->rightchild = new BinaryTreeNode(7);

	BinaryTreeNode* tmp = root->rightchild;
	tmp->leftchild = NULL;
	tmp->rightchild = new BinaryTreeNode(6);
	
	tmp = tmp->rightchild;
	tmp->leftchild = NULL;
	tmp->rightchild = new BinaryTreeNode(5);
	
	tmp = tmp->rightchild;
	tmp->leftchild = NULL;
	tmp->rightchild = new BinaryTreeNode(4);

	cout << "Test3:测试二叉树出叶子结点之外，左右的结点都有且只有一个右子结点" << endl;
	cout << "原二叉树的先序遍历" << endl;
	PreorderTravel(root);
	cout << endl;

	MirrorBinaryTree1(root);
	cout << "二叉树镜像后的先序遍历" << endl;
	PreorderTravel(root);
	cout << endl;

	/*MirrorBinaryTree2(root);
	cout << "二叉树镜像后的先序遍历" << endl;
	PreorderTravel(root);
	cout << endl;*/
}

// 测试空二叉树：根结点为空指针
void Test4()
{
	root = NULL;

	cout << "Test4:测试空二叉树,根结点为空指针" << endl;
	cout << "原二叉树的先序遍历" << endl;
	PreorderTravel(root);
	cout << endl;

	MirrorBinaryTree1(root);
	cout << "二叉树镜像后的先序遍历" << endl;
	PreorderTravel(root);
	cout << endl;

	/*MirrorBinaryTree2(root);
	cout << "二叉树镜像后的先序遍历" << endl;
	PreorderTravel(root);
	cout << endl;*/
}


// 测试只有一个结点的二叉树
void Test5()
{
	root = new BinaryTreeNode(8);
	root->leftchild = NULL;
	root->rightchild = NULL;

	cout << "Test5:测试只有一个结点8的二叉树" << endl;
	cout << "原二叉树的先序遍历" << endl;
	PreorderTravel(root);
	cout << endl;

	MirrorBinaryTree1(root);
	cout << "二叉树镜像后的先序遍历" << endl;
	PreorderTravel(root);
	cout << endl;

	/*MirrorBinaryTree2(root);
	cout << "二叉树镜像后的先序遍历" << endl;
	PreorderTravel(root);
	cout << endl;*/
}


int main()
{
	Test1();
	Test2();
	Test3();
	Test4();
	Test5();

	system("pause");
	return 0;
}

运行结果：

Test1:测试完全二叉树,除了叶子节点，其他节点都有两个子节点

原二叉树的先序遍历

8       6       5       7       10      9       11

二叉树镜像后的先序遍历

8       10      11      9       6       7       5

Test2: 测试二叉树,出叶子结点之外，左右的结点都有且只有一个左子结点

原二叉树的先序遍历

8       7       6       5       4

二叉树镜像后的先序遍历

8       7       6       5       4

Test3:测试二叉树出叶子结点之外，左右的结点都有且只有一个右子结点

原二叉树的先序遍历

8       7       6       5       4

二叉树镜像后的先序遍历

8       7       6       5       4

Test4:测试空二叉树,根结点为空指针

原二叉树的先序遍历

 

二叉树镜像后的先序遍历

 

Test5:测试只有一个结点8的二叉树

原二叉树的先序遍历

8

二叉树镜像后的先序遍历

8

请按任意键继续. . .