作者:寒小阳
时间:2013年9月。
出处:http://blog.csdn.net/han_xiaoyang/article/details/11938973。
声明:版权所有,转载请注明出处,谢谢。
0、前言
当年博主自己参加校招笔试面试时就遇到过几次catalan数相关的题目,今年又到了互联网招聘季,翻看下近期各大公司的笔试面试题,发现它依旧是很容易被考察的点。尴尬的是,博主自己觉得catalan数相关的题目不好归类到某种具体的数据结构或者算法里面(计算catalan数的那个小程序不算算法吧。。。),而是比较偏数学题。
不管怎么说,它是笔试面试中容易出现的东西,而有一部分同学可能不大熟悉。这里把catalan数的由来和笔试面试中涉及它的相关问题整理了一下,单独发一篇文吧,不熟悉的童鞋们看看,可能会有帮助。
一、catalan数由来和性质
1)由来
catalan数(卡塔兰数)取自组合数学中一个常在各种计数问题中出现的数列。以比利时的数学家欧仁·查理·卡塔兰 (1814–1894)命名。
卡塔兰数的一般项公式为
令其为h(n)的话,满足h(n)= h(0)*h(n-1)+h(1)*h(n-2) + ... + h(n-1)h(0) (n>=2)
我们从中取出的Cn就叫做第n个Catalan数,前几个Catalan数是:1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, 35357670, …咋看之下没什么特别的,但是Catalan数却是许多计数问题的最终形式。
2)性质
1、Catalan数的基本公式就是上面列出的式子,但是却有一些变形和具体的性质:
这是根据原来的式子推导出来的,大概过程是这样的:
2、有如下的递推式
3、有
4、
二、Catalan数的程序求解
//函数功能: 计算Catalan数列的第n项
//函数参数: 项数n
//返回值: 第n个Catalan数
long Catalan(int n)
{
if(n <= 1)
return 1;
long *h = new long[n+1]; //保存临时结果
h[0] = h[1] = 1; //h(0)和h(1)
for(int i = 2; i <= n; i++) //依次计算h(2),h(3)...h(n)
{
h[i] = 0;
for(int j = 0; j < i; j++) //根据递归式计算 h(i)= h(0)*h(i-1)+h(1)*h(i-2) + ... + h(i-1)h(0)
h[i] += (h[j] * h[i-1-j]);
}
long result = h[n]; //保存结果
delete [] h; //注意释放空间
return result;
}三、Catalan数的应用场景和笔试面试中出现过的题目
1、括号匹配问题
n对括号有多少种匹配方式?
n对括号相当于有2n个符号,n个左括号、n个右括号,可








 本文详细介绍了Catalan数的概念、性质、递推公式,并列举了在括号匹配、进栈出栈问题、二叉树种类等笔试面试中常见的应用场景。通过分析,展示了Catalan数在解决这些问题中的重要作用,帮助读者理解和运用。
本文详细介绍了Catalan数的概念、性质、递推公式,并列举了在括号匹配、进栈出栈问题、二叉树种类等笔试面试中常见的应用场景。通过分析,展示了Catalan数在解决这些问题中的重要作用,帮助读者理解和运用。
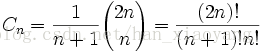
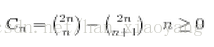
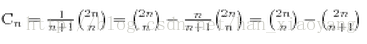

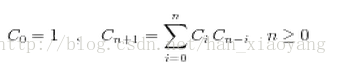
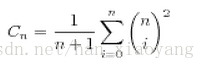
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








