快速排序

上面这边文章我们讲过归并排序的时间复杂度是O(nlogn)，但是需要的空间复杂度是O（N），合并时需要额外的辅助空间，其实还有一种算法，大多数情况下时间复杂度也是O(nlogn)，而且是原地排序算法，不需要偶外的空间协助。快速排序。

其实快速排序也是使用的分治的思想，快速排序的原理比较简单，随机挑选一个元素（一般是挑选第一个），把小于基准元素（选择的元素）的值放置到左边，把大于基准元素的值放置到选择的元素的右边。最后再分别针对左半部分和右半部分进行相同的操作。

比如对于如下的数组，我们选取第一个元素5作为基准元素，则我们如何 不使用额外的空间原地把小于元素5的元素放置于元素5的左边，把大于元素5的元素放置于5的右边？当我们找到元素5的合适位置后。再对基准元素5左边的和基准元素5右边的执行同样的操作即可。

经过上面的分析我们可以写出快速排序算法的算法框架如下。

/**
     * 快速排序入口方法
     *
     * @param nums
     */
    public static void quickSort(int[] nums) {
        quickSort(nums, 0, nums.length - 1);
    }

    private static void quickSort(int[] nums, int p, int r) {
        //递归终止条件
        if (p >= r) return;

        //获取基准位置
        int q = partition(nums, p, r);

        //递归处理基准元素左边的元素
        quickSort(nums, p, q - 1);

        //递归处理基准元素右边的元素
        quickSort(nums, q + 1, r);
    }

    private static int partition(int[] nums, int p, int r) {
        //不使用额外控件，返回基准元素的索引位置，使得基准元素左边的元素都小于基准元素，基准元素右边的都大于基准元素
    }

其实我们可以看出快速排序的大框架非常的简单，重点是partition函数的实现。接下来我们使用图解分析下partiton函数的实现细节，我们还是使用以下数组进行说明。

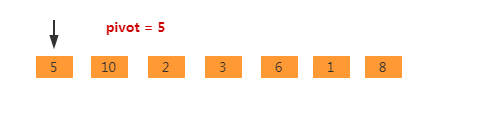
起始时我们可以选取第一个元素作为基准元素。其实此处我们可以使用双指针。

其实partition函数的逻辑就是要为基准元素找到合适的位置。使得基准元素左边的都小于基准元素，右边的都大于基准元素。那也就以为着基准元素目前在的位置是可以被占用的，即我们可以利用这个可以被占用的空间来协助找到基准元素的正确位置。

此处我们使用双指针，left指向第一个位置，right指向最后一个位置，如下图所示。

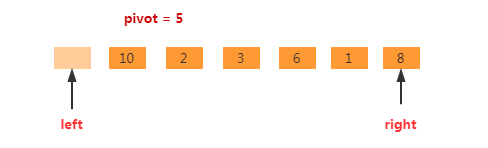
起始时right指针开始移动（此处因为left指针代表可以被占用的位置，所以只能right指针先移动），如果right指针指向的位置比基准元素大，则right指针继续往左移动。如下图

   

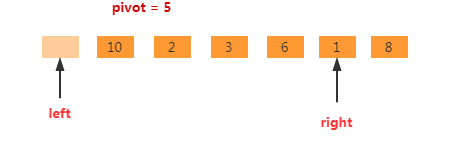
移动到这个位置时right指向的元素（1）比基准元素（5）小了，所以需要把right指向的值赋值到left指向的位置（可以被占用的位置），此处right表示的位置又变为可以被占用的位置。如下图

   

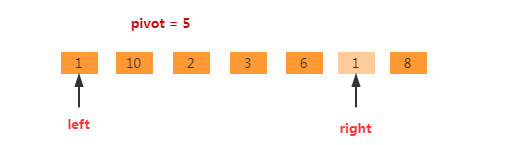
此时因为right表示的位置为可以被占用的位置，所以切换到left来进行判断。执行一样的操作，如果left指向的值（1）比基准元素（5）大，则执行赋值操作，如果比基准元素小，则直接left++即可。如下图

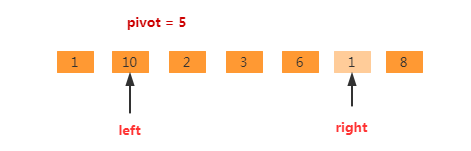
再继续

     

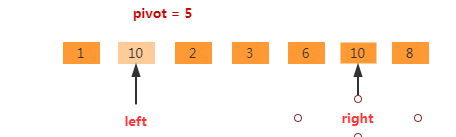
再继续，nums[right]>pivot，执行right--，如下图。

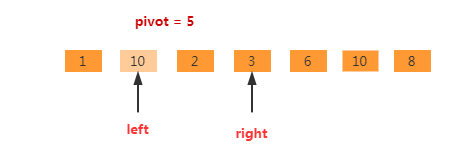
再继续，nums[right] < pivot，执行nums[left]=nums[right]。同时right指向的位置为可以被占用的位置。如下图所示。

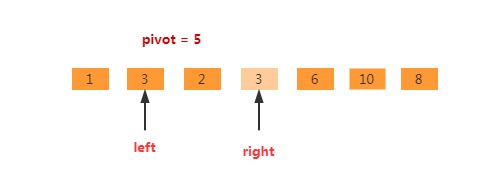
再继续，nums[left]<pivot。则直接执行left++，如下图，此时left == right。不再需要执行操作，left 指向的位置即为基准元素的正确位置

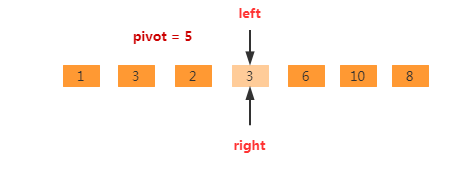
填充基准位置的值，同时返回基准位置的索引。

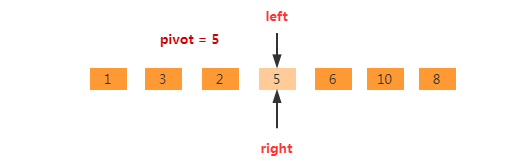
经过上面的分析，即为partition函数的图解过程，代码如下：

private static int partition(int[] nums, int left, int right) {
        //起始时选择左边界作为分隔节点
        int pivot = nums[left];

        //如果left小于right
        while (left < right) {
            //从right开始，如果nums[right]>=pivot。则只需要执行right--即可
            while (left < right && nums[right] >= pivot) {
                right--;
            }
            //如果nums[right] < pivot。则把 right 指向的值设置到left位置。
            nums[left] = nums[right];
            while (left < right && nums[left] <= pivot) {
                left++;
            }
            nums[right] = nums[left];
        }
        nums[left] = pivot;
        return left;
    }

我们来分析一下快速排序的性能。我在讲解快排的实现原理的时候，已经分析了稳定性和空间复杂度。快排是一种原地、不稳定的排序算法。

现在，我们集中精力来看快排的时间复杂度。快排也是用递归来实现的。对于递归代码的时间复杂度，我前面总结的公式，这里也还是适用的。如果每次分区操作，都能正好把数组分成大小接近相等的两个小区间，那快排的时间复杂度递推求解公式跟归并是相同的。所以，快排的时间复杂度也是 O(nlogn)。

但是，公式成立的前提是每次分区操作，我们选择的 pivot 都很合适，正好能将大区间对等地一分为二。但实际上这种情况是很难实现的。

我举一个比较极端的例子。如果数组中的数据原来已经是有序的了，比如 1，3，5，6，8。如果我们每次选择最后一个元素作为 pivot，那每次分区得到的两个区间都是不均等的。我们需要进行大约 n 次分区操作，才能完成快排的整个过程。每次分区我们平均要扫描大约 n/2 个元素，这种情况下，快排的时间复杂度就从 O(nlogn) 退化成了 O(n2)。

为了避免这种一边倒的情况，我们可以使用三数取中法，可以参照这边博文。

https://www.cnblogs.com/ysocean/p/8032632.html