Matlab 基础04 - 冒号Colon operator “：”的使用和复杂应用详析

本文链接：https://blog.csdn.net/yellow_hill/article/details/125122992

本文详细介绍了MATLAB中冒号运算符的使用，包括创建单位间隔和指定间隔的向量，以及在数组索引中的应用，如提取矩阵的行、列和子集。通过实例展示了如何利用冒号进行数据的选取和重组，对于理解MATLAB编程具有指导意义。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

前言：

The colon is one of the most useful operators in MATLAB®. It can create vectors, subscript arrays, and specify for iterations.

冒号在Matlab中主要应用向量和数组下标和for迭代等,在做下标表述的时候，比较晦涩难懂难懂有必要单独讨论一下：

1 表达式：

x = j:k
x = j:i:k
A(:,n)
A(m,:)
A(:)
A(j:k)

1.1 `x = j:k` 【默认间隔1，j为第一维度，k为第二维度】

creates a unit-spaced vector x with elements [j,j+1,j+2,...,j+m] where m = fix(k-j). If j and k are both integers, then this is simply [j,j+1,...,k].

创建一个具备j到j+m的单位间隔向量，每个元素默认增加的步长为1.

【案，默认间隔增加的步长为1，这时候】

【例1】创建一个单位间隔向量：

x = 1:10
x = 1×10

     1     2     3     4     5     6     7     8     9    10


>> y=7:14

y =

     7     8     9    10    11    12    13    14

1.2 x = j:i:k 创建指定间隔的向量

x = j:i:k creates a regularly-spaced vector x using i as the increment between elements. The vector elements are roughly equal to [j,j+i,j+2*i,...,j+m*i] where m = fix((k-j)/i). However, if i is not an integer, then floating point arithmetic plays a role in determining whether colon includes the endpoint k in the vector, since k might not be exactly equal to j+m*i. If you specify nonscalar arrays, then MATLAB interprets j:i:k as j(1):i(1):k(1).

创建一个普通间隔的向量，将i作为元素增加的步长。

【例2】创建一个指定间隔的向量：这个例子里面步长为0.1,这样0开始计算后，正好是有

Create vectors that increment or decrement by a specified value.

Create a vector whose elements increment by 0.1.

>> x = 0:0.1:1

x =

  列 1 至 6

         0    0.1000    0.2000    0.3000    0.4000    0.5000

  列 7 至 11

    0.6000    0.7000    0.8000    0.9000    1.0000

有约束条件：

Output Arguments

collapse all

x — Regularly-spaced vector
row vector

Regularly-spaced vector, returned as a row vector. If j > k, then x = j:k is an empty matrix. More generally, the syntax x = j:i:k returns an empty matrix when:

i, j, or k is an empty input

i == 0

i > 0 and j > k

i < 0 and j < k

1.3 `A(:,n)`, `A(m,:)`, `A(:)`, and `A(j:k)` common indexing expressions 数组的一般标号表达式

A(:,n), A(m,:), A(:), and A(j:k) are common indexing expressions for a matrix A that contain a colon. When you use a colon as a subscript in an indexing expression, such as A(:,n), it acts as shorthand to include all subscripts in a particular array dimension. It is also common to create a vector with a colon for the purposes of indexing, such as A(j:k). Some indexing expressions combine both uses of the colon, as in A(:,j:k).

一般标号表达式，冒号有点像通配符：

先生成一个3by3的矩阵，

A = magic(3)
A = 3×3

     8     1     6
     3     5     7
     4     9     2

A(:,n) is the nth column of matrix A.【第n列所有元素】
A(1,:)
ans = 1×3

     8     1     6
>> A(2,:)

ans =

     3     5     7
A(m,:) is the mth row of matrix A.-【第m行的所有元素】
>> A(:,1)

ans =

     8
     3
     4
>> A(:,2)

ans =

     1
     5
     9
A(:,:,p) is the pth page of three-dimensional array A.【一个page的数据】
>>  B = randn(4,3,2)

B(:,:,1) =

   -0.1924   -1.4224    1.4193
    0.8886    0.4882    0.2916
   -0.7648   -0.1774    0.1978
   -1.4023   -0.1961    1.5877
A(:) reshapes all elements of A into a single column vector. This has no effect if A is already a column vector.【把二维数组的列合并成1列，降维了】
>> A(:)

ans =

     8
     3
     4
     1
     5
     9
     6
     7
     2
注意，3维数组这个操做不行。

A(:,:) reshapes all elements of A into a two-dimensional matrix. This has no effect if A is already a matrix or vector. 【把刚才的一维的又搞成2维的了】
>> A(:,:)

ans =

     8     1     6
     3     5     7
     4     9     2
A(j:k) uses the vector j:k to index into A and is therefore equivalent to the vector [A(j), A(j+1), ..., A(k)].

按照从左到右，从上到下的顺序，将A从元素j到元素k,提取出来，并合成一个向量。
>> A(2:3)

ans =

     3     4
>> A(1:3)

ans =

     8     3     4

A(:,j:k) includes all subscripts in the first dimension but uses the vector j:k to index in the second dimension. This returns a matrix with columns [A(:,j), A(:,j+1), ..., A(:,k)].

这个就组合的意思：这里坐标的参数是向量的第一维度，右边的参数是向量的第二维度：

于是如果A=
>> A(:,:)

ans =

     8     1     6
     3     5     7
     4     9     2
那么， 1到2列的选择为
>> A(:,1:2)

ans =

     8     1
     3     5
     4     9
1到3列的选择为：
>> A(:,1:3)

ans =

     8     1     6
     3     5     7
     4     9     2

3 实例举例和分析：

构建一个4阶的幻方备用：

>> A = magic(4)

A =

    16     2     3    13
     5    11    10     8
     9     7     6    12
     4    14    15     1

再构造一个8阶的幻方备用：

>> B = magic(8)

B =

    64     2     3    61    60     6     7    57
     9    55    54    12    13    51    50    16
    17    47    46    20    21    43    42    24
    40    26    27    37    36    30    31    33
    32    34    35    29    28    38    39    25
    41    23    22    44    45    19    18    48
    49    15    14    52    53    11    10    56
     8    58    59     5     4    62    63     1

3.1 从某个指定行按照指定的顺序摘取数据：

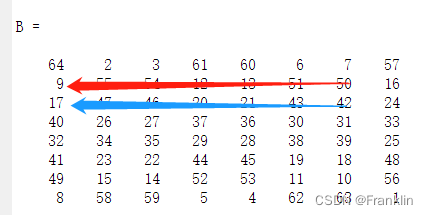
【例1】从幻方B，的第2,3行，从第7列到第1列，倒序或者说减序（-1）摘取数据

>> B(2:3,7:-1:1)

ans =

    50    51    13    12    54    55     9
    42    43    21    20    46    47    17

【案，表征如下】

【例二】幻方A，从第3到4行，2到4列，正序摘取数据，默认为1,所以，可以不写，

>> A(3:4,2:4)

ans =

     7     6    12
    14    15     1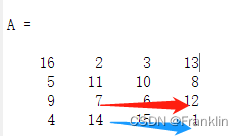

【例3】引用最后一列元素

>> A(:,end)

ans =

    13
     8
    12
     1

【例四】引用第3行，导数第2个数据

>> B(3,end - 1)

ans =

    42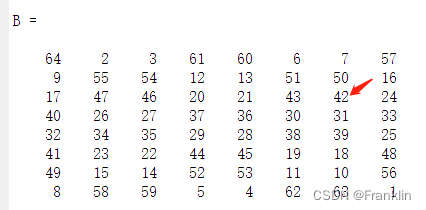

3.2 复杂的数据重组：

继续使用，上一小结生成的幻方矩阵做例子：

例五，摘取不确定的行和列，可以重复，并把他们重新组织起来。

本例，将B的第1,3行的，第2,3列组织起来，注意，第3行，和第2列，第3列都取了2次

>> B([1 3 3],[2 2 3 3])

ans =

     2     2     3     3
    47    47    46    46
    47    47    46    46

3.3 冒号的通配符例子：

例6，我们用：做通配符，将一个3x3的矩阵拓展为 3x3x3x2的四维度的矩阵

>>  C(:,:,1,2)=[1 2 3;4 5 6;7 8 9]

C(:,:,1,1) =

     0     0     0
     0     0     0
     0     0     0


C(:,:,1,2) =

     1     2     3
     4     5     6
     7     8     9

【案，通配符这里占据了第1,2向量维度，我们只给出了一个3x3的矩阵，其他的矩阵自动赋值为0，这里我们定义了维度3by1&维度4by2的一个值，系统自动将3by1的赋值为0】

>> C(:,:,2,2)=[9 8 1;6 5 4;3 2 1]

C(:,:,1,1) =

     0     0     0
     0     0     0
     0     0     0


C(:,:,2,1) =

     0     0     0
     0     0     0
     0     0     0


C(:,:,1,2) =

     1     2     3
     4     5     6
     7     8     9


C(:,:,2,2) =

     9     8     1
     6     5     4
     3     2     1

【案，我们继续赋值维度3by2&维度4by2的值，系统自动赋值其他】

>> C(:,:,3,2)=[5 5 5;5 5 5;5 5 5]

C(:,:,1,1) =

     0     0     0
     0     0     0
     0     0     0


C(:,:,2,1) =

     0     0     0
     0     0     0
     0     0     0


C(:,:,3,1) =

     0     0     0
     0     0     0
     0     0     0


C(:,:,1,2) =

     1     2     3
     4     5     6
     7     8     9


C(:,:,2,2) =

     9     8     1
     6     5     4
     3     2     1


C(:,:,3,2) =

     5     5     5
     5     5     5
     5     5     5

【同理，构造了整个矩阵】