线性代数_第二章矩阵

1.矩阵

只有一行（列）的矩阵：行（列）矩阵，行（列）向量。

1.1 线性变换：

• 系数矩阵：系数为矩阵：
  
• 单位矩阵
  主对角线上的元素是1，其余元素为0；线性变换为n个恒等式
  
• 对角矩阵：

主对角线上的元素是等式系数，其余元素为0；线性变换为n个线性方程

1.2 投影变换

向量在x轴，y轴上的投影，

1.3 旋转变换

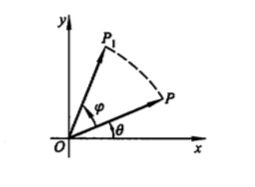
2.矩阵的运算

2.1 矩阵与矩阵相乘

note：

线性变换：

2.2 矩阵的转置

• 定义：

• 运算规律：

• 对称矩阵：

2.3 方阵行列式

n阶方阵：

2.4 共轭矩阵

3. 逆矩阵

3.1定义：

3.2 性质

• 唯一性：a的逆阵是唯一的

• 如何求逆：

• 运算规律：

3 矩阵分块化

3.1 块对角方阵

• 对角线的子块都是方阵

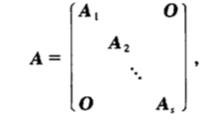
• 性质：

• 线性方程组：

克拉默法则：