- 图(graph)是由结点集合及结点间的关系集合组成的一种数据结构。图中的结点又称为顶点,结点之间的关系称为边(edge)。一个图G 记作
G=(V, E)
其中,V 是顶点A 的有限集合,E 是边的有限集合。即
V ={A|A∈某个数据元素集合}
E={(A,B )|A,B∈V } 或 E={〈A,B〉|A,B∈V且Path(A,B) }
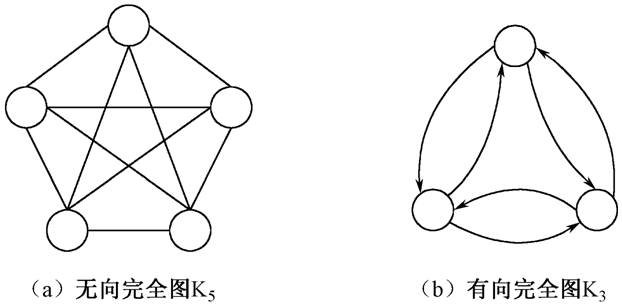
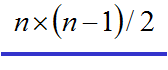 条边。
条边。
- 无向边和顶点关系
若(A,B)是一条无向边,则称顶点A和B互为邻接点(adjacent vertex)。边(A,B)与顶点A和B相关联。 - 有向边和顶点关系
若<A,B>是一条有向边,则称顶点A邻接到顶点B或顶点B邻接自顶点A。边<A,B>与顶点A和B相关联。 - 2.顶点的度
(1)无向图中顶点v的度(Degree)
无向图中顶点v的度是跟该顶点相关联的边的数目,记为deg(v)。
(2)有向图顶点v的入度(InDegree)
有向图中,以顶点v为终点的边的数目称为v的入度,记为indeg(v)。
(3)有向图顶点v的出度(Outdegree)
有向图中,以顶点v为起点的边的数目,称为v的出度,记为outdeg(v)
(4)有向图中,顶点v的度定义为该顶点的入度和出度之和,即deg(v)=indeg(v)+outdeg(v)。 -
度数和边数的关系
-
-
3、子图设G=(V,E)是一个图,若V'是V的子集,E'是E的子集,且E'中的边所关联的顶点均在V'中,则G'=(V',E')也是一个图,并称其为G的子图(Subgraph)。
若G' ≠G,称G'为G的真子图。
若G'为G的子图,且V' =V,称G'为G的生成子图。 -
-
- 4、路径(Path)
(1)无向图的路径
在无向图G中,若存在一个顶点序列vp,vi1,vi2,…,vim,vq,使得(vp,vi1),(vi1,vi2),…,(vim,vq)均属于E(G),则称顶点vp到vq存在一条路径。(2)有向图的路径
在有向图G中,路径也是有向的,它由E(G)中的有向边<vp,vi1>,<vi1,vi2>,…,<vim,vq>组成。(3)路径长度
- 对于不带权图,路径长度定义为该路径上边的数目。
- 对于带权图,路径长度定义为该路径上各边的权值之和。
(4)简单路径
若一条路径上除了vp和vq可以相同外,其余顶点均不相同,则称此路径为一条简单路径。
【例】在图G2中顶点序列v1,v2,v3,v4是一条从顶点v1到顶点v4的长度为3的简单路径
【例】在图G2中,顶点序列v1,v2,v4,v1,v3是一条从顶点v1到顶点v3的长度为4的路径,但不是简单路径;(5)回路
起点和终点相同(vp=vq)且长度大于1的简单路径称为回路。
【例】图G2中,顶点序列v1,v2,v4,v1是一个长度为3的回路【例】有向图G1中,顶点序列v1,v2,v1是一长度为2的回路。 -
5、连通性
(1)连通图和连通分量(i)顶点间的连通性
在无向图G中,若从顶点vi到顶点vj有路径(当然从vj到vi也一定有路径),则称vi和vj是连通的。(ii)连通图
若V(G)中任意两个不同的顶点vi和vj都连通(即有路径),则称G为连通图。(iii)连通分量
无向图G的极大连通子图称为G的连通分量。注意:
① 任何连通图的连通分量只有一个,即是其自身
② 非连通的无向图有多个连通分量。 -
(2)强连通图和强连通分量
(i)强连通图
有向图G中,若对于V(G)中任意两个不同的顶点vi和vj,都存在从vi到vj以及从vj到vi的路径,则称G是强连通图。(ii)强连通分量
有向图的极大强连通子图称为G的强连通分量。
注意:
① 强连通图只有一个强连通分量,即是其自身。
② 非强连通的有向图有多个强连分量。 - 1.2 图抽象数据类型
ADT Graph<T> //图抽象数据类型 { int vertexCount() //顶点数 T getVertex(int i) //顶点vi元素 void setVertex(int i, T x) //设置vi顶点为x int insertVertex(T x); //插入顶点 void removeVertex(int v) //删除顶点 int next(int i, int j); //后继邻接顶点 void insertEdge(int i, int j, int weight) //插入边 void removeEdge(int i, int j) //删除边 int weight(int i, int j) //边的权值 }
-
2 图的表示和实现 -
2.1图的邻接矩阵表示和实现
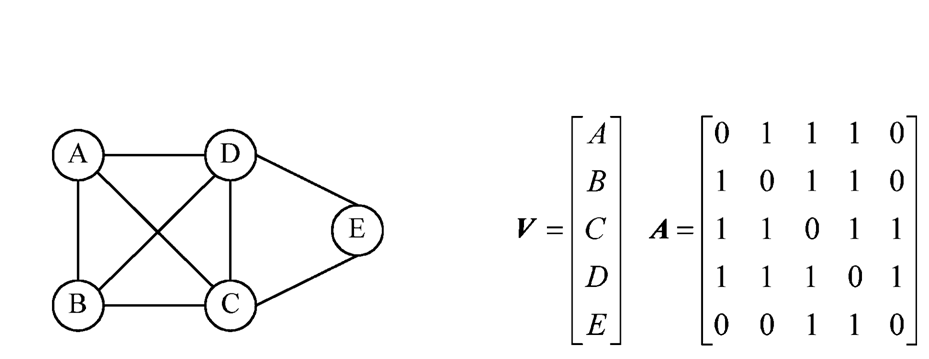
1、邻接矩阵(Adacency Matrix)
(1)不带权图的邻接矩阵 -
-
-
-
n无向图的邻接矩阵是对称的,有向图的邻接矩阵不一定对称。n从邻接矩阵可知顶点的度。
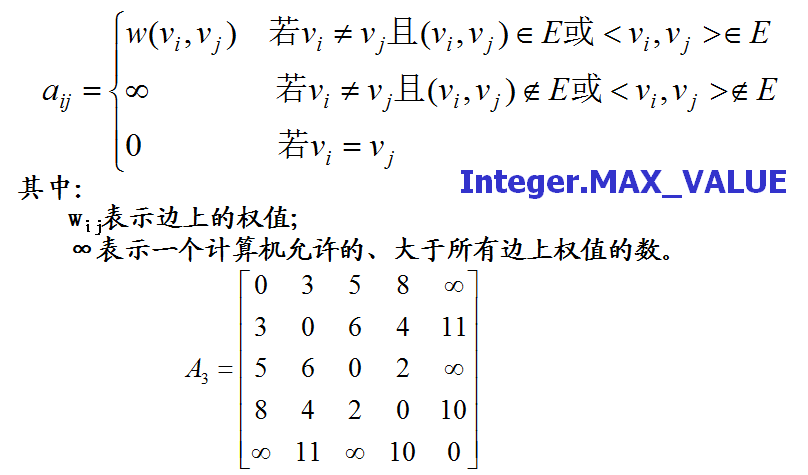
(2)带权图的邻接矩阵
若G是网络,则邻接矩阵可定义为: -
-
邻接矩阵的性质:
- 1.图中各顶点序号确定后,图的邻接矩阵是唯一确定的;
- 2.无向图和无向网的邻接矩阵是一个对称矩阵;
- 3.无向图邻接矩阵中第i行(或第i列)的非0元素的个数即为第i个顶点的度;
- 4.有向图邻接矩阵第i行非0元素个数为第i个顶点的出度,第i列非0元素个数为第i个顶点的入度,第i个顶点的度为第i行与第i列非0元素个数之和;
- 5.无向图的边数等于邻接矩阵中非0元素个数之和的一半,有向图的边数等于邻接矩阵中非0元素个数之和
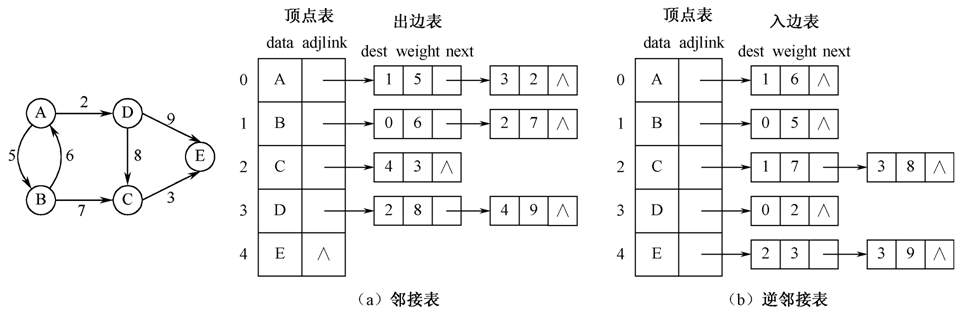
- 2.2图的邻接表表示和实现
-
- 1、邻接表(Adacency List)
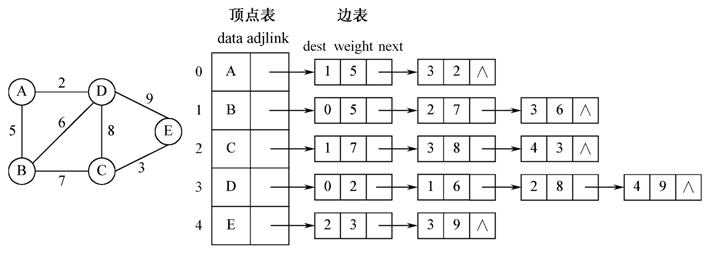
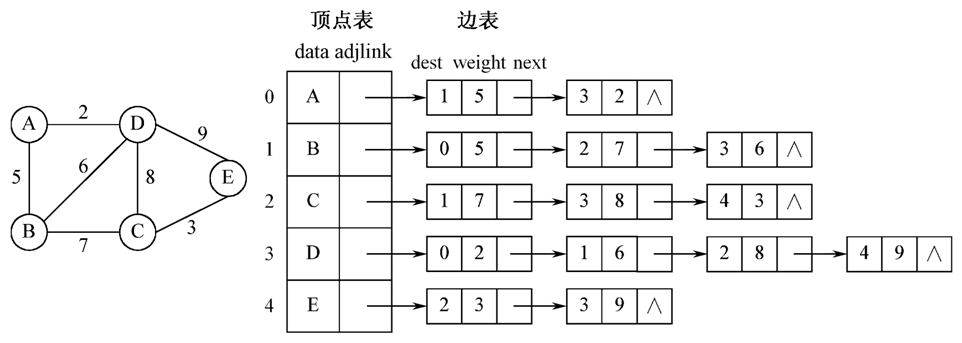
n图的邻接表表示由顶点表和边表组成n顶点表以顺序表存储图中所有顶点元素n边表以单链表存储与顶点相关联的多条边。
-
- 顶点表中的结点结构
- 边表中的结点结构
- (1)无向图的邻接表表示
- (2)有向图的邻接表表示
- 邻接表的性质:
-
- 1.图的邻接表表示不是唯一的,它与表结点的链入次序有关;
- 2.无向图的邻接表中第i个边表的结点个数即为第i个顶点的度;
- 3.有向图的邻接表中第i个出边表的结点个数即为第i个结点的出度,有向图的逆邻接表中第i个入边表的结点个数即为第i个结点的入度;
- 4.无向图的边数等于邻接表中边表结点数的一半,有向图的边数等于邻接表(逆邻接表)中出边表结点(入边表结点)的数目。
- 如何选择图的这两种存储结构呢?
-
- 一个有n个顶点、e条边的图G:
- 当n较小且e较大时,采用邻接矩阵存储效率较高;
- 当n较大且e《n时,采用邻接表存储效率较高;
- 3图的遍历
n从图中某个顶点出发访问图中所有顶点,且使得每一顶点仅被访问一次,这一过程称之为图的遍历。l指定遍历的第一个访问结点。l由于一个顶点可能与多个顶点相邻,因此要在多个邻接顶点之间约定一种访问次序。l由于图中可能存在回路,在访问某个顶点之后,可能沿着某条路径又回到该顶点。因此,为了避免重复访问同一顶点,在遍历过程中必须对访问过的顶点做标记(visited数组)。1 图的深度优先搜索遍历
1.图的深度优先搜索
- 图G的初态是所有顶点均未曾访问过。在G中任选一顶点v为出发点(源点),则深度优先遍历可定义如下:
- 首先访问出发点v,并将其标记为已访问过;
- 然后依次从v出发按照某种约定好的顺序搜索v的每个邻接点w。若w未曾访问过,则以w为新的出发点继续进行深度优先遍历,直至图中所有和源点v有路径相通的顶点(亦称为从源点可达的顶点)均已被访问为止。
- 若此时图中仍有未访问的顶点,则另选一个尚未访问的顶点作为新的源点重复上述过程,直至图中所有顶点均已被访问为止。
- 图的深度优先遍历类似于树的先根遍历。采用的搜索方法的特点是尽可能先对纵深方向进行搜索。
2 图的广度优先搜索遍历1、广度优先遍历定义
图G的初态是所有顶点均未访问过。在G中任选一顶点v为源点,则广度优先遍历可以定义为:- 首先访问出发点v,接着依次访问v的所有邻接点w1,w2,…,wt,
- 然后再依次访问与w1,w2,…,wt邻接的所有未曾访问过的顶点。依此类推,直至图中所有和源点v有路径相通的顶点都已访问到为止。此时从v开始的搜索过程结束。
- 若G是连通图,则遍历完成;否则,在图G中另选一个尚未访问的顶点作为新源点继续上述的搜索过程,直至G中所有顶点均已被访问为止。
广度优先遍历类似于树的按层次遍历。采用的搜索方法的特点是尽可能先对横向进行搜索。
- 对于一个连通(无向)图或一个强连通(有向)图,从任何一个顶点出发的一次遍历,可以访问图中的每个顶点。
- 对于一个非连通(无向)图,从一个顶点出发的一次遍历,只能访问图中的一个连通分量。
- 4 最小生成树
- 1生成树
1、树
-
- 连通的无回路的无向图称为无向树,简称树(tree)。树中的悬挂点又称为树叶(leaf),其他结点称为分支点(branched node)。
-
树中无回路。若去掉树中的任意一条边,则树变为森林,成为非连通图;若给树加上一条边,则形成一条回路,则不是树。2、生成树和生成森林
- 如果连通图G的一个子图是一棵包含G的所有顶点的树,则该子图称为G的生成树。
生成树是连通图的包含图中的所有顶点的极小连通子图。
- 如果一个无向图是非连通图,则其每一个连通分量都可以生成一颗树,这些树将组成该图的生成森林。
- 图的生成树和生成森林不惟一。从不同的顶点出发进行遍历,可以得到不同的生成树或生成森林。
- 深度优先生成树和广度优先生成树
-
- 设图G=(V,E)是一个具有n个顶点的连通图。则从G的任一顶点(源点)出发,作一次深度优先搜索(广度优先搜索),搜索到的n个顶点和搜索过程中从一个已访问过的顶点vi搜索到一个未曾访问过的邻接点vj,所经过的边(vi,vj)(共n-1条)组成的极小连通子图就是生成树。(源点是生成树的根)
- 通常,由深度优先搜索得到的生成树称为深度优先生成树,简称为DFS生成树;
- 由广度优先搜索得到的生成树称为广度优先生成树,简称为BFS生成树。
- 生成树中任意两个顶点之间只有唯一的一条路径。
-
- 1生成树
- 1、邻接表(Adacency List)
-
-
-
-
-
- 3、最小生成树
- 2 最小生成树的构造算法
MST性质
-
- 最小生成树性质:设G=(V,E)是一个连通网络,U是顶点集V的一个真子集。若(u,v)是G中所有的一个端点在U(u∈U)里、另一个端点不在U(即v∈V-U)里的边中,具有最小权值的一条边,则一定存在G的一棵最小生成树包括此边(u,v)。
- 为方便说明,先作以下约定:
-
①将集合U中的顶点看作是红色顶点;
②而V-U中的顶点看作是蓝色顶点;
③连接红点和蓝点的边看作是紫色边;
④权最小的紫边称为轻边(即权重最“轻”的边)。
于是,MST性质中所述的边(u,v)就可简称为轻边。 - 1、普里姆(Prim)算法
算法思想:
T=(U,TE)是存放MST的集合。
①T的初值是({r}, )
即最小生成树初始时只有一个红点r,没有红边。②T经过n-1次如下步骤操作,最后得到一棵含n个顶点,n-1条边的最小生成树
-
- 选择紫边集中一条轻边并扩充进T
- 将轻边连接的蓝点改红点
- 将轻边改红边
- 修改紫边集
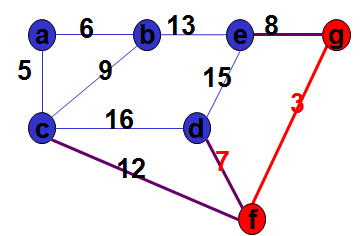
- 2、克鲁斯卡尔(Kruskal)算法
算法思想
①T的初始状态
只有n个顶点而无边的森林T=(V, )
②按边长递增的顺序选择E中的n-1安全边(u,v)并加入T,生成MST
注意:
- 安全边指两个端点分别是森林T里两棵树中的顶点的边。加入安全边,可将森林中的两棵树连接成一棵更大的树
- 因为每一次添加到T中的边均是当前权值最小的安全边,MST性质也能保证最终的T是一棵最小生成树。
- 5最短路径
1. 最短路径
- 最短路径问题,即求两个顶点间长度最短的路径
- 路径长度不是指路径上边数的总和,而是指路径上各边的权值总和
- 单源最短路径问题:对于给定的有向网络G=(V,E)及单个源点v,求从v到G的其余各顶点的最短路径。
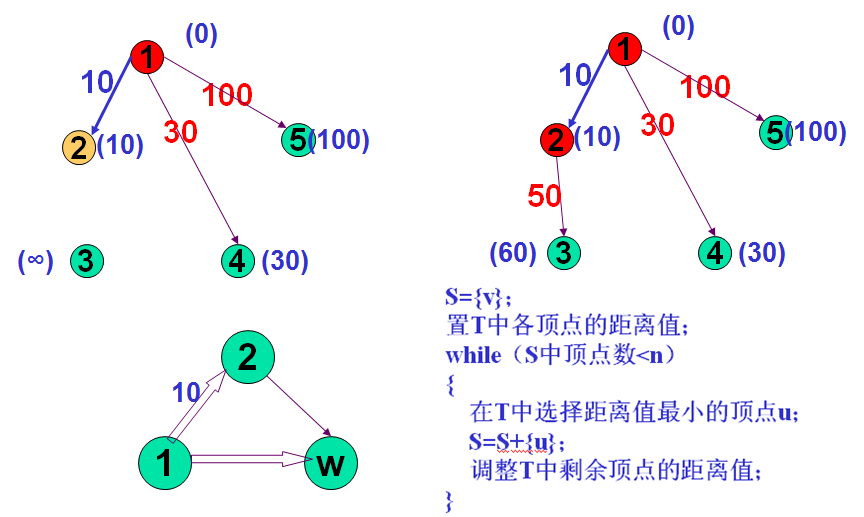
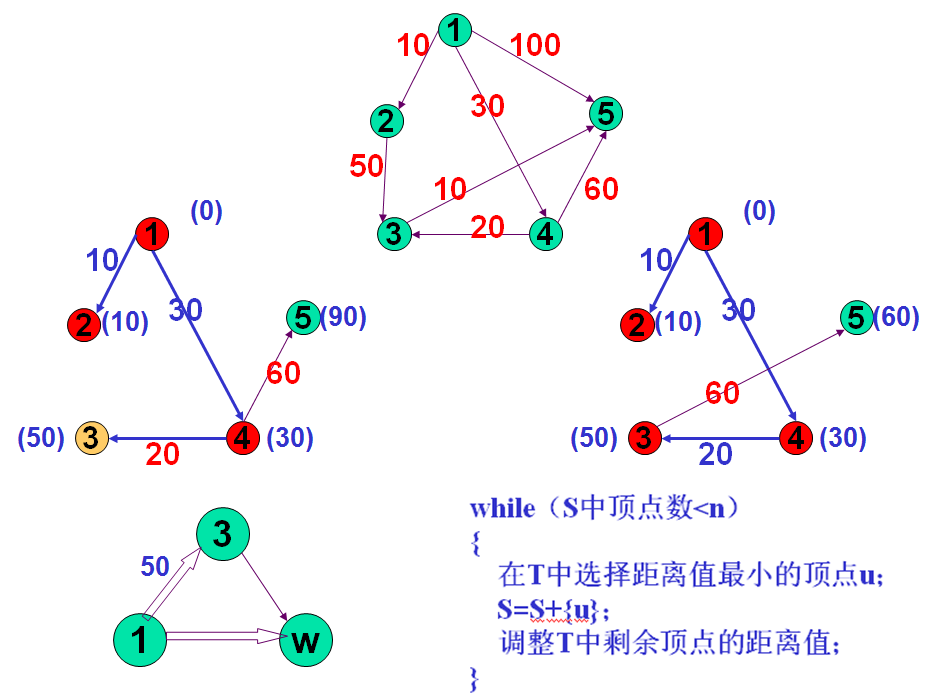
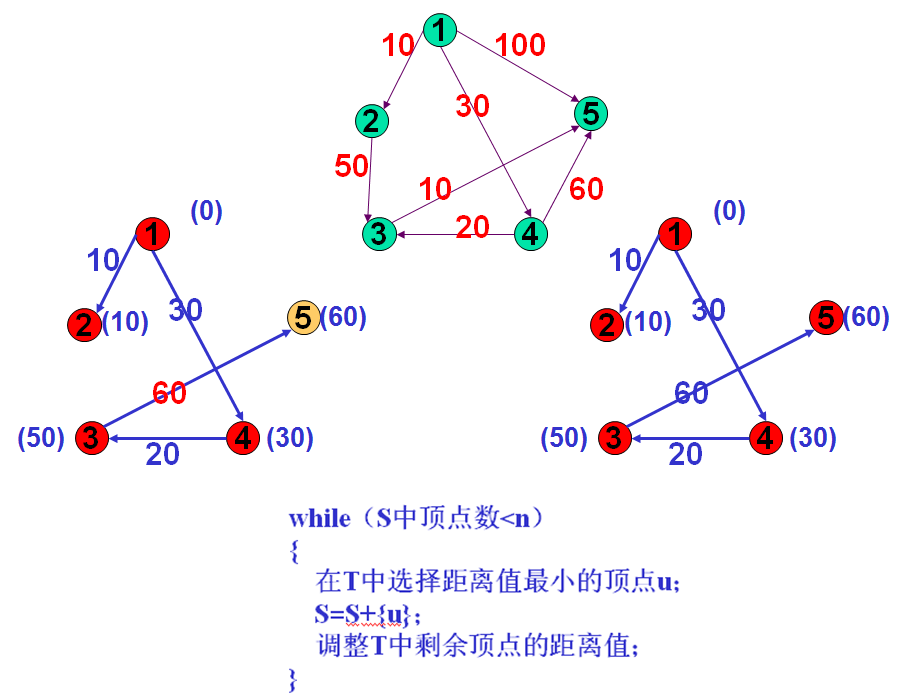
- 迪卡斯特拉(Dijkstra)算法基本思想:
-
S={v};
置T中各顶点的距离值;
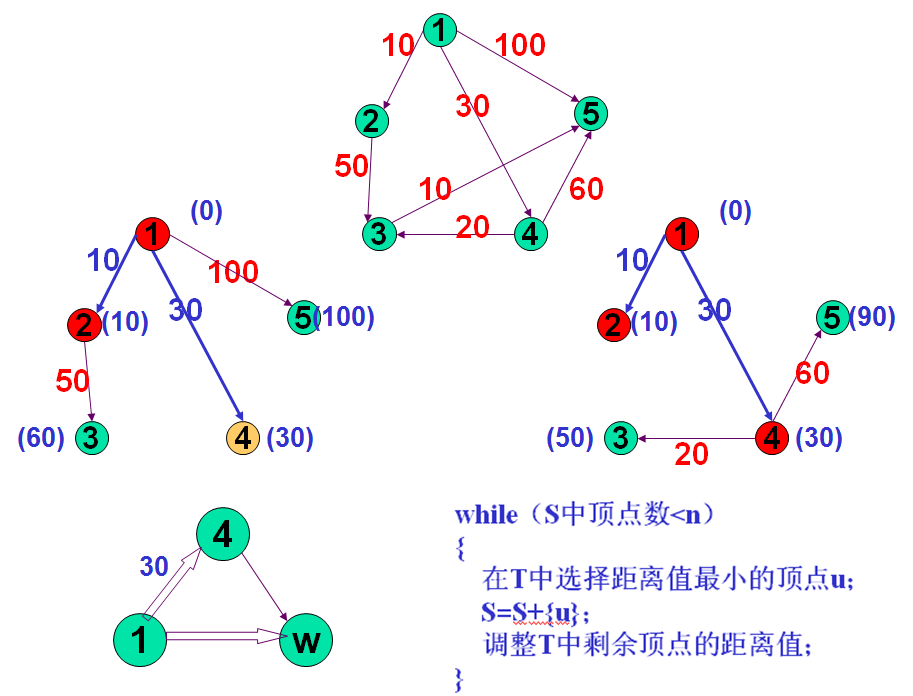
while(S中顶点数<n)
{
在T中选择距离值最小的顶点u;
S=S+{u};
调整T中剩余顶点的距离值;
}
调整距离的原则是:当u的最短路径长度与u到T中的顶点之间的权值之和小于该顶点的当前最短路径长度时,用前者替换后者。 -
-
每对顶点间的最短路径(Floyd算法)
-
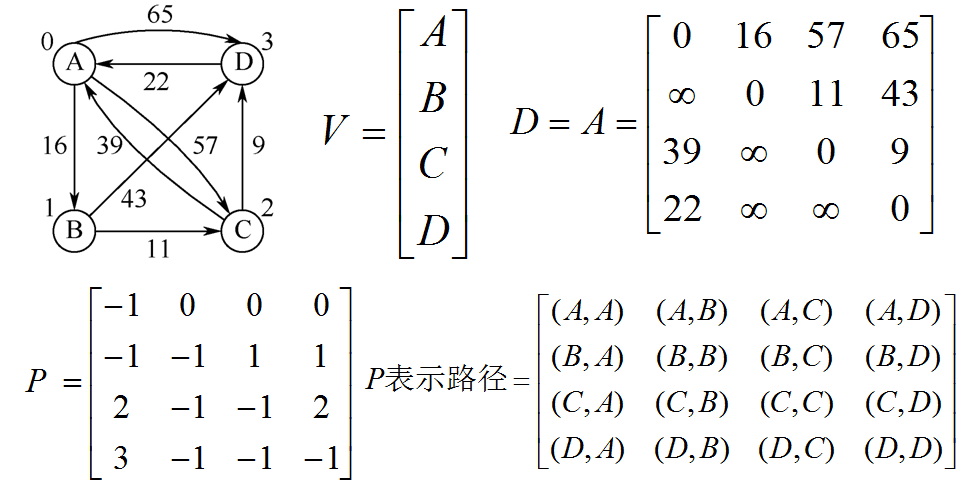
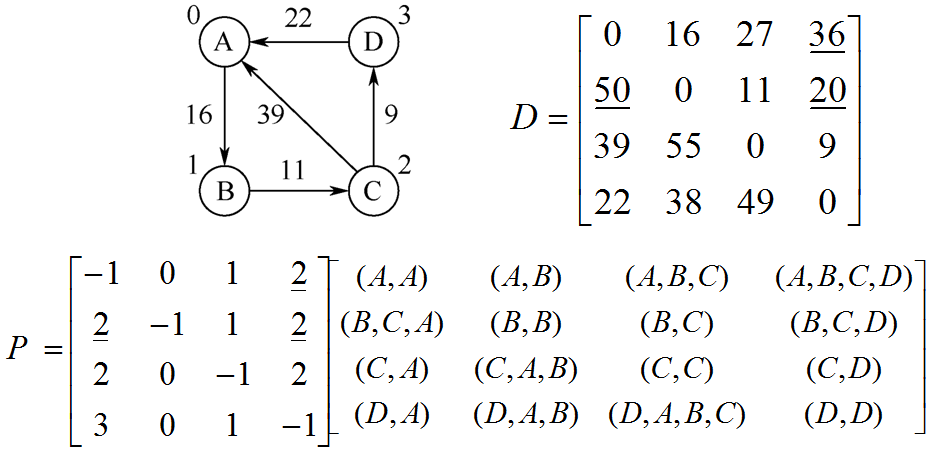
2. Floyd算法描述
-
(1)矩阵初值
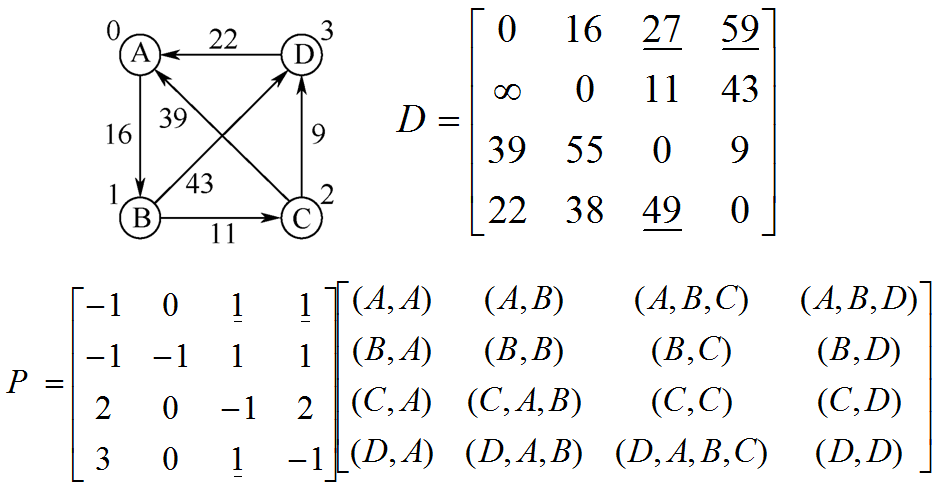
- (2)迭代
if ( ) // 长度小于
{
; // 长度替换为更短
; // 经过的最后一个顶点,
替换为 经过的最后一个顶点
} -
② 以B作为其他路径的中间顶点 -
③ 以C作为其他路径的中间顶点
- ④ 以D作为其他路径的中间顶点
-
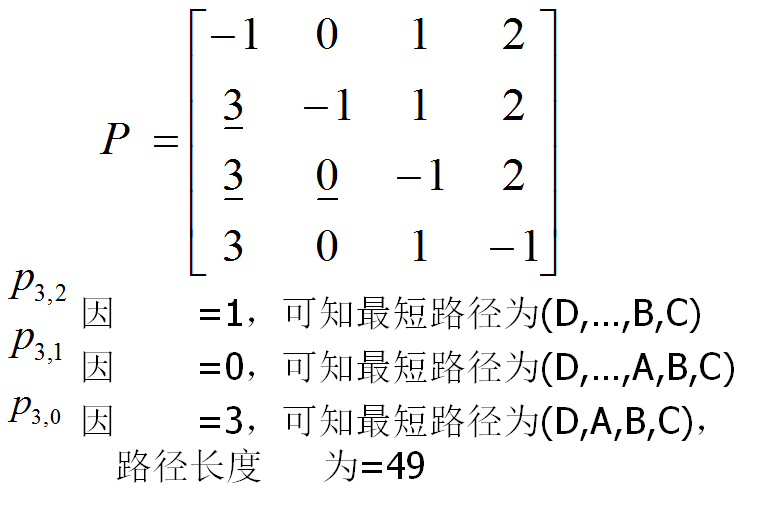
(3)获得每条最短路径
- 3、最小生成树
-
-
-
-









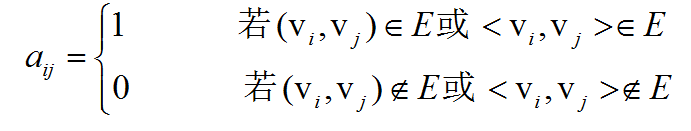

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








