100以内偶数之积

 今天看到一个题让求1到100之内偶数之积（自己没学过算法，萌新一枚，大佬路过请多加指点），unsigned long long   int 类型已经装不下了，虽然unsigned  long  double   类型还可以继续装下，但如果让求1000以内甚至更高的话，那显然没有任何一个类型可以正常运算。下面是错误示例代码：

#include<iostream>
using namespace std;
int main()
{
	unsigned long long int x = 1;
	for (int i = 2; i < 101; i = i + 2)
	{
		x = x * i;
	}
	cout << x;
	system("pause");
	return 0;
}

运行结果：

正常相乘显然是不能够得到正确答案的，这时候我们就应该想到用字符串或者数组来存储这个结果，同时也应该用字符串或者数组来进行运算。那怎么进行运算呢，笔算乘法给了我们一个完美的解决方法：

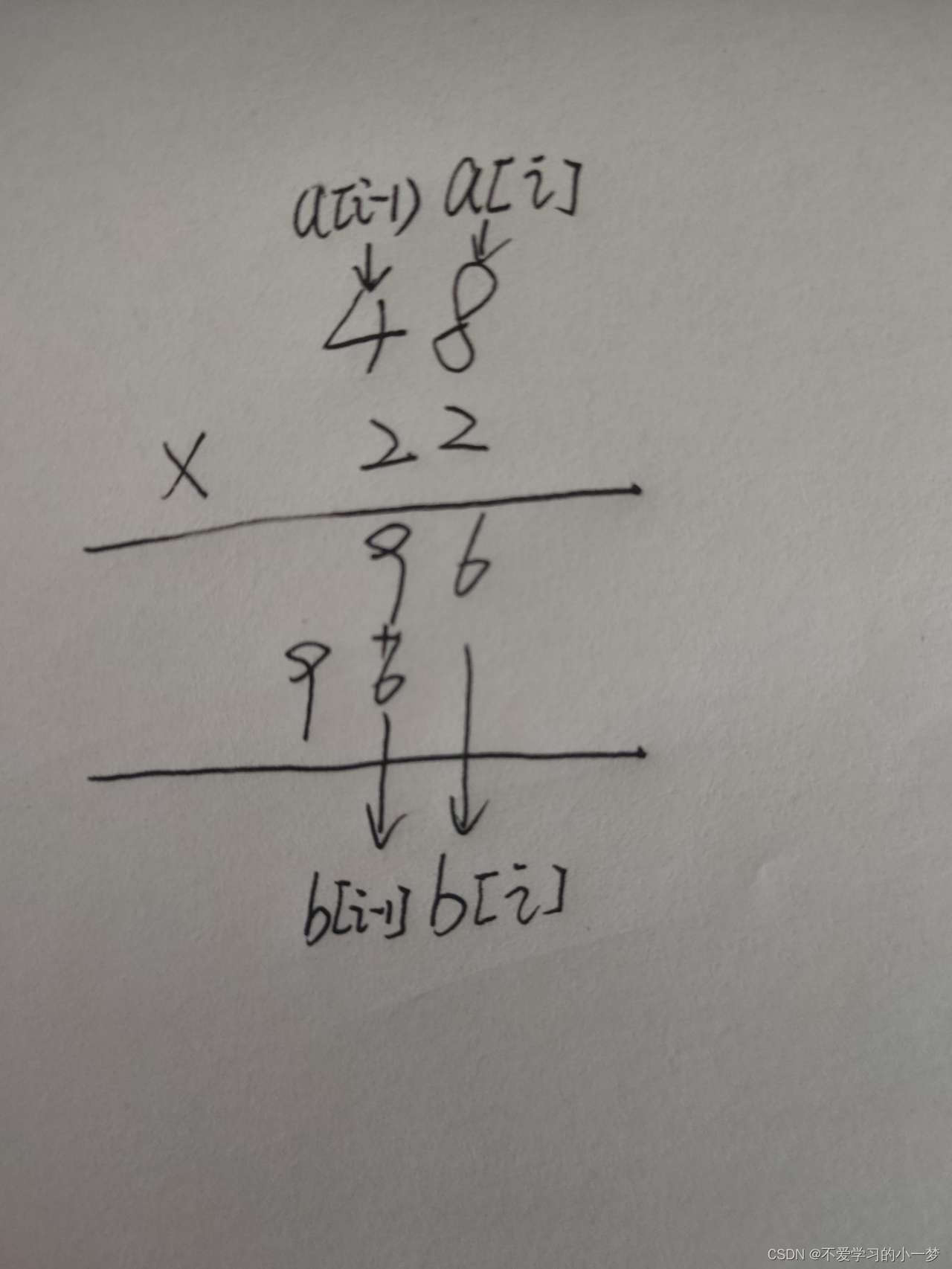
我们只需要将每一次计算后的值都存放在结果数组中，然后用数组每一位分别跟要相乘的数作乘（就不会发生乘的结果超出类型范围的错误，就算是算到几万以内的偶数积用int也远远足够了）。接下来要处理的就是这样相乘之后如何继续进行对应位相加得到每一次相乘之后的最终结果然后将结果存储到结果数组中。我的处理方法是再定义一个数组来存储每一位的值（每一位的值由相乘后对位相加得到）。注意：想要一次性全部对位相加需要低位补0，同样会出现范围爆炸错误，这时候应该将每一位相乘的结果按照对应位放到数组中再进行每一位的相加就不会数据爆炸了。

for (int i = 999; i > 0; i--)
	{
		int t = a[i] * x;
		int temp = digits_x(t);//t的位数为temp
		for (int j = i; j > i - temp; j--)//将每一位之和存储在b数组中
		{
			b[j] = b[j] + t % 10;
			t = t / 10;
		}
	}

然后就要解决进位问题，数组某一位大于10就要向前进位（进位数为该位的值除以10，就算该位的值超过3位依旧成立）。然后将得到的数组再复制给结果数组进行下一次相乘，循环下去就能得到最终结果了。

void carry_bit(int b[])//进位运算
{
	for (int i = 999; i > 0; i--)
	{
		if (b[i] >= 10)
		{
			b[i - 1] = b[i-1]+b[i] / 10;
			b[i] = b[i] % 10;
		}
	}
}

最后因为我们是从数组的最后一位开始计算的，所以数组的前面会有很多位为0，我们需要先找到有效位再进行结果的输出。完整代码如下：

#include<iostream>
using namespace std;
int b[1000] = {0};
int n10(int n) //返回10的n次方值
{
	int n10=1;
	for (int i = 0; i < n; i++)
	{
		n10 = n10 * 10;
	}
	return n10;
}
int digits_x(int x)//返回x为几位数
{
	int n = 1;
	while (n10(n) <= x)n++;
	return n;
}
void carry_bit(int b[])//进位运算
{
	for (int i = 999; i > 0; i--)
	{
		if (b[i] >= 10)
		{
			b[i - 1] = b[i-1]+b[i] / 10;
			b[i] = b[i] % 10;
		}
	}
}
void Mul(int a[], int x)//一次相乘
{
	for (int i = 999; i > 0; i--)
	{
		int t = a[i] * x;
		int temp = digits_x(t);//t的位数为temp
		for (int j = i; j > i - temp; j--)//将每一位之和存储在b数组中
		{
			b[j] = b[j] + t % 10;
			t = t / 10;
		}
	}
	carry_bit(b);//进位
	for (int i = 0; i < 1000; i++)//将b数组值复制给a数组
	{
		a[i] = b[i];
	}
	for (int i = 0; i < 1000; i++)//b数组置0
	{
		b[i] = 0;
	}
}

int main()
{
	int a[1000] = { 0 };
	a[999] = 2 ;
	for (int i = 4; i <101 ; i=i+2 )//累乘
	{
		Mul(a, i);
	}
	for (int i = 0; i <1000; i++)//寻找有效位之后开始打印结果
	{
		if (a[i] > 0)
		{
			for (int j = i; j < 1000; j++)
			{
				cout << a[j];
			}
			break;
		}

	}
	system("pause");
	return 0;
}

运行结果：

 

这样包括计算很多数连续相乘，很大的数的阶乘的时候同样可以解决了。当然这只是一个没有学过算法的萌新自己琢磨的，复杂度还是偏高的（肯定有更加好的方法），但对于刚接触的朋友来说应该还是有所帮助的，如果有大佬路过的话请指教指教（膜拜）。