3.31东莞特长生2013

分数

100+100+0+100=300

一、成绩排序

问题描述：

小明是希望中学某班的信息科代表，班里刚买了新电脑只有操作系统还没有装办公软件。老师急着要将该班的语文测验成绩按从高到低排序。小明找到了好朋友你，幸好你带了编程工具。现在请你编一个程序帮助小明的班主任将他们班的语文成绩按从高到低排序。

数据输入：

文件共有N+1行，第一行为一个正整数N，表示共有N个成绩（1=

数据输出：

共有N行，每行一个正整数。输出按从高到低排好序的结果。

输入输出样例：

score.in
5
90
105
87
65
98
score.out
105
98
90
87
65

题解

随便排排就好

#include <cstdio>
#include <algorithm>
#include <cstring>

using namespace std;

int main()
{
    freopen("score.in","r",stdin);
    freopen("score.out","w",stdout);
    int n,a[555];
    scanf("%d",&n);
    memset(a,0,sizeof(a));
    for (int i=1;i<=n;i++)
        scanf("%d",&a[i]);
    sort(a+1,a+1+n);
    for (int i=n;i>=1;i--)
        printf("%d\n",a[i]);
}

二、数对

问题描述：

考虑一组n个不同的正整数a1,a2,…,am，它们的值在1到1000000之间。给定一个整数x。写一个程序sumx计算这样的数对个数(ai,aj)，1<=i

数据输入：

标准输入的第一行是一个整数n(1<=n<=1000000)。第二行有n个整数表示元素。第三行是一个整数x(1<=x<=2000000)。

数据输出：

输出一行包含一个整数表示这样的数对个数。

注意：对于50%的测试数据，n<=1000。

输入输出样例：

sumx.in
9
5 12 7 10 9 1 2 3 11
13
sumx.out
3

解释：不同的和为13的数对是(12, 1), (10, 3)和(2, 11)。

题解

排一下序，然后对于每个数找是否存在与它之和为x的数，统计答案，输出答案/2.

#include <cstdio>
#include <algorithm>

using namespace std;

int b[1000007];

int main()
{
    freopen("sumx.in","r",stdin);
    freopen("sumx.out","w",stdout);
    int n,x,sum=0,y=0;
    scanf("%d",&n);
    for (int i=1;i<=n;i++)
    {
        int t;
        scanf("%d",&t);
        b[i]=t;
    }
    scanf("%d",&x);
    sort(b+1,b+1+n);
    for (int i=1;i<=n;i++)
    {
        int l=1,r=n,mid,c=0;
        while (l<=r)
        {
            mid=(l+r)/2;
            if (b[mid]+b[i]<=x) 
            {l=mid+1;c=mid;}else r=mid-1;
        }
        if (b[c]+b[i]==x&&c!=i)
        sum++;
    }
    printf("%d",sum/2);
}

三、数字编码（coding）

问题描述：

一列有顺序的非负整数，需要把它们编码成一个0、1字符串进行传送。设这一列数为P={P1，P2，…，Pn}，其中0<=Pi<32767，具体的编码方法为：把P分成k个段 S1，S2，…，Sk，在第i个段Si 中有a(i)个数字，且该段中每个数字都用b(i)位0、1串来编码表示，另外为了正确解码，还要在该段前面附加上一个消息头，用来指出该段有多少个数字以及每个数字的编码位数，消息头的格式规定如下：首先用8位二进制位表示a(i)，这导致0< a(i)<256，另外由于0<=Pi<32767，即序列中每个数字最多用15位0、1串编码，因此接着用4位二进制位表示b(i) 。因此Si段编码后需要8+4+a(i)*b(i)位。按此格式，序列{P1，P2，…，Pn}的编码总位数为a(1)*b(1)+a(2)*b(2)+…+a(k)*b(k)+12*k 位，不同的分段方式可能对应不同的编码位数。
例如，对数字序列{ 7，6，16，2，1，88，250，222}，其最优分段方式是分为2段{7，6，16，2，1}和{88，250，222}，a(1)=5，b(1)=5，a(2)=3，b(2)=8，所以该数字序列的最优编码位数为25+24+24=73位。
你的问题是对于给定的数字序序列，按照上述编码规则，求最小的编码位数。

数据输入：

包含n+1整数，其中第一个为正整数n (n<=30000)，表示序列的长度，之后是n个非负整数，表示待编码的数字序列。数与数之间用空格隔开。

数据输出：

只包含一个数，表示你计算出的最小编码位数。

输入输出样例：

coding.in
8 7 6 16 2 1 88 250 222
coding.out
73

题解

可以用动态规划。
又分两种办法：
类模拟的动规，这种的空间复杂度小很多，时间复杂度也和另一种相差不多，即我用的方法。
先预处理出每个数所需编码数。从后往前，f[i]表示编到第i个的最优解，max表示i到j之间最大编码数，每一个数都往后判断在哪里切最优，然后由最优解转移过来
f[i]=min(f[j]+12+max*(j-i))(j<=i+255,j<=n+1)

---

方法二
直接动规，f[i][j]表示编到第i位，切了j次

#include <cstdio>

using namespace std;

int a[30004],f[30004];

int min(int a,int b)
{
    if (a<b) return(a);
    return(b);
}

int main()
{
    int n;
    scanf("%d",&n);
    for (int i=1;i<=n;i++)
    {
        int t,e=0;;
        scanf("%d",&t);
        while (t>0)
        {
            e++;
            t=t>>1;
        }
        a[i]=e;
    }
    for (int i=n;i>=1;i--)
    {
        f[i]=f[i+1]+12+a[i];
        int max=a[i],cc=min(i+255,n+1);
        for (int j=i+2;j<=cc;j++)
        {
            if (a[j-1]>max) max=a[j-1];
            f[i]=min(f[i],f[j]+max*(j-i)+12);
        }
    }
    printf("%d",f[1]);
}

四、廉价最短路径

问题描述：

图是由一组顶点和一组边组成的。一条边连接两个顶点。例如，图1表示了一个有4个顶点V、5条边的图。图中，每条边e是有方向的，方向从起点到终点，并且每条边都有价值。用整数0,1,…,m-1可以表示一个有m个顶点的图。

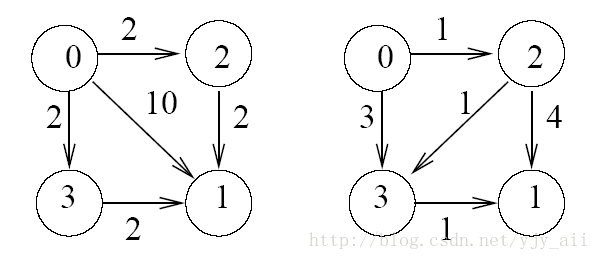
——————图1————————————-图2———————-
一条路径连接了一个点Vi和另一个点Vj，其方向与经过的一系列边的方向一致。路径的长度是途经边的条数，路径的费用是边价值的总和。对于一个给定的图，你的任务是在所有最短路径中，找出需要最少费用的连接V0和V1的路径。一个需要最少费用的最短路径称之为廉价最短路径。
让我们重新考虑图1，从0到1的最短路径是只含一条边的路径0→1，费用是10。当然，还有更便宜的路：0→2→1和 0→3→1，但是它们比第一条路径长(有2条边)。所以，0→1是廉价最短路径。
看一下另一个例子，图2，它有2条最短路径，其长度是2，路径0→3→1(费用=4)比路径0→2→1(费用=5)花费少。还用另一条路径0→2→3→1(费用=3)，虽然便宜但是很长。所以，廉价最短路径是0→3→1。

数据输入

输入文件第一行有两个整数m和n，用一个空格隔开，其中，m是顶点数，而n是边数。接下来的n行给出所有的边及其价值，每行有3个整数(相邻两个整数间有一个空格)，表示起点，终点和边的价值。顶点最多有100个，编号在0到99之间。边最多有1000条，其价值在0到215-1之间。

数据输出

输出文件仅有一行包含一个整数，即V0→V1的廉价最短路径的费用。当出现有多个廉价最短路径的情况时，它们的费用是一样的。

输入输出样例

paths.in
4 5
0 2 2
0 3 2
0 1 10
2 1 2
3 1 2

paths.out
10

题解

最短路，随便用一个算法就好
一边找最短路一边判断费用即可

#include <cstdio>
#include <cstring>

using namespace std;

int ls[102],ne[1003],y[1003],w[1003],d[102];
long long c[102],e;

void spfa()
{
    int h=0,t=1;
    int v[2003],b[102];
    memset(c,0x7f,sizeof(c));
    memset(d,0x3f,sizeof(d));
    memset(b,0,sizeof(b));
    v[1]=1;b[1]=1;c[1]=0;d[1]=0;
    while (h<t)
    {
        h++;
        int j=ls[v[h]];
        while (j>0)
        {
            int x=v[h],z=y[j];
            if (d[x]+1<d[z]||(d[x]+1==d[z]&&c[x]+w[j]<c[z]))
            {
                d[z]=d[x]+1;
                c[z]=c[x]+w[j];
                if (!b[z])
                {
                    t++;
                    v[t]=z;
                    b[z]=1;
                }
            }
            j=ne[j];
        }
        b[v[h]]=0;
    }
}

int main()
{
    freopen("paths.in","r",stdin);
    freopen("paths.out","w",stdout);
    int n,m,ans=0;
    scanf("%d%d",&n,&m);
    for (int i=1;i<=m;i++)
    {
        int a,b,c;
        scanf("%d%d%d",&a,&b,&c);
        a++;b++;
        ne[i]=ls[a];ls[a]=i;y[i]=b;w[i]=c;
    }
    spfa();
    printf("%d",c[2]);
}