机器学习—决策边界

为了更好的理解逻辑回归，计算它的预测来回顾，下图如何以Logistic回归模型的输出分两步计算，第一步中，将z=w*x+b,将sigmoid函数g应用于这个值z，这是Z状结肠函数的公式。如果你把Z状结肠函数的定义插入Z的定义，然后你会发现如右图所示的函数，这类似于上篇文章中的函数，可能是0.7或0.3，如果你想让学习算法预测，y的值是0还是1，设置一个阙值，在这个阙值之上你预测y=1，或者将预测设置为=1，下边的预测=0，所以一个常见的选择是选择0.5的阙值，所以如果f(x)>=0.5,那么预测y=1或者如果f(x)<=0.5,那么预测值=0。

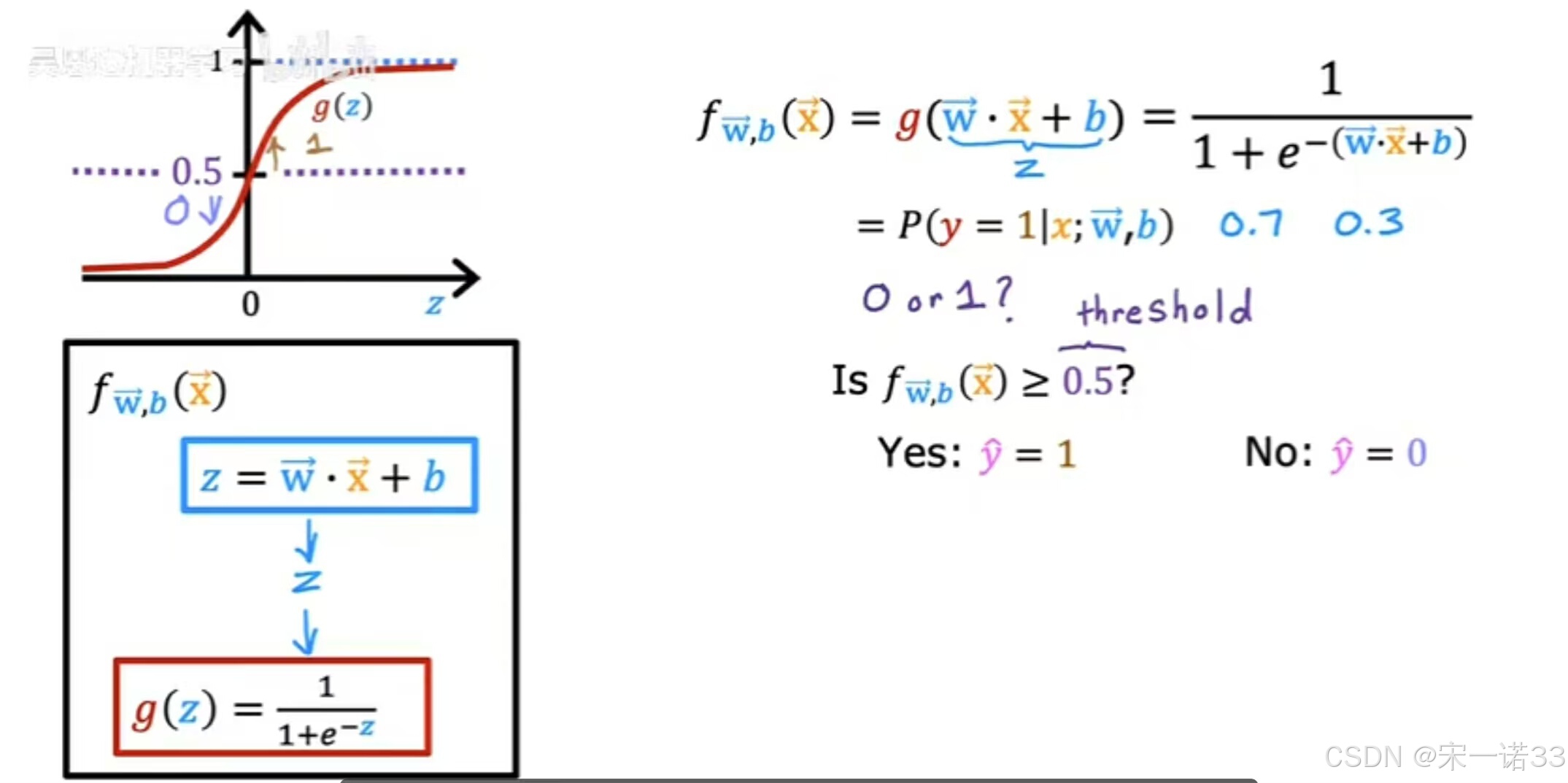
当f(x)>=0.5，即g(z)>=0.5,此时有一个Z状结肠函数。所以g(z)>=0.5,当z>=0时，只要z在轴的右半部分，最后当z＞或=0时，Z=W*X+b，所以z>=0，即W*X+b>=0，所以总结一下，无论何时w点，模型都预测了一个X+b>=0,反过来说，当W*X+b<0时，算法预测y=0

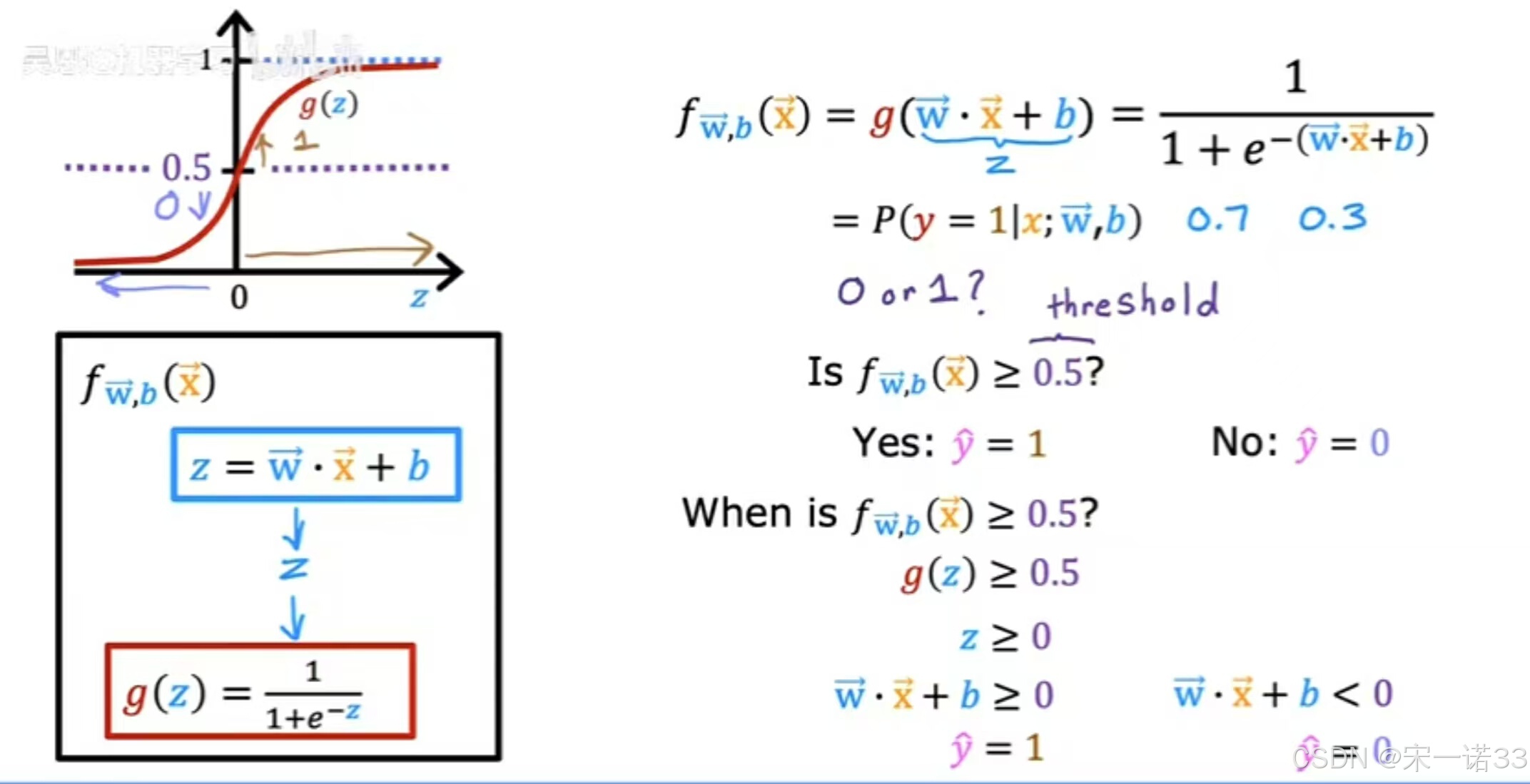
所以考虑到这一点，现在让我们可视化模型是如何做出预测的

举一个分类问题的例子，其中有两个特性X1和X2，而不仅仅是一个功能，还有一个训练集，小红叉代表积极的例子，蓝色的小圆圈代表否定的例子，所以红叉对应y=1，蓝色的圆圈对应的y=0,Logistic回归模型将使用该函数进行预测，f(x)=g(z)=g(W1X1+W2X2+b),因为我们有两个特点，X1和X2，参数的值为W1=1,W2=1,b=-3,让我们看看Logistic回归是如何做出预测的，尤其是算出wx+b>=0时，当wx+b<0时，有一条非常有趣的线可以看，即wx+b=0，原来这条线也叫决策边界，因为在这条线上几乎是中立的，现在y=0还是y=1，对于参数W1的值，我们在下面写了两个，这个判定边界是X1+X2-3，所以当它=0时，对应的线X1+X2=3，就是紫色的线，所以这条线就是决策边界。如果特征X在这条线的右侧，逻辑回归可以预测，在这条线的左边，逻辑回归预测为零。换句话说，我们刚才看到的是逻辑回归的决策边界，当参数W1=1时，W2=1，b=-3，如果你有不同的参数选择，决策边界现在将是一条不同的线。

下面看一个更复杂的例子

决策边界不再是直线，和前边一样，十字表示类y=1，小圆圈表示类y=0，我们已经了解了如何在线性回归中使用多项式，那么也可以在逻辑回归中做同样的事情，所以把Z=W1*X1²+W2*X2²+b,将多项式特征转化为Logistic回归，假设我们最终选择W1=1,W2=1,b=-1,所以Z=X1²+X2²-1，当Z=0时，前面的判定边界将对应于，所以这个表达式=0，当X1²+X2²=1，如果你在下边的图表上画，对应X1²+X2²=1的曲线是这个圆圈，当X1²+X2²>=1时，那是圆圈外的这个区域，就在那时你预测y是1，当X1²+X2²<1时那是圆圈内的这个区域，你预测y=0。

比这些更复杂的决策边界

通过使用更高阶的多项式来做到这一点，Z=W1X1+W2X2+W3X1²+W4X1X2+W5X2²，然后你可能会得到更复杂的决策边界，该模型可以定义决策边界，比如这个例子和这样的椭圆，或者使用不同的参数选择，甚至可以得到更加复杂的决策边界，可能看起来像这样的函数，所以这是一个更复杂的决策边界的例子，比我们之前看到的，这个Logistic回归的实现将预测这个形状内的y=1,在这个形状外预测y=0，所以有了这些多项式特征，可以得到更复杂的决策边界。逻辑回归可以学习拟合相当复杂的数据，尽管如果你不包括这些高阶多项式，所以如果你使用的唯一特性是X1，X2,X3，以此类推，那么Logistic回归的决策边界总是线性的，永远是一条直线。