蓝桥杯 算法训练 Lift and Throw

问题描述

　　给定一条标有整点(1, 2, 3, …)的射线. 定义两个点之间的距离为其下标之差的绝对值.
　　Laharl, Etna, Flonne一开始在这条射线上不同的三个点, 他们希望其中某个人能够到达下标最大的点.
　　每个角色只能进行下面的3种操作, 且每种操作不能每人不能进行超过一次.
　　1.移动一定的距离
　　2.把另一个角色高举过头
　　3.将举在头上的角色扔出一段距离
　　每个角色有一个movement range参数, 他们只能移动到没有人的位置, 并且起点和终点的距离不超过movement range.
　　如果角色A和另一个角色B距离为1, 并且角色B没有被别的角色举起, 那么A就能举起B. 同时, B会移动到A的位置,B原来所占的位置变为没有人的位置. 被举起的角色不能进行任何操作, 举起别人的角色不能移动.同时, 每个角色还有一个throwing range参数, 即他能把举起的角色扔出的最远的距离. 注意, 一个角色只能被扔到没有别的角色占据的位置. 我们认为一个角色举起另一个同样举起一个角色的角色是允许的. 这种情况下会出现3个人在同一个位置的情况. 根据前面的描述, 这种情况下上面的两个角色不能进行任何操作, 而最下面的角色可以同时扔出上面的两个角色. 你的任务是计算这些角色能够到达的位置的最大下标, 即最大的数字x, 使得存在一个角色能够到达x.

输入格式

　　输入共三行, 分别为Laharl, Etna, Floone的信息.
　　每一行有且仅有3个整数, 描述对应角色的初始位置, movement range, throwing range.
　　数据保证3个角色的初始位置两两不相同且所有的数字都在1到10之间.

输出格式

　　仅有1个整数, 即Laharl, Etna, Flonne之一能到达的最大距离.

样例输入

9 3 3
4 3 1
2 3 3

样例输出

15

样例说明

　　一开始Laharl在位置9, Etna在位置4, Flonne在位置2.
　　首先, Laharl移动到6.
　　然后Flonne移动到位置5并且举起Etna.
　　Laharl举起Flonne将其扔到位置9.
　　Flonne把Etna扔到位置12.
　　Etna移动到位置15.

题解：

题目已经提示了该题是搜索题。一开始也是没有思路的，搜索了网上的一些代码，虽然没有立刻看懂，但是了解到可能先弄懂全排列算法对解决该题会有帮助。的确如此，在解决了全排列问题后，再看这题就有思路了。具体可以看我上一篇的全排列整理。
理解全排列之后再看这题，就知道这题就是不断深搜和回溯的过程。
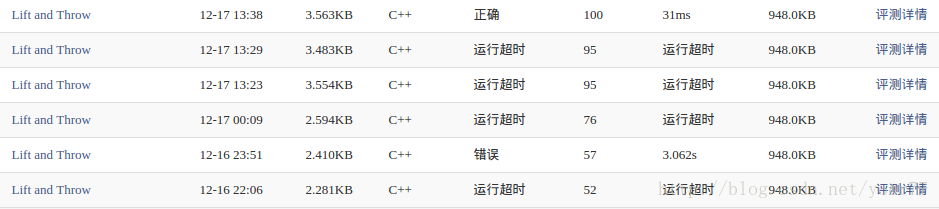
但是仅仅全排列肯定是超时的。这就需要细心地剪枝优化了。如下图，我第三次提交的时候76分，可以算出全部数据的正确结果，但是计算最大的数据需要10+s，妥妥的超时了。然后通过不断剪枝，不断发现可以优化的地方，从76分到95分，最后优化的代码计算最大的数据是需要31ms。可见剪枝对于搜索的重要性。

先来说说深搜的过程，然后再来说剪枝优化。

深搜：

一共有3个人，每个人有3种不同的动作，移动、举起旁边的人或扔出举起的人。所以加起来一共有9种不同的操作。
我们给这9中操作编码，分别为0~8，每次搜索都是从这8种不同的操作中选择一个操作进行下一次搜索。

搜索0，3，6时，即移动操作的时候，需要枚举他所能到达的所有地方。注意可以往前移动也可以往后移动。进行移动的人必须还没有进行过移动，因为每种操作只能进行一次，也不能是被举起或举起别人的状态。他所到达的地方必须是个空位置。

搜索1，4，7时，即举起别人的操作的时候，当前进行操作的人的状态不能是正在被举起，也不能是正在举起别人或者是已经进行过举起别人的操作。他能举起的只有和他距离相差为1的人。如果他旁边的人正在举起其他人，则他可以把这两个人一起举起来，要注意把最上面的人的位置也要修改一下。如果他旁边的人正在被别人举起，则不能重复举起这个人。

搜索2，5，8时，即抛的操作时，当前进行操作的人头顶必须有人，而且不能是正在被别人举起的状态。

剪枝：

首先，9个动作全排列，解答树不会超过9层。可以用一个step记录层数，用一个visit[]数组来记录每个操作是否执行过，下次深搜的时候只搜索那些9个操作中没有被执行过的操作。当前节点的搜索结束后visit[]数组要回溯。
第一次操作，只能是举起旁边的人或者移动，不可能是抛，因为头顶还没人。
最后一次操作，只能是往前走最远的距离或者向前抛最大的距离。举起操作不用考虑。

移动的时候，如果后面没有人，则肯定没有必要向后走。如果后面有人，也不需要从最大距离开始枚举，只需要从最后面的人的前面一个位置开始枚举就好了。当然移动的距离不能超过可以移动的最大距离。

抛也是如此，如果后面没有人，则没必要往后抛。也不需要从能往后抛的最大距离开始枚举，只需要从最后面的一个人的前一个位置开始枚举。抛的距离不能超过可以抛的最大距离。

我觉得移动的时候大多数位置是没有意义的，需要枚举的位置仅仅是其他人的旁边的位置或者能移动的最大距离这两种。

抛也是这样，只需要抛到其他人的旁边，或者抛到能向前抛的最大的距离。

下面是代码，加了满满的注释。throw的部分没什么注释，是因为感觉和move，lift部分的注释会有重复。
如果代码有问题请指正，欢迎讨论。

#include <iostream>
#include <cmath>
#include <cstring>
#define MAXLEN 50
using namespace std;

struct People
{
    int pos;
    bool lifted;//正在被举着
    bool lifting;//正在举着别人
    int lift;//举着的是谁
    int maxMove;//最大移动距离
    int maxThrow;//最大抛距离
    bool hasMoved;//是否移动过
    bool hasLifted;//是否举过别人
    //没有必要加上是否抛过别人的标记，因为只能举起别人一次
}p[3];
//数轴，标记当前位置上是否有人
bool Pos[MAXLEN]; 
//3个人每人3种动作，一共9中操作。全排列的话需要标记一下，一个排列中不能有重复操作
bool visit[10];
int Max = 0;//记录最大距离

/*
 * dfs 深搜查找可能的结果
 * @prarm k 表示当前是第n个人执行第m种操作。
 * 其中 n = k/3, m = k%3;
 * @prarm step 全排列中一共有9个元素，step指明当前操作排到了第几个元素。
 * @return void
 */
void dfs(int k, int step)
{

    int n = k / 3; //当前执行操作的人
    int m = k % 3; //当前执行的动作
    // move
    if(!m) {
        //如果此人正在被别人举着或者正在举着别人，或者已经移动过了，那么他/她不能移动。
        if(p[n].lifted || p[n].lifting || p[n].hasMoved) return;

        int i = 1;
        if(step == 9) i = p[n].maxMove;//如果当前是最后一步，那么直接向前移动可以移动的最远的距离
        //如果不是最后一步，那么他也不必从他能移动的最靠后的距离开始搜索
        //他只需要从 他的位置之前的 有人的位置 的前一个位置 开始搜索即可
        //如果他后面没人，那么他走的距离只需要从1开始搜索，不需要往后走，只需要往前走
        else {
            for(int j = 1; j < p[n].pos; j++) {
                if(Pos[j]) {
                    int l = -(p[n].pos - j -1);
                    i = l < i ? l : i;
                }
            }
            //走的距离不能超过maxMove
            i = i > -p[n].maxMove ? i : -p[n].maxMove;
        }
        for(; i <= p[n].maxMove; i++) {
            if(Pos[p[n].pos+i-1] || Pos[p[n].pos+i+1] || i == p[n].maxMove){
                if(p[n].pos + i > 0 && !Pos[p[n].pos + i]) {
                    if(!i) continue;

                    Pos[p[n].pos] = false;//当前位置置为false
                    p[n].pos += i;//向前走
                    Pos[p[n].pos] = true;//走到的新位置置为true
                    p[n].hasMoved = true;//标记一下，已经移动过了
                    Max = p[n].pos  > Max ? p[n].pos : Max;//记录最大距离

                    //继续搜索
                    for(int j = 0; j < 9; j++) {
                        if(!visit[j]) {
                            visit[j] = true;
                            dfs(j, step+1);
                            visit[j] = false;//回溯
                        }
                    }
                    //回溯
                    p[n].hasMoved = false;
                    Pos[p[n].pos] = false;
                    p[n].pos -= i;
                    Pos[p[n].pos] = true;
                }
            }
        }
    } 
    // lift
    else if(m == 1) {
        //如果当前这个人真在被举着或者真在举着别人，或者已经举起过别人了，那么他/她将不能再举起别人。
        if(p[n].lifted || p[n].lifting || p[n].hasLifted) return;
        for(int i = 0; i < 3; i++) {
            //如果旁边有人
            if(abs(p[i].pos-p[n].pos) == 1) {
                //如果旁边的这个人已经被别人举起了，则不能重复举起
                if(p[i].lifted) continue;

                p[n].hasLifted = true;
                p[n].lifting = true;
                p[n].lift = i;
                p[i].lifted = true;
                int temp = p[i].pos;
                Pos[p[i].pos] = false;
                p[i].pos = p[n].pos;
                //如果当前举起的人真在举着其他人，那么这两个人的位置必须同步改变
                if(p[i].lifting) {
                    int j = p[i].lift;
                    p[j].pos = p[i].pos;
                }

                //继续搜索
                for(int j = 0; j < 9; j++) {
                    if(!visit[j]) {
                        visit[j] = true;
                        dfs(j, step+1);
                        visit[j] = false;
                    }
                }
                //回溯
                p[n].hasLifted = false;
                p[n].lifting = false;
                p[n].lift = -1;
                p[i].lifted = false;
                p[i].pos = temp;
                Pos[p[i].pos] = true;
                if(p[i].lifting) {
                    int j = p[i].lift;
                    p[j].pos = p[i].pos;
                }
            }
        }
    }
    // throw
    else {
        //如果当前这个人正在被举起，或者他/她并没有举起别人，那么他/她不能执行抛的动作
        if(!p[n].lifting || p[n].lifted) return;

        int i = 1;
        if(step == 9) i = p[n].maxThrow;
        else {
            for(int j = 1; j < p[n].pos; j++) {
                if(Pos[j]) {
                    int l = -(p[n].pos - j -1);
                    i = l < i ? l : i;
                }
            }
            i = i > -p[n].maxThrow ? i : -p[n].maxThrow;
        }

        for(; i <= p[n].maxThrow; i++) {
            if(p[n].pos + i > 0 && !Pos[p[n].pos + i]) {
                if(Pos[p[n].pos+i-1] || Pos[p[n].pos+i+1] || i == p[n].maxThrow) {
                    int j = p[n].lift;
                    p[j].pos += i;
                    p[n].lifting  = false;
                    p[n].lift = -1;
                    p[j].lifted = false;
                    Pos[p[j].pos] = true;
                    Max = p[j].pos > Max ? p[j].pos : Max;
                    if(p[j].lifting) {
                        int k = p[j].lift;
                        p[k].pos = p[j].pos;
                    }
                    for(int q = 0; q < 9; q++) {
                        if(q == k) continue;
                        if(!visit[q]) {
                            visit[q] = true;
                            dfs(q, step+1);
                            visit[q] = false;
                        }
                    }
                    //回溯
                    Pos[p[j].pos] = false;
                    p[j].pos -= i;
                    p[j].lifted = true;
                    p[n].lift = j;
                    p[n].lifting = true;
                    if(p[j].lifting) {
                        int k = p[j].lift;
                        p[k].pos = p[j].pos;
                    }
                }
            }
        }
    }
}
int main()
{
    memset(Pos, false, sizeof(Pos));
    memset(visit, false, sizeof(visit));
    //输入
    for(int i = 0; i < 3; i++) {
        cin >> p[i].pos >> p[i].maxMove >> p[i].maxThrow;
        p[i].lifted = p[i].lifting = p[i].hasMoved = p[i].hasLifted = false;
        p[i].lift = -1;
        Pos[p[i].pos] = true;
    }
    //深搜
    for(int i = 0; i < 9; i++) {
        //一个合法的第一步，不可能是抛。必须先移动或者举起别人
        if((i % 3) != 2) 
        {
            visit[i] = true;
            dfs(i, 1);
            visit[i] = false;//回溯
        }
    }
    //结果
    cout << Max << endl;
    return 0;
}