普通线段树の基础

是什么

线段树是一种二叉搜索树，与区间树相似，它将一个区间划分成一些单元区间，每个单元区间对应线段树中的一个叶结点。使用线段树可以快速的查找区间和等，时间复杂度为O(logN)。而未优化的空间复杂度为O(2N)，实际应用时一般还要开4N的数组以免越界，因此有时需要离散化让空间压缩。（摘自度娘）

为什么要用

看一个问题——https://www.luogu.com.cn/problem/P3372

对于这道题目，我们如何处理？第一个想到的绝对是暴力修改，复杂度到达O（mn）的级别。然而，10^5的数据量告诉我们，显然这样会TLE。乍一看，刚学树状数组的童鞋也许会跃跃欲试，然而，纯树状数组一般只支持区间查询和单点修改，要修改一个区间只能循环一个一个暴力修改，那一次修改就占到mlogn的离谱时间复杂度，肯定也是被卡的份。咋办？线段树就能很好解决此问题。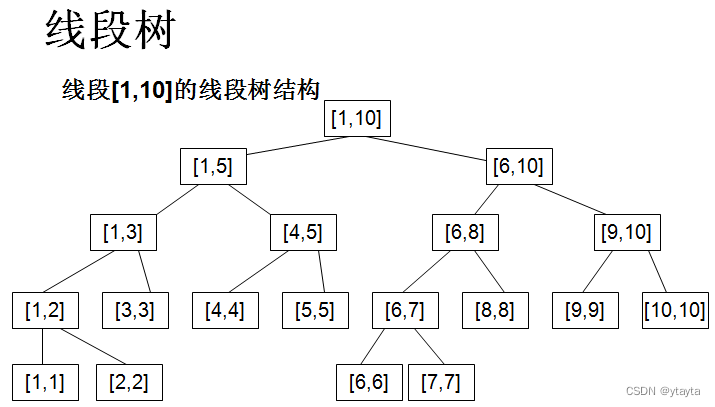

以上为线段树每个节点之间的关系以及它们维护的区间

怎么用

建树

因为线段树是一棵平衡二叉树，我们完全可以以数组的方式直接存树。假如数组为tr[]，那tr[p]的左儿子就是tr[p*2]，右儿子是tr[p*2+1]。对于每一个节点，它都对应维护着一个区间，一般来说，假如有n个元素编号从1到n，tr[1]维护的便是[1,n]区间和，其左儿子维护[1,n/2],右儿子维护[n/2+1,n]，此后在递归左右儿子的同时依次二分，直到分至维护的区间内只有一个元素，一个元素的区间和，那就十分简单了，在那以后，在递归回溯的过程中，将左右儿子维护的区间和依次相加，得到自己的区间和（就是通常所说的push_up操作），便完成了线段树的建树操作

#include<bits/stdc++.h>
#define int long long
using namespace std;
int tree[400000],sign[400000];
void build(int rand1,int rand2,int p){
	if(rand1==rand2){
		scanf("%lld",tree+p);
		return;
	}
	int m=1ll*(rand1+rand2)>>1;
	build(rand1,m,p<<1);
	build(m+1,rand2,p<<1|1);
	tree[p]=tree[p<<1]+tree[p<<1|1];
}

单点修改

这里体现了线段树的又一个便利性。找到需要修改的单点，将其修改，回溯后将与这个元素有关的区间和全部更新即可。

void update_point(int rand1,int rand2,int p,int aim,int k){
    if(rand1==rand2){
        tr[p]+=k;
        return;
    }
    int m=rand1+rand2>>1;
    if(m>=aim) update_point(rand1,m,p<<1,aim,k);
    else update_point(m+1,rand2,p<<1|1,aim,k);
}

区间查询

若要查询一段区间和，需要做的也不难。如果左右儿子维护的区间与待查询区间存在交集，那么就递归下去，直到当前节点维护的区间包含于待查询区间，然后直接返回该区间的值。可以证明，以此方法便可以获得待查询区间的完整区间和

int find(int rand1,int rand2,int p,int start,int end){
	if(rand1>=start && rand2<=end){
		return tree[p];
	}
	int m=1ll*(rand1+rand2)>>1,sum=0;
	if(m>=start) sum+=find(rand1,m,p<<1,start,end);
	if(m<end) sum+=find(m+1,rand2,p<<1|1,start,end);
	return sum;
}

到此为止，线段树的功能树状数组大多也能实现，接下来就是线段树所特有的东西喽

区间修改

若要对一个完整的区间进行修改，就如整体加上一个值，当然可以用单点修改的方式暴力一个个改(那样的话，线段树和树状数组功能有毛区别，这样的方式显然达不到所需效率）可以注意到，我们修改的所有元素以及包含它们的所有区间节点，并不一定在区间查询时会查到，这就代表着老老实实把所有区间改完是完全没有必要的。因此，此处引入一个提升线段树效率的关键所在——懒标记，有了它，我们就可以直接给整个区间。对于待修改区间，我们在直接修改这个区间的值的同时，打上一个懒标记，记录代表该区间的节点的所有子树都要进行如此修改即可。然而，这就意味着每次对树的遍历，都应该关注该节点的标记，将懒标记的信息下放到它的左右儿子，而做此事的就是push_down函数

​
void push_down(int rand1,int rand2,int p){
	if(sign[p]){
		int m=1ll*(rand1+rand2)>>1;
		sign[p<<1]+=sign[p];
		sign[p<<1|1]+=sign[p];
		tree[p<<1]+=1ll*(m-rand1+1)*sign[p];
		tree[p<<1|1]+=1ll*(rand2-m)*sign[p];
		sign[p]=0;
	}
}
void update_range(int rand1,int rand2,int p,int aim1,int aim2,int add){
	if(aim1<=rand1 && aim2>=rand2){
		sign[p]+=add;
		tree[p]+=(rand2-rand1+1)*add;
		return;
	}
	push_down(rand1,rand2,p);
	int m=1ll*(rand1+rand2)>>1;
	if(m>=aim1) update_range(rand1,m,p<<1,aim1,aim2,add);
	if(m<aim2) update_range(m+1,rand2,p<<1|1,aim1,aim2,add);
	tree[p]=tree[p<<1]+tree[p<<1|1];
}

​

此外，如果区间修改存在，线段树代码中除建树、push_down本身以外其余的都要在递归左右儿子前加上push_down函数，以便遍历时左右儿子能够正常更新。

接下来贴模板完整代码——

#include<bits/stdc++.h>
#define int long long
using namespace std;
int tree[400000],sign[400000];
void build(int rand1,int rand2,int p){
	if(rand1==rand2){
		scanf("%lld",tree+p);
		return;
	}
	int m=1ll*(rand1+rand2)>>1;
	build(rand1,m,p<<1);
	build(m+1,rand2,p<<1|1);
	tree[p]=tree[p<<1]+tree[p<<1|1];
}
void push_down(int rand1,int rand2,int p){
	if(sign[p]){
		int m=1ll*(rand1+rand2)>>1;
		sign[p<<1]+=sign[p];
		sign[p<<1|1]+=sign[p];
		tree[p<<1]+=1ll*(m-rand1+1)*sign[p];
		tree[p<<1|1]+=1ll*(rand2-m)*sign[p];
		sign[p]=0;
	}
}
void update_range(int rand1,int rand2,int p,int aim1,int aim2,int add){
	if(aim1<=rand1 && aim2>=rand2){
		sign[p]+=add;
		tree[p]+=(rand2-rand1+1)*add;
		return;
	}
	push_down(rand1,rand2,p);
	int m=1ll*(rand1+rand2)>>1;
	if(m>=aim1) update_range(rand1,m,p<<1,aim1,aim2,add);
	if(m<aim2) update_range(m+1,rand2,p<<1|1,aim1,aim2,add);
	tree[p]=tree[p<<1]+tree[p<<1|1];
}
int find(int rand1,int rand2,int p,int start,int end){
	if(rand1>=start && rand2<=end){
		return tree[p];
	}
	push_down(rand1,rand2,p);
	int m=1ll*(rand1+rand2)>>1,sum=0;
	if(m>=start) sum+=find(rand1,m,p<<1,start,end);
	if(m<end) sum+=find(m+1,rand2,p<<1|1,start,end);
	return sum;
}
signed main()
{
	signed n,q,k,a,b,x;
	scanf("%d%d",&n,&q);
	build(1,n,1);
	for(int i=0;i<q;i++){
		scanf("%d%d%d",&k,&a,&b);
		if(k==1){
			scanf("%d",&x);
			update_range(1,n,1,a,b,x);
		}else{
			printf("%lld\n",find(1,n,1,a,b));
		}
	}
	return 0;
}

可见线段树的码量相比树状数组有“亿点点”长，这就是为啥虽然“可以用树状数组的一定能用线段树做”，但“如果能用树状数组就不用线段树”。（而且树状数组实际上可以比线段树快一丢丢）

下面章节小白回避

接下来是一道不错的线段树略微进阶题，就这损玩意——https://www.luogu.com.cn/problem/P2572

码字前想的东西

显然，线段树能够维护的信息远不止区间和一种。这里，我们需要求最长的连续1，为了在向上回溯的时候有效维护此信息，这就要求我们维护3个信息——

am->代表该区间连续1的最长长度；

lm->代表该区间从最左边开始往右连续的1的长度；

rm->代表该区间从最右边开始往左连续的1的长度。

然而，注意到取反这一个操作，这就代表着0/1只是相对的，换句话说，这段区间中从前的0也许在取反操作后就是现在的1。这样，为了有效应对取反，上述的信息对于0/1就都需要维护

其实，线段树本身也可以用结构体封装，尤其当维护的量比较多时，结构体写起来个人认为比较顺手。代码与封装前差不多

#include<bits/stdc++.h>
#define len(p) tr[p].r-tr[p].l+1
using namespace std;
const int N=100010;
inline int read()
{
 	int f = 1,x = 0; char ch = getchar();
	while(ch > '9' || ch < '0'){if(ch == '-')f = -1; ch = getchar();}
	while(ch >= '0' && ch <= '9'){x=(x << 1)+(x << 3)+(ch ^ 48); ch = getchar();}
	return f*x;
}
inline void write(int x)
{
 	if(x < 0){putchar('-'); x = -x;}
	if(x > 9)write(x / 10); putchar((x % 10) ^ 48);
	return;
}
struct tree{
	int l,r;
	int sum,lm[2],rm[2],am[2];
	short sign;//0 无；1 全部变成1；2 全部变成0；3 全部取反 
}tr[N<<2];
void build(int rand1,int rand2,int p){
	tr[p].l=rand1,tr[p].r=rand2;//注意结构体封装可以也把区间左右端的值提前存起来
	if(rand1==rand2){
		tr[p].sum=tr[p].am[1]=tr[p].lm[1]=tr[p].rm[1]=read();
		tr[p].am[0]=tr[p].lm[0]=tr[p].rm[0]=tr[p].sum^1;
		return;
	}
	int m=tr[p].l+tr[p].r>>1;
	build(rand1,m,p<<1);build(m+1,rand2,p<<1|1);
	push_up(p);//马上讲回溯时该怎么做
}

push_up怎么写

这道题的难点之一就是push_up怎么写，在建树过程中，向上回溯时对区间进行的维护是极为讲究的，这也便是维护am,rm,lm的最关键意义。

对于一个节点而言，其am其实就是左右儿子的am与左儿子的rm+右儿子的lm（因为有可能最长连续1/0横贯了左右儿子区间）的最大值，而rm的值，需分类讨论：若右儿子内全是1/0，rm就可以横贯并越至左儿子的rm，否则就只能继承右儿子的rm。lm也是类似的道理。

inline void push_up(int p){
	tr[p].sum=tr[p<<1].sum+tr[p<<1|1].sum;
	tr[p].am[0]=max(tr[p<<1].rm[0]+tr[p<<1|1].lm[0],max(tr[p<<1].am[0],tr[p<<1|1].am[0]));
	tr[p].am[1]=max(tr[p<<1].rm[1]+tr[p<<1|1].lm[1],max(tr[p<<1].am[1],tr[p<<1|1].am[1]));
	if(!tr[p<<1].sum/*全0*/) tr[p].lm[0]=len(p<<1)+tr[p<<1|1].lm[0];
	else tr[p].lm[0]=tr[p<<1].lm[0];
	if(tr[p<<1].sum==len(p<<1)/*全1*/) tr[p].lm[1]=len(p<<1)+tr[p<<1|1].lm[1];
	else tr[p].lm[1]=tr[p<<1].lm[1];
	if(!tr[p<<1|1].sum) tr[p].rm[0]=len(p<<1|1)+tr[p<<1].rm[0];
	else tr[p].rm[0]=tr[p<<1|1].rm[0];
	if(tr[p<<1|1].sum==len(p<<1|1)) tr[p].rm[1]=len(p<<1|1)+tr[p<<1].rm[1];
	else tr[p].rm[1]=tr[p<<1|1].rm[1];
}

下面，建树、区间修改、区间和查询都十分基础，便不一一赘述。

下放push_down

接下来，就是树的push_down环节。这里又是这道题的难点之一：因为取反操作的特殊性，它不能直接覆盖掉先前的懒标记，而相当于对先前懒标记的“取反”->若先前需全部赋1，这里就改成全赋0，反正亦然，只有当当前子节点啥也不是时才可以直接传递下去

inline void push_down(int p){
	if(tr[p].sign){
		if(tr[p].sign==3){
			if(tr[p<<1].sign==3) tr[p<<1].sign=0;
			else if(tr[p<<1].sign==2) tr[p<<1].sign=1;
			else if(tr[p<<1].sign==1) tr[p<<1].sign=2;
			else tr[p<<1].sign=3;
		}else tr[p<<1].sign=tr[p].sign;
		if(tr[p].sign==3){
			if(tr[p<<1|1].sign==3) tr[p<<1|1].sign=0;
			else if(tr[p<<1|1].sign==2) tr[p<<1|1].sign=1;
			else if(tr[p<<1|1].sign==1) tr[p<<1|1].sign=2;
			else tr[p<<1|1].sign=3;
		}else tr[p<<1|1].sign=tr[p].sign;
		switch(tr[p].sign){
			case 1:
				tr[p<<1].am[0]=tr[p<<1].lm[0]=tr[p<<1].rm[0]=0;
				tr[p<<1|1].am[0]=tr[p<<1|1].lm[0]=tr[p<<1|1].rm[0]=0;
				tr[p<<1].am[1]=tr[p<<1].lm[1]=tr[p<<1].rm[1]=len(p<<1);
				tr[p<<1|1].am[1]=tr[p<<1|1].lm[1]=tr[p<<1|1].rm[1]=len(p<<1|1);
				tr[p<<1].sum=len(p<<1),tr[p<<1|1].sum=len(p<<1|1);
				break;
			case 2:
				tr[p<<1].am[1]=tr[p<<1].lm[1]=tr[p<<1].rm[1]=0;
				tr[p<<1|1].am[1]=tr[p<<1|1].lm[1]=tr[p<<1|1].rm[1]=0;
				tr[p<<1].am[0]=tr[p<<1].lm[0]=tr[p<<1].rm[0]=len(p<<1);
				tr[p<<1|1].am[0]=tr[p<<1|1].lm[0]=tr[p<<1|1].rm[0]=len(p<<1|1);
				tr[p<<1].sum=tr[p<<1|1].sum=0;
				break;
			case 3:
				swap(tr[p<<1].am[0],tr[p<<1].am[1]);
				swap(tr[p<<1].rm[0],tr[p<<1].rm[1]);
				swap(tr[p<<1].lm[0],tr[p<<1].lm[1]);
				tr[p<<1].sum=len(p<<1)-tr[p<<1].sum;
				swap(tr[p<<1|1].am[0],tr[p<<1|1].am[1]);
				swap(tr[p<<1|1].rm[0],tr[p<<1|1].rm[1]);
				swap(tr[p<<1|1].lm[0],tr[p<<1|1].lm[1]);
				tr[p<<1|1].sum=len(p<<1|1)-tr[p<<1|1].sum;
				break;
		}
		tr[p].sign=0;
	}
}

区间找连续

最后来到了这题一个十分奇葩的地方——查找区间连续1，这也许是这道题最后一个难点。我们注意到，线段树维护的有关信息是“隔断”的，说白了这个区间维护的所有信息只与当前区间有关，但查找连续的1显然就是一个查找“连续量”的过程，往往待查找的区间又是横贯多个节点所代表的区间的。因此，仿照我们向上回溯过程做的事情，我们访问的绝不仅仅是当前区间的am那么简单，rm，lm一样也不能少，甚至判断数据是否装满代表sum都要访问。这里于是我把查找函数本身就定义为一个“线段树节点”一样的东西，便于返回值时把这些变量统统返回去。（这样写函数我也是第一次，手感奇奇怪怪）实际递归查找时分3种情况：

1.待查找区间全在左儿子，直接递归左儿子

2.待查找区间全在右儿子，直接递归右儿子

3.横贯左右儿子的区间，在分别递归查找左右儿子区间与待查找区间交集所代表的所有线段树的量后仿照向上回溯时的做法，将这区间所有相关量全部获取到即可

tree find_con(int p,int aim1,int aim2){
	//cout<<tr[p].l<<' '<<tr[p].r<<endl;
	if(aim1==tr[p].l && aim2==tr[p].r) return tr[p];
	push_down(p);
	int m=tr[p].l+tr[p].r>>1;
	if(m<aim1) return find_con(p<<1|1,aim1,aim2);
	else if(m>=aim2) return find_con(p<<1,aim1,aim2);
	else{
		tree t1=find_con(p<<1,aim1,m),t2=find_con(p<<1|1,m+1,aim2),t3;
		t3.sum=t1.sum+t2.sum;
		for(short i=0;i<=1;i++){
			t3.lm[i]=t1.lm[i];
			if(i && t1.sum==t1.r-t1.l+1) t3.lm[i]+=t2.lm[i];
			else if(!i && !t1.sum) t3.lm[i]+=t2.lm[i];
			t3.rm[i]=t2.rm[i];
			if(i && t2.sum==t2.r-t2.l+1) t3.rm[i]+=t1.rm[i];
			else if(!i && !t2.sum) t3.rm[i]+=t1.rm[i];
			t3.am[i]=t1.rm[i]+t2.lm[i];
			t3.am[i]=max(t3.am[i],max(t1.am[i],t2.am[i]));
		}
		return t3;
	}
}

可见这题码量非常的友好。完整代码不高兴贴了，自己写去吧。

线段树の注意事项

1.搞清楚这道题到底要维护区间的哪几个信息，尤其是懒标记的种类。想好再写

2.一个准确无误的push_down是线段树成功的一半，关注好懒标记之间的关系，这里可以边捋边打。线段树出错，80%都是在push_down这一环，因此这个函数值得好好检查

3.线段树区间长度是r-l+1，当出现奇奇怪怪的错误（尤其是当区间所有数均为正时莫名其妙出现负数），大概率是把区间长度打成l-r+1了

4.在区间修改当中如果+*共存，又有取模运算，最好先执行乘法再执行加法。就比如：http://luogu.com.cn/problem/P3373。这项注意点扩展开来就是要考虑严格考虑精度问题（开long long也是一个解决办法，就是慢了点），另外，取模多一点总比少好，有时WA就是因为取模不够勤快

7.23 Update:动态开点线段树

Ps:为体现动态开点线段树的优势，本章节内容将结合树链剖分进行讲解，若树剖0基础或基础不扎实请移步树链剖分进行学习。

大家先看一道例题：https://www.luogu.com.cn/problem/P3313，翻译成人话就是讲：在一棵树上，每个节点有俩权值，现在相当于给你目标2号权值（就是所谓的“信仰”）已知起点、终点，问最短路径上每个2号权值等于目标权值的节点，其1号权值（就是所谓的“评级”）的最大值以及和，中间还伴随着节点上俩权值的单点修改。相信聪明的你很容易就明白了这是一道用树剖解决的模板题，然而，常规的树剖是不在乎什么2号权值的，只是将所及之处所有节点的点权暴力相加，也许你会大声疾呼：为每一个2号权值专门建一棵树，对于维护2号权值i的线段树，将原树上2号权值不是i的点对应到线段树上值统统赋0，其余不变。然而这种朴(bao)素(li)想法有一个最大问题：本题2号权值种数到达了10^5级别，也就是说开的总节点数达到了惊人的4e10级别，这样的大小，别说int了，bitset也经不起这么开。因此，动态开点的线段树便应运而生。

基本信息

梗概：动态开点的线段树是专门针对线段树巨大空间复杂度而改良的线段树变种。它不再依赖于堆式存储方式（就是tr[p]左儿子tr[p*2]右儿子tr[p*2+1]那玩意），而是采用动态开点，每多出一个新节点就分配一个，因此没有浪费，而此时，tr[p*2]，tr[p*2+1]已经不再代表左右俩儿子了，这里一般用2个变量lc rc记录父节点左右儿子的下标（其实用指针记录可能相对略快，差不多意思，但我不敢用）。

适用范围：尤其适用于所需线段树数量较多而常规线段树无法存储的情况，少数维护区间大到离谱的题目也许也能用。这种线段树也是为后续学习主席树打下了基础。

空间复杂度：一般是O(nlogn)。因为线段树是一个完全二叉树，每一次最多遍历logn+1个节点。实际开数组还是推荐不MLE前提下尽量开大些

具体操作

建树

啥？建树？没搞错吧，你用动态开点的目的是啥还记得不？说白了不就是每一个维护2号权值的线段树针对每一个2号权值与自身维护的那个不一样的点没有给它腾空间的必要吗。如果像常规线段树那样建一棵完整的树，那么每一个线段树又要占4N个节点，图啥？

更新节点

讲讲动态开点线段树的工作原理。就拿区间为[1,10]的一棵树举例

就比如一开始给它添加节点[2,2]，权值为5

 

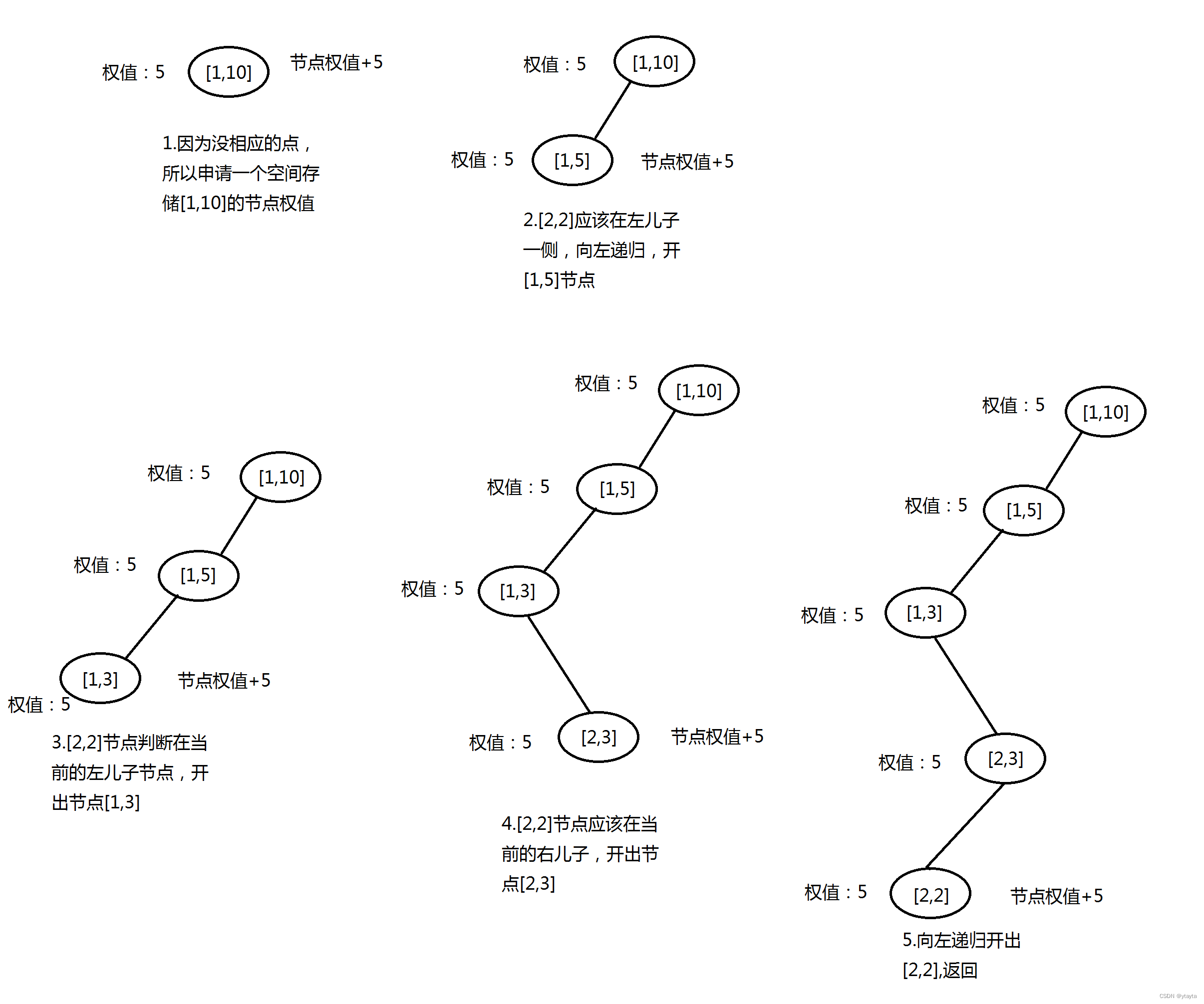
 总的来说，其实就几点：访问单点所在区间，如果没有就自己开一个，一直到访问到达目标节点为止。需要注意的是：与常规线段树不同，这里采用了下探同时预处理节点的方式而非在递归回溯时开始处理

代码：

void update(int &p,int rand1,int rand2,int val,int pos){
	if(!p) p=++tot;
	tr[p].maxn=max(tr[p].maxn,val),tr[p].sum+=val;
	if(rand1==rand2) return;
	int mid=rand1+rand2>>1;
	if(mid>=pos) update(tr[p].lc,rand1,mid,val,pos);
	else update(tr[p].rc,mid+1,rand2,val,pos);
}

删除节点

我们再来看看上面的例题，对于“CC”操作，其实就相当于把维护一个2号权值的线段树的一个节点值“搬运”到另一个上面，对于“CW”操作，其实就是先把原位置的节点删除后再给它一个新值。二者都离不开一个操作：删除。所谓删除，其实就是吧这一个叶节点的所有值都变为初始值（通常是0），这样看来，代码其实不难理解

void dele(int &p,int rand1,int rand2,int pos){
	if(rand1==rand2){
		tr[p].maxn=tr[p].sum=0;
		return;
	}
	int mid=rand1+rand2>>1;
	if(mid>=pos) dele(tr[p].lc,rand1,mid,pos);
	else dele(tr[p].rc,mid+1,rand2,pos);
	tr[p].sum=tr[tr[p].lc].sum+tr[tr[p].rc].sum;
	tr[p].maxn=max(tr[tr[p].lc].maxn,tr[tr[p].rc].maxn);
}

查询

与常规线段树大同小异

int find_sum(int p,int rand1,int rand2,int aim1,int aim2){
	if(rand1>=aim1 && rand2<=aim2) return tr[p].sum;
	int mid=rand1+rand2>>1,sum=0;
	if(mid>=aim1) sum+=find_sum(tr[p].lc,rand1,mid,aim1,aim2);
	if(mid<aim2) sum+=find_sum(tr[p].rc,mid+1,rand2,aim1,aim2);
	return sum;
}
int find_max(int p,int rand1,int rand2,int aim1,int aim2){
	if(rand1>=aim1 && rand2<=aim2) return tr[p].maxn;
	int mid=rand1+rand2>>1,maxn=INT_MIN;
	if(mid>=aim1) maxn=max(maxn,find_max(tr[p].lc,rand1,mid,aim1,aim2));
	if(mid<aim2) maxn=max(maxn,find_max(tr[p].rc,mid+1,rand2,aim1,aim2));
	return maxn;
}

代码

以上就是本例题所要用到的动态开点线段树的所有操作，接下来贴完整代码

#include<bits/stdc++.h>
using namespace std;
inline int read()
{
	int f = 1,x = 0; char ch = getchar();
	while(ch > '9' || ch < '0'){if(ch == '-')f = -1; ch = getchar();}
	while(ch >= '0' && ch <= '9'){x=(x << 1)+(x << 3)+(ch ^ 48); ch = getchar();}
	return f*x;
}
inline void write(int x)
{
	if(x < 0){putchar('-'); x = -x;}
	if(x > 9)write(x / 10); putchar((x % 10) ^ 48);
	return;
}
const int N=1e5+5;
int w[N],c[N];
struct ed{
	int to,nex;
}e[N<<1];
int head[N],cnt;//链式前向星存图
int fa[N],dep[N],siz[N],hson[N];
void dfs1(int u){
	siz[u]=1;
	for(int i=head[u];i;i=e[i].nex){
		int v=e[i].to;
		if(fa[u]==v) continue;
		dep[v]=dep[u]+1,fa[v]=u;
		dfs1(v);
		siz[u]+=siz[v];
		if(!hson[u] || siz[v]>siz[hson[u]]) hson[u]=v;
	}
}
int top[N],rev[N],id[N],tot;
void dfs2(int u,int t){
	top[u]=t,id[u]=++tot,rev[tot]=u;
	if(!hson[u]) return;
	dfs2(hson[u],t);
	for(int i=head[u];i;i=e[i].nex){
		int v=e[i].to;
		if(fa[u]==v || v==hson[u]) continue;
		dfs2(v,v);
	}
}//常规树剖
struct stree{
	int lc,rc;
	int sum,maxn;
}tr[N*20];
int root[N],q,n;//root[i]：表示维护2号权值i的线段树的根节点为root[i]
inline int max(int a,int b){
	return a>b?a:b;
}
inline void swap(int &a,int &b){
	a^=b^=a^=b;
}//手打函数，貌似比系统内直接调用的快？
void update(int &p/*取值符：在函数内变量值变化时被引用的变量值也会变化*/,int rand1,int rand2,int val,int pos){
	if(!p) p=++tot;
	tr[p].maxn=max(tr[p].maxn,val),tr[p].sum+=val;
	if(rand1==rand2) return;
	int mid=rand1+rand2>>1;
	if(mid>=pos) update(tr[p].lc,rand1,mid,val,pos);
	else update(tr[p].rc,mid+1,rand2,val,pos);
}
void dele(int &p,int rand1,int rand2,int pos){
	if(rand1==rand2){
		tr[p].maxn=tr[p].sum=0;
		return;
	}
	int mid=rand1+rand2>>1;
	if(mid>=pos) dele(tr[p].lc,rand1,mid,pos);
	else dele(tr[p].rc,mid+1,rand2,pos);
	tr[p].sum=tr[tr[p].lc].sum+tr[tr[p].rc].sum;
	tr[p].maxn=max(tr[tr[p].lc].maxn,tr[tr[p].rc].maxn);
}
int find_sum(int p,int rand1,int rand2,int aim1,int aim2){
	if(rand1>=aim1 && rand2<=aim2) return tr[p].sum;
	int mid=rand1+rand2>>1,sum=0;
	if(mid>=aim1) sum+=find_sum(tr[p].lc,rand1,mid,aim1,aim2);
	if(mid<aim2) sum+=find_sum(tr[p].rc,mid+1,rand2,aim1,aim2);
	return sum;
}
int find_max(int p,int rand1,int rand2,int aim1,int aim2){
	if(rand1>=aim1 && rand2<=aim2) return tr[p].maxn;
	int mid=rand1+rand2>>1,maxn=INT_MIN;
	if(mid>=aim1) maxn=max(maxn,find_max(tr[p].lc,rand1,mid,aim1,aim2));
	if(mid<aim2) maxn=max(maxn,find_max(tr[p].rc,mid+1,rand2,aim1,aim2));
	return maxn;
}
int qsum(int u,int v,int belie){
	int ans=0;
	while(top[u]!=top[v]){
		if(dep[top[u]]<dep[top[v]]) swap(u,v);
		ans+=find_sum(root[belie],1,n,id[top[u]],id[u]);
		u=fa[top[u]];
	}
	if(dep[u]<dep[v]) swap(u,v);
	ans+=find_sum(root[belie],1,n,id[v],id[u]);
	return ans;
}
int qmax(int u,int v,int belie){
	int ans=INT_MIN;
	while(top[u]!=top[v]){
		if(dep[top[u]]<dep[top[v]]) swap(u,v);
		ans=max(ans,find_max(root[belie],1,n,id[top[u]],id[u]));
		u=fa[top[u]];
	}
	if(dep[u]<dep[v]) swap(u,v);
	ans=max(ans,find_max(root[belie],1,n,id[v],id[u]));
	return ans;
}
int main()
{
	n=read(),q=read();
	char opt[4];int a,b;
	for(int i=1;i<=n;i++) w[i]=read(),c[i]=read();
	for(int i=1;i<n;i++){
		a=read(),b=read();
		e[++cnt].to=a,e[cnt].nex=head[b],head[b]=cnt;
		e[++cnt].to=b,e[cnt].nex=head[a],head[a]=cnt;
	}
	dfs1(1);dfs2(1,1);tot=0;
	for(int i=1;i<=n;i++)
		update(root[c[i]],1,n,w[i],id[i]);
	while(q--){
		scanf("%s",opt);a=read(),b=read();
		switch(opt[1]){
			case 'C':
				dele(root[c[a]],1,n,id[a]);
				update(root[b],1,n,w[a],id[a]);
				c[a]=b;
				break;
			case 'W':
				dele(root[c[a]],1,n,id[a]);
				update(root[c[a]],1,n,b,id[a]);
				w[a]=b;
				break;
			case 'S':
				write(qsum(a,b,c[a]));
				puts("");
				break;
			case 'M':
				write(qmax(a,b,c[a]));
				puts("");
				break;
		}
	}
	return 0;
}

持续更新中……