漫画统计学整理

本文文献来自《漫画学统计》，PDF版下载链接
本文参考：《漫画统计学》读书笔记
本文思维导图：《漫画统计学》思维导图

一、数据种类

数据分为 “不可测量”的数据 和 “可测量” 的数据

二、掌握数据整体的状态（数值数据）

5、分布表的组距、分组定义（单独讲解）

例如：对以下数据 价格在500-980区间范围内（共50条）的数据进行分组和确定组距

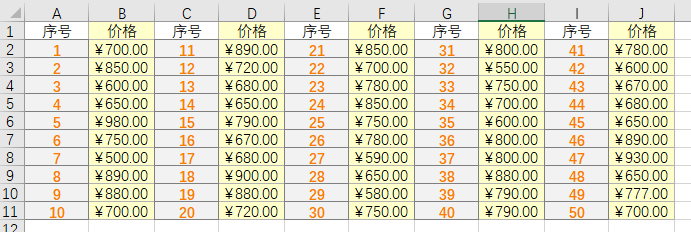
①通常出于数据习惯进行分组和定义组距

将整体看成500-1000的区间，再按照100的组距来分组，共分5组（即500-600，600-700…，900-1000），每组间距为100。如下图进行设置表格：

②采用史特吉斯公式确定分组和组距

得到分组结果为：7 、得到组距结果为：69

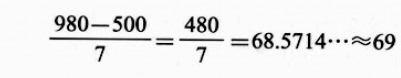
最后根据得到的分组、组距设置如下表格：

补充：推断统计学和描述统计学

（1）推断统计学：从样本的信息推测整体状况；
（2）描述统计学：借由整理资料，尽可能简单明了地显示出整体状况为目的的统计学，即将对象集合视为一个总体的统计学；

三、标准计分和离差

关于标准计分和离差的举例

四、求机率

2、正太分布（单独讲解）

特征：（1）以平均值为中心呈左右对称、（2）受到平均值和标准差的影响

统计学中，将x的机率密度函数符合上述公式的，以“x服从平均值为OO，标准值为XX的正态分布”来表示

3、标准正太分布（单独讲解）

将初始数据进行标准化（计算出每条数据的标准计分，标准计分=[(每一数据)-(平均数)] / 标准差）

标准化后的标准计分的平均数势必为0、而其标准差势必为1【第三章提到】，因此得到后的就是 “标准正太分布”


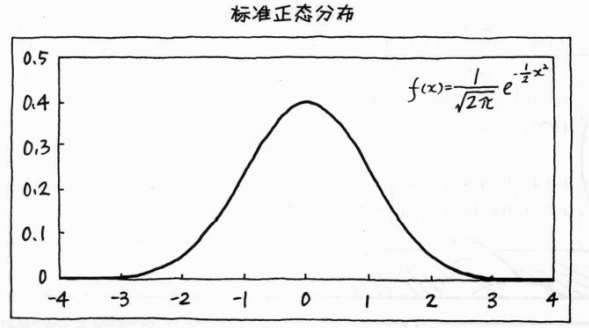
可通过标准正太分布表来求出某个值在正太分布图中的 “ 面积 / 比例 / 机率 ” 可查看该举例链接

4、卡方分布（单独讲解）

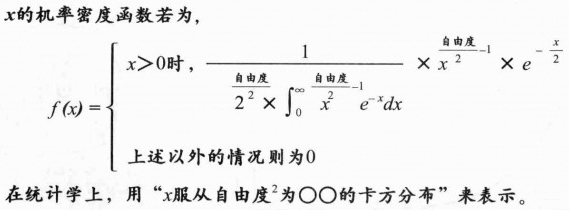
非数学家不必对该公式进行深究。
只需关注其中的 '自由度' 即可，自由度，类似 f(x) = ax + b 中的斜率 a，会影响图像形状的数值
所以只要自由度的值有所改变，图形的形状也会随之改变

卡方分布表：记录了对应这个部分的机率（=面积=比例）P的横轴刻度 x²（即卡方）之值的表；类似于正态分布表；

“标准正态分布表” 为记录对应横轴的刻度之机率的表； “卡方分布表” 则记录对应机率之横轴刻度的表；

可自行在卡方分布表中查出对应的卡方值，详细可查看举例链接

5、t分布（单独讲解）

6、F分布（单独讲解）

7、“XX分布” 和 EXCEL（单独讲解）

分布	函数	函数的特征
正态分布	NOPMDIST	可计算对应横轴刻度的机率
正态分布	NOPMINV	可计算对应机率的横轴刻度
标准正态分布	NOPMDIST	可计算对应横轴刻度的机率
标准正态分布	NOPMINV	可计算对应机率的横轴刻度
卡方分布	CHIDIST	可计算对应横轴刻度的机率
卡方分布	CHINV	可计算对应机率的横轴刻度
t分布	TDIST	可计算对应横轴刻度的机率
t分布	TINV	可计算对应机率的横轴刻度
F分布	FDIST	可计算对应横轴刻度的机率
F分布	FINY	可计算对应机率的横轴刻度

由于正态分布的机率密度函数受到平均值和标准差的影响。因此即使想做出“正太分布表”也是不可能的。然而，利用EXCEL来求出与“正太分布表”相当的值却非常便利。

五、双变量的相关分析

1、相关系数（单独讲解）

正相关、负相关和不相关👇 ------------ 关于相关系数的举例可查看该链接

2、相关比（单独讲解）

相关比值的范围介于0~1之间；两个变量的关联性越强，则相关比的值就会越接近1；越弱，越接近0
关于相关比的举例可查看该链接

1. 相关比的值为1，则各组所含数据相同，组内变异为0；
2. 相关比的值为0，则各组的平均值相同，组间变异为0；
   

3、克莱姆相关系数（单独讲解）

“克莱姆相关系数” 也可称为 “克莱姆得关联系数”、“克莱姆V” 或 “独立系数”

关于 观测次数 和 期望次数，以及克莱姆相关系数的算法，可参考该链接

若观测次数和期望次数的差异越大，则分类数据之间的关联程度越强，且皮尔森的卡方统计量 $x_0^2$ 也会越大

总结

• 相关系数为表示数值数据和数值数据的关联程度的指标；
• 相关比为表示数值数据和分类数据的关联程度的指标；
• 克莱姆相关系数为表示分类数据和分类数据的相关程度的指标；
• 相关系数、相关比和克莱姆相关系数中，在统计学上，并无 “其值若在xx以上时，则两变量的关联性较强” 的标准
• 相关系数、相关比和克莱姆相关系数的特征如下表所示：

	最小值	最大值	两变量完全不相关时的值	两变量相关性最强时的值
相关系数	-1	1	0	-1或1
相关比	0	1	0	1
克莱姆相关系数	0	1	0	1

六、深入理解独立性检验

1、检验（单独讲解）

检验有许多种类，如：
独立性检验、相关比检验、无相关检验、总体平均数差检验、总体比例差检验等；检验的种类虽然多样，但步骤都是一样的

2、独立性检验（单独讲解）

所谓 独立性检验 指的是：推测 “总体的克莱姆相关系数的值是否为0” 的分析方法；
换句话说，就是推测 “交叉资料表中的两变量是否相关” 的分析方法，也称为 “卡方检验”；
详细见该链接（讲解+例题）

当 总体的克莱姆相关系数=0，则 “皮尔森卡方统计量 $x_0^2$ ” 遵守自由度为2的卡方分布 ，如下图所示：

（1）主体：总体是由分析者决定。比如设定“居住在都市的有选举权者”和“居住在农村的有选举权者”为总体，那么，“都市”具体指哪里呢，是“东京都”还是“各都道府县的地方政府所在地”，这是由分析者决定的；

（2）虚无假说和对立假说见下节；

（3）检验种类：分析者决定，选择符合分析目的的检验。独立性检验 / 相关比检验 / 无相关检验等五个；

（4）置信水平：分析者决定置信水平。置信水平一般设为 0.05 或 0.01 ，通常以 α 符号表示；

（5）求出检验统计量的值：检验统计量是指将样本资料转换为1个值的公式。检验种类不同，检验统计量也会不同。
若是 独立性检验 ，检验统计量为皮尔森的卡方统计量；
若是 无相关检验，则值为 $$=\frac{相关系{数}^2\ast \sqrt{数据个数-2}}{\sqrt{1-相关系{数}^2}}$$

（6）拒绝域：拒绝域依置信水平α不同而变化。为对应置信水平的范围

（7）通过拒绝域判断假说：若检验统计量值在拒绝域之中，则结论为 “对立假说正确” ；反之，则结论为 “无法判定虚无假说为误”。
检验统计量的值即使在拒绝域中，单以 “检验” 并无法给出“对立假说绝对正确；但是，只能作虚无假说存在正确的机率。其值最大为（α*100%）“的结论

3、虚无假说和对立假说（单独讲解）

虚无假说中，被推论为并非 "总体的克莱姆相关系数的值 ‘越接近’ 于0 "，而是 “总体中的克莱姆相关系数的值为0” 的难以证明的假说。
即：难以证明的假说做为虚无假设，而和虚无假设对立的假设则称为对立假说
详细参考该链接

4、 P值和”检验“的顺序（单独讲解）

• 何为P值？
  依 “检验” 的种类不同，P值的思考方式也会不同；
  而 独立性检验的 P值 即为：在虚无假说为真的情况下，则本次求出的值为大于或等于 $x_0^2$ 值的机率
  以先前的例子来说，图中阴影部分就是该机率

为 “检验” 下结论时的根据有：
	（1）检验统计量是否在拒绝域中；
	（2）P值是否小于置信水平；

（1）在第二节已讲解，可回去查看
（2）使用P值检验，顺序与上面的有些不同：

• 检验统计量值对应的P值，是否比置信水平小；
• 所得的P值若小于置信水平，即可作出"对立假说正确"的结论，反之则结论为"无法判定虚无假说为误"；
• 即使P值小于置信水平，以"检验"并无法作出"对立假说绝对正确"的结论。只能作出"虽然想说对立假说绝对正确，但是只能作虚无假说存在正确的机率为（P值*100%）"的结论
  详细参考该链接

5、独立性检验和齐性检验

齐性检验 和 独立性检验 是非常相似的 “检验” 方法 ；
无论是否为独立性检验，其 “检验” 分析顺序均相同。👉详细参考该链接

6、检验的结论表现

详细参考该链接