These vector norms treat an mn
For example, using the p -norm for vectors, we get:
This is a different norm from the induced p -norm (see above) and the Schatten p -norm (see below), but the notation is the same.
The special case p p
[edit ] Frobenius norm
For p Frobenius norm Hilbert–Schmidt norm Hilbert space . This norm can be defined in various ways:
where A * conjugate transpose A , σi singular values A , and the trace function K n inner product
The Frobenius norm is submultiplicative numerical linear algebra . This norm is often easier to compute than induced norms.
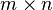
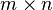


 1万+
1万+
 596
596

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


