[问题描述]:
设有n堆石子排成一排,其编号为1、2、3、…、n(n<=100)。每堆石子的数量用:a[1]、a[2]、…、a[n] 表示,现将这n堆石子归并成一堆,归并的规则:
◆每次只能将相邻两堆归并成一堆,即:第 1 堆石子 a[1] 只能与第 2 堆石子 a[2] 归并,最后一堆石子 a[n] 只能与 a[n-1] 归并,中间的石子 a[i] 只能与 a[i-1] 或 a[i+1] 归并;
◆每次归并的代价是两堆石子的重量之和。
我们假如5堆的石子,其中石子数分别为7,6,5,7,100
•按照贪心法,合并的过程如下:
每次合并得分
第一次合并 7 6 5 7 100 =11
第二次合并 7 11 7 100=18
第三次合并 18 7 100 =25
第四次合并 25 100 =125
总得分=11+18+25+125=179
每次合并得分
第一次合并 7 6 5 7 100 ->13
第二次合并 13 5 7 100->12
第三次合并 13 12 100 ->25
第四次合并 25 100 ->125
总得分=13+12+25+125=175
显然利用贪心来做是错误的,贪心算法在子过程中得出的解只是局部最优,而不能保证使得全局的值最优。
因此我们需要通过动态规划算法来求出最优解。
一:任意版
有N堆石子,现要将石子有序的合并成一堆,规定如下:每次只能移动任意的2堆石子合并,合并花费为的一堆石子的数量。设计一个算法,将这N堆石子合并成一堆的总花费最小(或最大)。
此类问题比较简单,就是哈夫曼编码的变形,用贪心算法即可求得最优解。即每次选两堆最少的,合并成新的一堆,直到只剩一堆为止。证明过程可以参考哈夫曼的证明过程。
所用的数据结构:
1、 是堆,取两次堆顶的最小元素,相加后再加入堆中,重复n-1次即可。
2、 两个队列,一个是原始的从小到大排序后的石子序列A。
一个合并后的石子生成的序列B,
注意:这两个序列都是有序的(从小到大),总是从它们中取出最小的两个相加到序列B。
二:直线版
在一条直线上摆着N堆石子,现要将石子有序的合并成一堆,规定如下:每次只能移动相邻的2堆石子合并,合并花费为将的一堆石子的数量。设计一个算法,将这N堆石子合并成一堆的总花费最小(或最大)。
如果熟悉矩阵连乘对这类问题肯定非常了解。矩阵连乘每次也是合并相邻两个矩阵(只是计算方式不同)。那么石子合并问题可用矩阵连乘的方法来解决。
那么最优子结构是什么呢?如果有N堆,第一次操作肯定是从n-1个对中选取一对进行合并,第二次从n-2对中选取一对进行合并,以此类推……
分析:我们熟悉矩阵连乘,知道矩阵连乘也是每次合并相邻的两个矩阵,那么石子合并可以用矩阵连乘的方式来解决。
设dp[i][j]表示第i到第j堆石子合并的最优值,sum[i][j]表示第i到第j堆石子的总数量。那么就有状态转移公式:
dp[i, j] = 0; (i=j)
dp[i, j] = min{ dp[i, k] + dp[k+1, j] } + sum[i, j]; (i != j)
public int minCost(int[] A) {
int n = A.length;
int[][] f = new int[n][n];
int[] sum = new int[n];
for(int i=0; i<n; i++) {
sum[i] = (i>0?sum[i-1]:0) + A[i];
}
for(int i=0; i<n; i++) {
Arrays.fill(f[i], Integer.MAX_VALUE);
f[i][i] = 0;
}
for(int w=2; w<=n; w++) { // sliding window size
for(int i=0; i<=n-w; i++) { // window start position
int j = i+w-1; // window end position
int sumij = sum[j] - (i>0?sum[i-1]:0);
for(int k=i; k<j; k++) {
f[i][j] = Math.min(f[i][j], f[i][k] + f[k+1][j] + sumij);
}
}
}
return f[0][n-1];
}
三:圆形版
如果石子是排成圆形,其余条件不变,那么最优值又是什么呢?
因为圆形是首尾相接的,初一想,似乎与直线排列完全成了两个不同的问题。因为每次合并后我们都要考虑最后一个与第一个的合并关系。直线版的矩阵连乘对角线式的最优子结构不见了。f(i, j)表示i-j合并的最优值似乎并不可行,因为我们可以得到的最优值第一步就是第一个与最后一个合并,那么f(i, j)并不能表示这种关系。
修改一下,f(i, j)表示从第i个开始,合并后面j个得到的最优值。sum(i, j)表示从第i个开始直到i+j个的数量和。那么这个问题就得到解决了。注意要把其看成环形,即在有限域内的合并。
破圆化直:将圆形的石子归并化为直线型石子归并。
方法是:将原来的石子长度增加一倍,加在原来的后面,a[1]~a[n],a[1]~a[n],
求从1,2,3,~n开始的n个合并的最小值,最其中一个最小值即可。
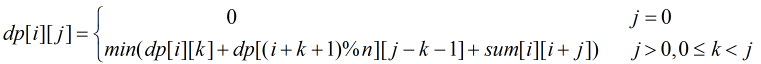
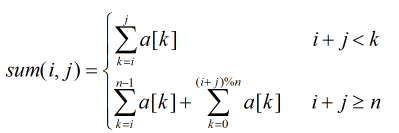
#
上面第二类与第三类的代码复杂度都是O(n^3),n为石子堆数目,那么还有没有复杂度更低的方法呢?有的。也是使用动态规划,由于过程满足平行四边形法则,优化后可以将复杂度降为O(n^2)。
Reference:
http://jsezzxl.wicp.net/Problem_Show.asp?id=1221
























 1008
1008

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








