【点云处理之论文狂读经典版6】—— Escape from Cells: Deep Kd-Networks for the Recognition of 3D Point Cloud Models

摘要

• Kd-Net根据KD树对点云进行细分，进行乘法变换并共享这些变换的参数
• Kd-Net不依赖于Grids
• 应用于shape classification, shape retrieval and shape part segmentation
• 代码详见https://github.com/fxia22/kdnet.pytorch

1.引言

• 索引结构：kd-trees、octrees、binary spatial partition trees、R-trees、constructive solid geometry, etc.
• 本文选择一种通用的3D索引结构kd-tree，设计了Kd-Net
• Kd-Net识别精度高、节省内存、计算效率高

2.相关工作

• Kd-net和RNN相关，它们都有树结构的计算图，但是RNN在计算树图中共享所有节点的参数，而Kd-net的参数共享更加结构化

3. Shape Recognition with Kd-Networks

3.1 输入

在训练时，Kd-Net处理的点云数量为$N=2^D$个，其中$D$为kd-tree的深度。一颗kd-tree $\mathcal{T}$通过自顶向下的方式进行递归构造，包含了$N-1=2^D-1$个非叶子节点。

每一个非叶子节点$V_i\in \mathcal{T}$都和三个划分方向 d i ∈ { x , y , z } d_i \in \left\{ {x, y, z} \right\} di​∈{x,y,z}和特定的划分位置${\tau }_i$相关联。一棵树的节点可以通过level l i ∈ { 1 … D − 1 } l_i \in \left\{ {1 \ldots D - 1} \right\} li​∈{1…D−1}进行表征，其中$l_i=1$为根节点，$l_i=D$包含了3D点。假设平衡树中的节点是以自上向下的方式进行标数的，即根节点是1，第$i$个节点的两个孩子为$c_1(i)=2i$和$c_2(i)=2i+1$。

3.2 Processing data with Kd-networks

给定一颗kd-tree $\mathcal{T}$，一颗训练好的Kd-Net会计算树中每个节点的向量表示${\mathbf{v}}_i$。对于叶子节点，每个点都会被表示成$k$维向量。对于非叶子节点的表示，通过自底向下的方式进行计算。

给定在$l$层的第$i$个非叶子节点$l(i)$，在第$l+1$层的孩子为$c_1(i)$和$c_2(i)$，孩子节点的表示${\mathbf{v}}_{c_1(i)}$ 和 ${\mathbf{v}}_{c_2(i)}$是已知的。那么，${\mathbf{v}}_i$可以通过下式计算：

$${\mathbf{v}}_i=\{\begin{array}{l}\varphi \left(W_{\mathrm{x}}^{l_i}\left[{\mathbf{v}}_{c_1(i)};{\mathbf{v}}_{c_2(i)}\right]+{\mathbf{b}}_{\mathrm{x}}^{l_i}\right),\text{ if }{d}_i=\mathrm{x},\\ \varphi \left(W_{\mathrm{y}}^{l_i}\left[{\mathbf{v}}_{c_1(i)};{\mathbf{v}}_{c_2(i)}\right]+{\mathbf{b}}_{\mathrm{y}}^{l_{\mathrm{y}}}\right),\text{ if }{d}_i=\mathrm{y}\\ \varphi \left(W_{\mathrm{z}}^{l_i}\left[{\mathbf{v}}_{c_1(i)};{\mathbf{v}}_{c_2(i)}\right]+{\mathbf{b}}_{\mathrm{z}}^{l_i}\right),\text{ if }{d}_i=\mathbf{z}\end{array}$$
或者是：
$${\mathbf{v}}_i=\varphi \left(W_{d_i}^{l_i}\left[{\mathbf{v}}_{c_1(i)};{\mathbf{v}}_{c_2(i)}\right]+{\mathbf{b}}_{d_i}^{l_i}\right).\text{\hspace{1em}(2)}$$

其中，$\varphi (\cdot )$是激活函数，$[\ast ,\ast ]$表示拼接。仿射变换是通过第$l_i$层的可学习参数$\left\{W_{\mathrm{x}}^{l_i},W_{\mathrm{y}}^{l_i},W_{\mathrm{z}}^{l_i},{\mathbf{b}}_{\mathrm{x}}^{l_i},{\mathbf{b}}_{\mathrm{y}}^{l_i},{\mathbf{b}}_{\mathrm{z}}^{l_i}\right\}$ 定义的。因此，基于节点的划分方向$d_i$，使用了三个仿射变换中的一个加上一个简单的非线性变换进行特征处理。

矩阵和偏移的维度是由树的每层表示的维度$m^1,m^2,\dots ,m^D$确定的。因此，在$l$层的矩阵$W_{\mathrm{x}}^l,W_{\mathrm{y}}^l$, 和 $W_z^l$ 的维度为$m^l\times 2m^{l+1}$ ，${\mathbf{b}}_{\mathrm{x}}^l,{\mathbf{b}}_{\mathrm{y}}^l,{\mathbf{b}}_{\mathrm{z}}^l$的维度为$m^l$。

按照上面的方法，根节点的表示${\mathbf{v}}_1(\mathcal{T})$可以通过自下而上的方式获得。如果要是在通过几层全连接，就可以进行分类任务：
$${\mathbf{v}}_0(\mathcal{T})=W^0{\mathbf{v}}_1(\mathcal{T})+{\mathbf{b}}^0,\text{\hspace{1em}(3)}$$

其中$W^0$和${\mathbf{b}}^0$是多类分类器的参数。

3.3 Learning to classify

Kd-Net是一个分别在$D-1$非叶子层上具有可学习参数$\left\{W_{\mathrm{x}}^j,W_{\mathrm{y}}^j,W_{\mathrm{z}}^j,{\mathbf{b}}_{\mathrm{x}}^j,{\mathbf{b}}_{\mathrm{y}}^j,{\mathbf{b}}_{\mathrm{z}}^j\right\}$的网络，其中 j ∈ { 1 … D − 1 } j \in\{1 \ldots D-1\} j∈{1…D−1}，还有$\left\{W^0,{\mathbf{b}}^0\right\}$被用于最后的分类器。

标准的反向传播方法可以计算损失函数的梯度，即网络参数。然后网络参数通过从已标注的kd-trees学习，所使用的方法包括随机梯度下降和标准的损失函数（cross-entropy）。

3.4 Learning to retrieve

公式3不仅学习类别的概率，还可以得到一个特定维度的描述向量，用于表征形状，从而进行retrieval。可用的损失函数包括：histogram loss ，Siamese loss，triplet loss

3.5 Properties of Kd-networks

• 每层间共享参数 Kd-Net在树的第$j$层中所有节点都共享乘法参数$\left\{W_{\mathrm{x}}^j,W_{\mathrm{y}}^j,W_{\mathrm{z}}^j,{\mathbf{b}}_{\mathrm{x}}^j,{\mathbf{b}}_{\mathrm{y}}^j,{\mathbf{b}}_{\mathrm{z}}^j\right\}$
• 分层表示 在一个特定层的空间位置表示是从之前那些层的周边位置表示得到的，特别地，Kd-net在kd-tree的相同层的不同节点间的感知域是不重叠的
• Non-invariance to rotations
• Role of kd-tree structure kd-tree结构在Kd-Net数据处理中的作用有两个：
  (1) kd-tree决定哪些叶子表示被组合/合并在一起，以及决定顺序
  (2) kd-tree 的结构可以被看作是一个形状描述子，因此可以作为信息的来源，而不用考虑叶子的表示

3.6 Extension for segmentation

本文采用带有skip connections的encoder-decoder结构。在前向传播时，表示${\mathbf{v}}_i$通过等式2计算，然后在每个节点$i$处都要计算表示向量${\tilde{\mathbf{v}}}_i$。在计算decoder的表示时，先设置${\tilde{\mathbf{v}}}_1={\mathbf{v}}_1$（或者通过一个或几个全连接层得到${\tilde{\mathbf{v}}}_1$），然后使用自顶向下的方法计算后面的表示：
$$\begin{array}{rl}& {\tilde{\mathbf{v}}}_{c_1(i)}=\varphi \left(\left[{\tilde{W}}_{d_{c_1(i)}^{l_i}}{\tilde{\mathbf{v}}}_i+{\tilde{\mathbf{b}}}_{d_{c_1(i)}}^{l_i};S^{l_i}{\mathbf{v}}_{c_1(i)}+{\mathbf{t}}^{l_i}\right]\right)\\ & {\tilde{\mathbf{v}}}_{c_2(i)}=\varphi \left(\left[{\tilde{W}}_{d_{c_2(i)}}^{l_i}{\tilde{\mathbf{v}}}_i+{\tilde{\mathbf{b}}}_{d_{c_2(i)}}^{l_i};S^{l_i}{\mathbf{v}}_{c_2(i)}+{\mathbf{t}}^{l_i}\right]\right)\end{array}$$
其中${\tilde{W}}_{d_{c_{\ast }(i)}}^{l_i}$ 和${\tilde{\mathbf{b}}}_{d_{c_{\ast }(i)}}^{l_i}$时仿射变换的参数，将父节点的表示映射到孩子节点表示。同时$S^{l_i}$和${\mathbf{t}}^{l_i}$也是仿射变换的参数，但计算的是从${\mathbf{v}}_{c_1(i)}$ 到 ${\tilde{\mathbf{v}}}_{c_1(i)}$的skip connection变换。前面的一组参数主要取决于划分方向，后面的一组参数仅取决于节点层。

3.7 Implementation details

• Leaf representation 在本文中，如果不是特别描述，将归一化的3D坐标作为Leaf representation。以形状的质心为中心，将形状的点云伸缩到$[-1;1{]}^3$ 的3D box即可。
• Data augmentation 在3D点云上应用几何变换。此外，在kd-tree结构中加入随机变化很有用，使用以下的概率来随机选择划分的方向：
  $$P\left(d_i=j\mid {\hat{\mathbf{r}}}_i\right)=\frac{\exp \gamma {\hat{r}}_i^j}{{\sum }_{j=x,y,z}\exp \gamma {\hat{r}}_i^j}$$
  其中，${\hat{r}}_i$是归一化为单位和的范围向量。

4.实验

4.1 Shape classification

采用均匀采样。测试的时候跑10次，取平均值

• 对于深度为10的kd-tree，叶子节点为32，中间表示的维度为：$32-64-64-128-128-256-256-512-512-128$
• 对于深度为15的kd-tree，叶子节点为8，表示的维度为：$16-16-32-32-64-64-128-128-256-256-512-512-1024-1024-128.$

用NVidia Titan Black，10层的模型跑16个小时；15层的跑5天。

Ablations and variants

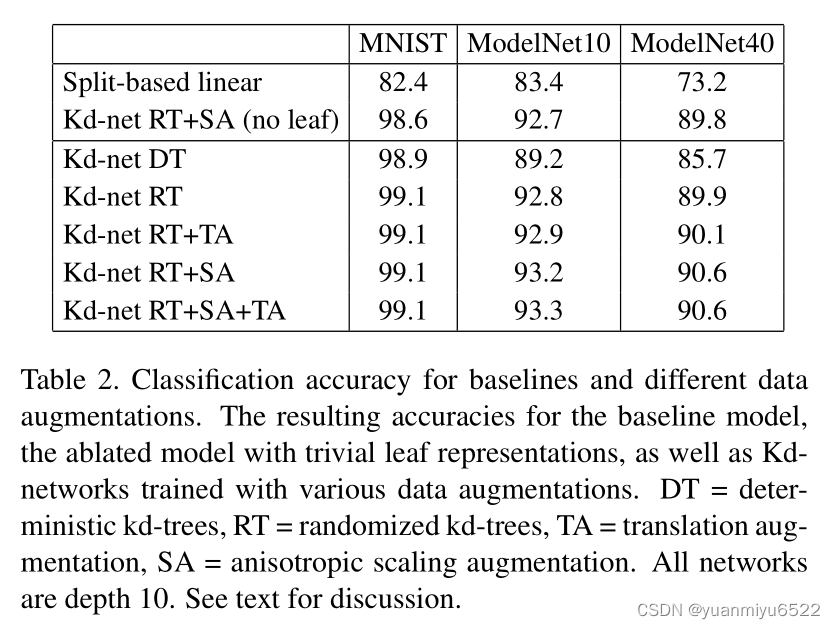
Kd-Net主要使用了每个形状的两个信息：

• leaf represenations
• direction of the splits

通过上表可以看出：

• Kd-Net的多步分层数据格式和权值共享方法还是很重要的。
• split direction要比 leaf represenations重要多了
• kd-tree的randomization所带来的提升很大，几何增强带来的提升很小

Kd-tree depth experiments

对 于较小的模型，每个epoch训练的时间很短，但是收敛时的epochs却很多。
对于较大的我模型，kd-tree的构造就很难。

非均匀采样和扰动时，模型会出现退化现象。

4.2 Shape retrieval

ShapeNetCore

分两步进行训练：

1. 网络首先按照分类任务进行训练
2. 移除最后的分类器，归一化点云的表示，得到形状描述子，使用带有histogram loss的网络进行微调

4.3 Part Segmentation

ShapeNet-part

Kd-Net在Part Segmentation上的性能不佳，可能是因为kd-tree中高层划分的信息传播不够，kd-tree在Segmentation任务上表现得不够好。

5.结论

除了kd-tree，其他的结构如octrees, PCA-trees, bounding volume hierarchies也可以研究，用于深度网络中。