Ivy 原网页:Invariants (microsoft.github.io)Invariants (microsoft.github.io)Invariants (microsoft.github.io)
该部分将学习如何制作一个简单协议的抽象模型,并使用归纳不变量证明其性质。这通常是在Ivy中设计和实现协议的第一步。
系统的不变量是一个关于系统状态的公式,它总是成立的。不变量是我们指定的关于系统的最简单的一类性质。归纳不变量是一个公式或一组公式,具有以下关键性质:
启动:在程序的所有初始状态下都是如此。
连续性:如果在一个状态下为真,那么在执行任何导出的操作后,公式保持为真。
-
initiation:在程序的所有初始状态下都是如此。
-
连续性:如果在一个状态下为真,那么在执行任何导出的操作后,公式保持为真。
每个归纳不变量都是不变量,但不是每个不变量都是归纳的。归纳不变量相对容易证明,因为我们只需要验证起始和连续性质,Ivy通常可以自动执行这项任务。然而,通常情况下,我们真正想要证明的不变量性质不是归纳的,因此我们需要一些聪明的方法来加强所需的不变量,使其成为归纳的。
正如我们将看到的,Ivy 通过提供工具来可视化归纳证明的失败,并建议对证明进行可能的改进,从而使这一步变得更容易。
一个抽象的协议模型
下面的 Ivy 程序是一个非常抽象的信号量协议模型。我们有一组客户端和一组服务器。每个服务器都有一个信号量,一次最多只能由一个客户端持有。
#lang ivy1.7
type client
type server
relation link(X:client, Y:server)
relation semaphore(X:server)
after init {
semaphore(W) := true;
link(X,Y) := false
}
action connect(x:client,y:server) = {
require semaphore(y);
link(x,y) := true;
semaphore(y) := false
}
action disconnect(x:client,y:server) = {
require link(x,y);
link(x,y) := false;
semaphore(y) := true
}
export connect
export disconnect下述是代码分块解释:
type client
type server这个程序声明了客户端和服务器两种类型。在这一点上,除了每种类型至少有一个值之外,我们对这些类型一无所知。客户端和服务器类型可以分别表示客户端和服务器的抽象标识符(当我们实现该协议时,我们可能会用网络地址替换这些抽象标识符)。
relation link(X:client, Y:server)
relation semaphore(X:server)协议模型的状态由两个关系组成。关系链接告诉我们哪些客户机持有哪些服务器的信号量,而信号量告诉我们哪些服务器具有“启动”的信号量(也就是说,可以使用)。
after init {
semaphore(W) := true;
link(X,Y) := false
}该程序在 init 之后的关键字后面包含一个块代码。当协议启动时,此代码只执行一次。它初始化状态,使所有信号量都是“up”(即,对于每个服务器 W。semaphore(W)设置为 true),并且没有链接(即,针对每个客户端 X 和服务器 Y,link(X,Y)设置为false)。这些语句是同时进行的赋值,一次更新其参数的许多值的给定关系。可以通过关系的参数是用大写字母表示的占位符(或通配符)这一事实来识别同步分配。
action connect(x:client,y:server) = {
require semaphore(y);
link(x,y) := true;
semaphore(y) := false
}
action disconnect(x:client,y:server) = {
require link(x,y);
link(x,y) := false;
semaphore(y) := true
}该程序将两个操作导出到环境:connect 和 disconnect。connect 操作创建了一个从客户端 x 到服务器 y 的链接,从而降低了服务器的信号量。
每个操作都有一个前提条件,由 require 关键字表示。要采取行动,就需要环境满足其前提条件。请注意,connect 要求服务器的信号量在最初启动。disconnect 操作会删除一个链接并打开信号灯。它要求最初建立链接。最后的两个导出声明告诉我们,环境可以按任意顺序调用 connect 和 disconnect,尽管它必须遵守规定的要求。
重要的是要记住,这个 Ivy 程序是协议的抽象模型,而不是协议的实际实现。抽象操作只是描述了协议可以进行的可能的高级状态转换。它并没有告诉我们这些转变实际上是如何发生的。在实现中,抽象连接操作可以通过客户端向服务器发送请求消息,服务器发出回复来实现。
Safety and invariant conjectures
现在将给抽象模型一个它必须满足的性质。可以指定的最简单的一种属性是不变量。这是一个公式,在环境对程序操作的调用之间必须保持正确(尽管在执行操作时可能暂时不正确)。在上面的客户端/服务器示例中,可能会指定不能将两个不同的客户端同时链接到单个服务器。可以使用以下不变断言来表达此属性:
invariant ~(X ~= Z & link(X,Y) & link(Z,Y))大写字母再次充当通配符。不变断言隐式地适用于所有客户端 X 和 Z 以及所有服务器 Y。另一种说法是占位符 X、Y 和 Z 隐含地普遍量化。
Proving the invariant
如上所述,为了证明一个不变量,检查它最初是否为真,并且程序的每个操作都会保留它。Ivy 可以自动做到这一点。要进行检查,使用以下命令:
$ ivy_check client_server_example.ivy[ 注意:本教程中示例的源文件可以在 Ivy 源树的子目录 doc/examples ] 中找到。Ivy 尝试进行检查,并产生了一些令人沮丧的输出(省略了不感兴趣的部分):
...
Initialization must establish the invariant
client_server_example.ivy: line 30: invar2 ... PASS
...
The following set of external actions must preserve the invariant:
ext:connect
client_server_example.ivy: line 30: invar2 ... FAIL
ext:disconnect
client_server_example.ivy: line 30: invar2 ... PASS
...
error: failed checks: 1这意味着提出的不变量可能是真的,但它不是归纳的。特别是 connect 操作没有保留不变量。Ivy 可以给我们一些反馈,以反例的形式解释出了什么问题。这种情况下的反例是 connect 动作的执行,该动作在不变量为 true 的状态下开始,在不变量为 false 的状态下结束。
可以通过使用选项 diagnose=true 再次运行检查来获得反例的图形视图,如下所示:
$ ivy_check diagnose=true client_server_example.ivyIvy弹出一个窗口,看起来像这样:

在该窗口的左窗格中是一个图表,其中每个椭圆形表示协议的状态,每个箭头表示操作的执行。有两种状态,分别标记为 0 和 1。从状态 0 到状态 1,有一个标有 connect 操作的箭头。我们知道 connect 的执行出现了问题。
在中间窗格中,我们看到状态 0 的图形表示。目前,我们看到的是有两个客户端(换句话说,两个类型为 client 的值)和一个服务器。要了解有关该状态的更多信息,我们可以使用右侧的复选框来启用此状态下关系的显示。例如,如果我们选中关系 link(X,Y) 旁边 + 列中的框,当关系 link(X,Y) 为 true 时,我们将看到从客户端 X 到服务器 Y 的箭头。在这种情况下,我们可以看到:
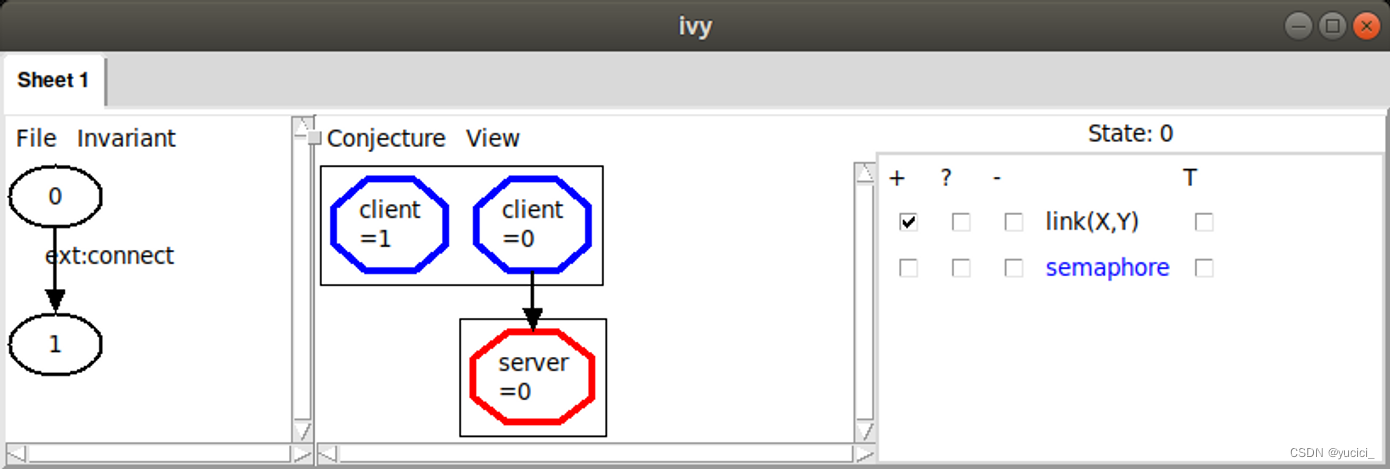
在这里,我们看到只有一个客户端连接到服务器,这意味着我们的不变属性是真的。当我们检查不变量是归纳的时,反例总是从不变量成立的状态开始。如果我们选中 semaphore(X) 旁边 + 列中的框,我们可能会开始看到一个问题:

Ivy 告诉我们,我们服务器上 semaphore 的值是 true。然而,我们已经考虑到,每当客户端连接到服务器时,信号量都应该是“down”(即 false)。因此,我们怀疑系统的这种状态是不可能的(也就是说,从初始状态无法达到)。这通常意味着我们需要在不变量中添加另一个公式,以排除这种状态的一些不好之处。
要查看信号量 up 的结果,我们可以点击它进入状态 1:

现在,两个客户端都链接到同一个服务器,这违反了我们的不变属性。归纳法的反例总是以这种方式结束的。要了解我们是如何到达那里的更多细节,我们可以右键单击动作 connect 并选择“ Step in ”。这将向我们展示导致坏状态的详细操作顺序:
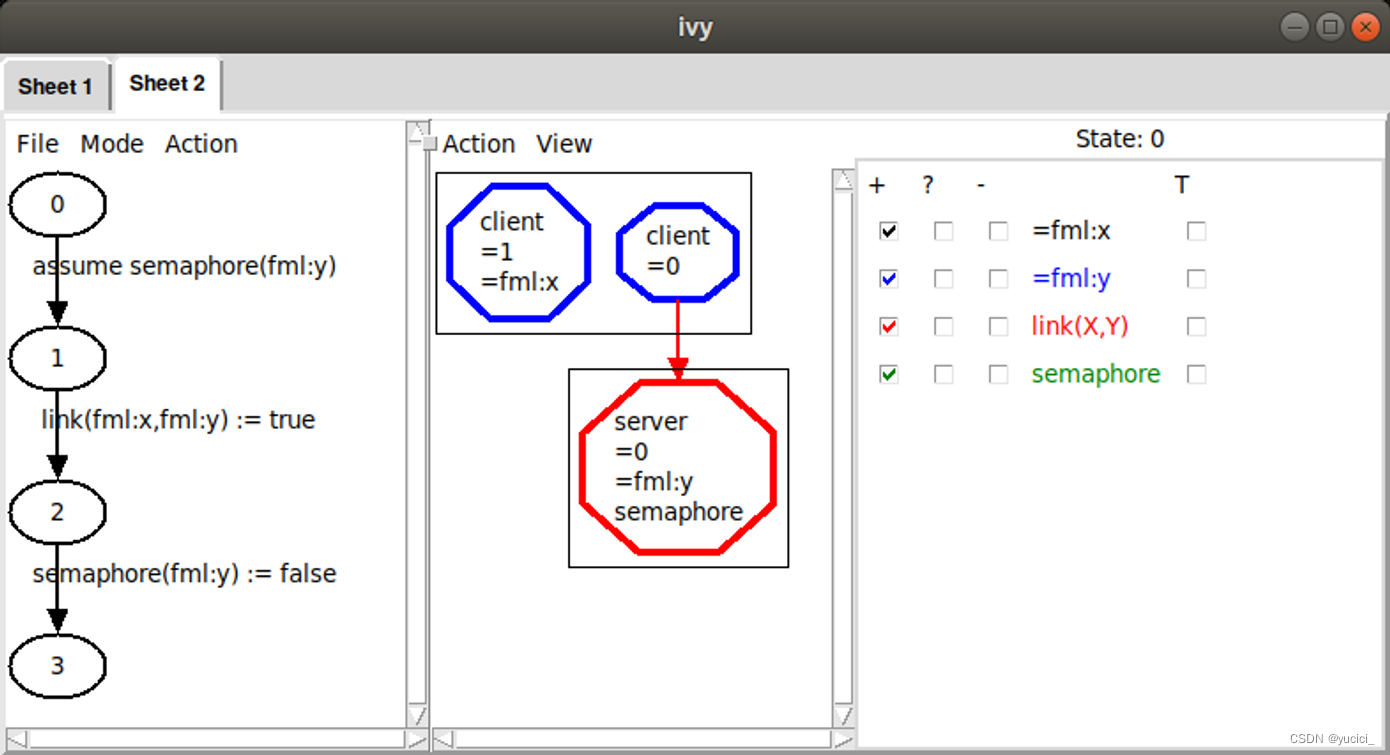
在这里,我们正在查看状态 0(仅在进入连接操作时发生的状态)。我们选中了几个框来显示有关此状态的信息。我们可以在这里看到环境在调用 connect 时提供的形式参数 x 和 y 的值。特别是,环境为 x 选择了值 1,这意味着客户端 1 应该连接到服务器 0(本例中唯一的服务器)。这个反例通过三个额外的状态,首先测试 connect 的前提条件(这是真的,因为信号是 up 的),然后建立一个从 x 到 y 的链接,然后把信号 down。
如果我们右键单击 any statement 选择“ Show source ”,则会显示相应的源代码行。当我们进入动作调用时,我们构建了一系列选项卡,对应于程序执行的堆栈跟踪。可以通过从“ File menu ”菜单中选择“ Remove tab ”来删除选项卡。
在这一点上,我们理解了不变量不是归纳的原因。故障是由于客户端 X 连接到服务器 Y,并且该服务器上的信号量 up。这种糟糕的模式导致了失败,我们推测它永远不会真正发生。出于这个原因,我们将用一个排除坏模式的条件来加强我们的不变量。非常重要的是要理解,我们不想排除所有不现实的反例——只想排除那些真正导致失败的方面。
为了排除坏模式,我们在 Ivy 程序中添加了这个新的推测不变量:
private {
invariant ~(link(X,Y) & semaphore(Y))
}这意味着没有客户端 X 和服务器 Y,因此 X 被链接到 Y,并且 Y 处的信号量是 up。再次注意,大写字母X和Y是通用的量化占位符。我们将新的不变量属性放在私有部分中,只是为了表明协议模型的用户对这个不变量不感兴趣。它只是作为原始不变量证明的一部分引入的。现在,当我们检查程序时,我们会得到以下信息:
...
Initialization must establish the invariant
client_server_example.ivy: line 26: invar2 ... PASS
client_server_example.ivy: line 34: invar3 ... PASS
Any assertions in initializers must be checked ... PASS
The following set of external actions must preserve the invariant:
ext:connect
client_server_example.ivy: line 26: invar2 ... PASS
client_server_example.ivy: line 34: invar3 ... PASS
ext:disconnect
client_server_example.ivy: line 26: invar2 ... PASS
client_server_example.ivy: line 34: invar3 ... PASS
...
OK末尾的 OK 告诉我们,我们的不变量加在一起现在是归纳的。这意味着我们可以确信不变量总是成立的。
另一种从坏模式创建推测不变量的方法是让 Ivy 收集显示的事实并对其进行归纳。一旦我们显示了错误的模式,如上所述,我们使用“ Conjecture ”菜单中的“ Gather ”命令。这给了我们以下信息:

Ivy 收集了关于显示状态的三个事实,显示在“ Constraints ”标题下。这些事实是我们以图形方式观察到的坏模式的逻辑表示:有两个不同的节点,其中一个连接到服务器,服务器的信号量 up。
还请注意,图中的一些节点和圆弧已高亮显示,以表明它们在列出的 facts 中使用。我们可以点击这个列表中的 facts 来切换它们。这允许我们调整坏模式。
由于我们认为所显示的事实形成了一个不好的模式,我们可以对它们进行概括,以产生一个关于程序状态的新的猜想不变式。从 Conjecture 菜单中选择 Strengthen 选项,我们看到:

Ivy 建议将这个事实添加到 conjectured invariants 的列表中:
~(C:client ~= D & link(C,S) & semaphore(S))Ivy 只是用普遍量化的占位符 C、D 和 S 替换了收集到的事实中的固定客户端和服务器标识符。这个公式表明,我们不能有两个不同的客户端,其中一个客户端连接到服务器,而信号量则处于 up 状态。我们单击“确定”,将这个公式添加到我们的 conjectured invariants 列表中。
我们现在可以尝试用我们的新猜想再次检验归纳性。我们使用“ Invariant ”菜单中的“ Check induction ”命令来完成此操作。我们看到以下内容:

如果归纳检查失败,我们将看到一个新的反例,我们将不得不排除。然而,由于它是成功的,我们现在有了一个证据,证明我们想要的不变量成立。当然,我们想保存我们新的归纳不变量,这样我们以后可以再次使用它。我们从“ File ”菜单中选择“ Save invariant ”,然后输入文件名:

以下是文件的内容:
# new conjectures
invariant ~(C:client ~= D & link(C,S) & semaphore(S))这个新的不变量可以粘贴到我们的程序中。请注意,它与我们之前选择的不变量略有不同。也就是说,坏模式包括违反互斥的期望属性所需的第二客户端 D。事实证明这并不重要。这个较弱的不变量仍然足够强,足以证明这个性质。
让我们来考虑一下我们刚刚用来得到一个归纳不变量的过程。我们采取了以下步骤:
- 找到一个简单的反例
- 识别反例(坏模式)的相关事实
- 推广形成普遍量化不变猜想
第一步和最后一步是 Ivy 自动完成的。但是,我们手动执行了第二步,即选择要显示的关系。
这个过程是一门艺术,可能令人困惑。例如,有时我们认为是坏模式的条件实际上是可以达到的。在这种情况下,我们必须回溯,也许可以排除更具体的模式。幸运的是,Ivy 提供了一些工具来帮助我们做出这些选择。
Generalization tools
Ivy内置了一些技术来帮助我们识别坏模式(反例)。让我们回到我们发现的对我们提出的不变量的归纳性的反例:

我们可以要求 Ivy 尝试从反例中进行推广,在状态 0 中找到一个坏模式,该模式足以导致我们提出的不变量在状态 1 中失败。为此,我们从“ Invariant ”菜单中选择“ Diagram ”。这将产生以下显示:
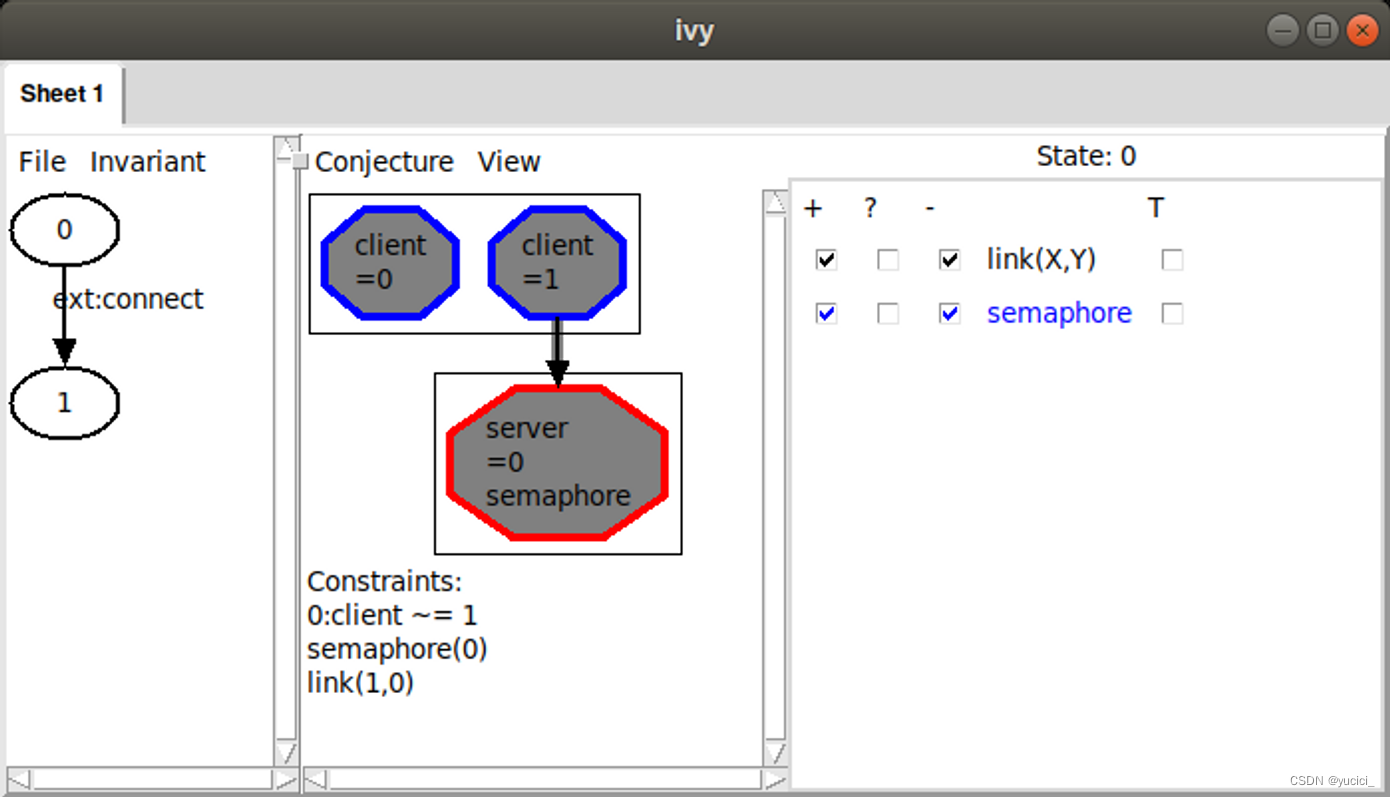
Ivy 已经绘制了一张图表,显示了它在该状态发现的一种可能的不良模式。该模式包括我们的反例中的两个客户端和服务器,它们在图中突出显示。此外,它还包括从客户端 1 到服务器的链接,以及信号量在服务器上为真的事实。这些事实列在图表下方的“ Constraints ”标题下。Ivy 已经确定这些条件足以导致不变量失效。
由于我们同意这是一个糟糕的模式,我们可以使用“ Conjecture ”菜单中的“ Stengthen ”选项,如上所述,生成一个排除它的推测不变量。在这种简单的情况下,不变量的增强是完全自动完成的。
然而,正如我们上面所指出的,这个坏模式包含了不相关的事实,我们可能想放弃它,以得到一个更强大的猜想,排除更多的情况。也就是说,我们的坏模式要求有两个不同的节点,即 0 和 1。事实上,我们确实需要两个节点才能有安全违反(即有两个节点连接到一个服务器)。不过请注意,如果我们从模式中去掉这个事实,我们仍然有一个可以排除的模式,即 semaphore(0 )和 link(0,0)。
为了验证这个想法,我们通过点击从模式中删除不相关的事实。不需要的事实变成灰色:

当我们加强使用这种模式时,我们会得到:

也就是说,我们的新推测表明,没有任何客户端可以在信号灯打开的情况下连接到服务器,但这并不取决于任何其他客户端的存在。我们可以用这个猜想来验证,我们仍然有一个归纳不变量。
这说明了关于归纳不变量的一个重要观点:归纳不变量有很多。这使我们能够灵活地找到一个简单的方法。通过从坏模式中去掉一个事实,我们有效地推广了它。也就是说,我们排除了一大类状态,所以实际上我们做出了更有力的推测。
Ivy 经常会自动发现,一个糟糕的模式可以被简化。一种方法是使用有界可达性。Gather 后,我们可以从“ Conjecture ”菜单中选择“ Minimize ”,而不是手动消除不需要的事实。Ivy 询问要检查的步骤数。有点武断,我们选择四个。这是我们得到的结果:

Ivy 已经认识到,如果我们只考虑协议执行的四个步骤,就可以排除更普遍的模式。它的推测是,如果任何客户端连接到服务器,那么该服务器的信号量就会停止。经过四个步骤的执行,这个事实肯定是正确的,但这仍然是一个猜测。如果我们怀疑这可能不是一成不变的事实,我们可以尝试五步、六步等等,直到我们确信,或者直到常 Ivy 变得太慢。
我们可以使用 Strengthen 将 Ivy 的广义猜想添加到我们的集合中,这就完成了证明。
Things that go wrong
在某个时刻,我们会做出一个完全错误的猜测,因为它并不总是正确的。在单击“ Strengthen ”之前,最好尝试“ Bounded check ”,看看所提出的坏模式是否真的会在一定数量的步骤内发生。
为了了解情况,假设我们进入这种情况:

在这里,我们没有考虑信号量,我们推测了一个错误的模式,其中有一个客户端连接到服务器。显然(或者希望)这实际上是可以实现的。要了解为什么这是一个糟糕的推测,我们可以从“ Conjecture ”菜单中选择“ Bounded check ”。以下是我们选择一个步骤时看到的内容:

Ivy 尝试了节点客户端连接到任何服务器的猜测一步,但发现这是错误的。如果我们单击“ View ”,以下是我们看到的内容:

Ivy 在界面中创建了一个新的选项卡,其中包含两个步骤。箭头表示使用 ext 操作从状态 0 转换到状态 1。这代表了环境的作用。单击状态 0,检查 link 和 semaphore 的关系,我们看到以下内容:
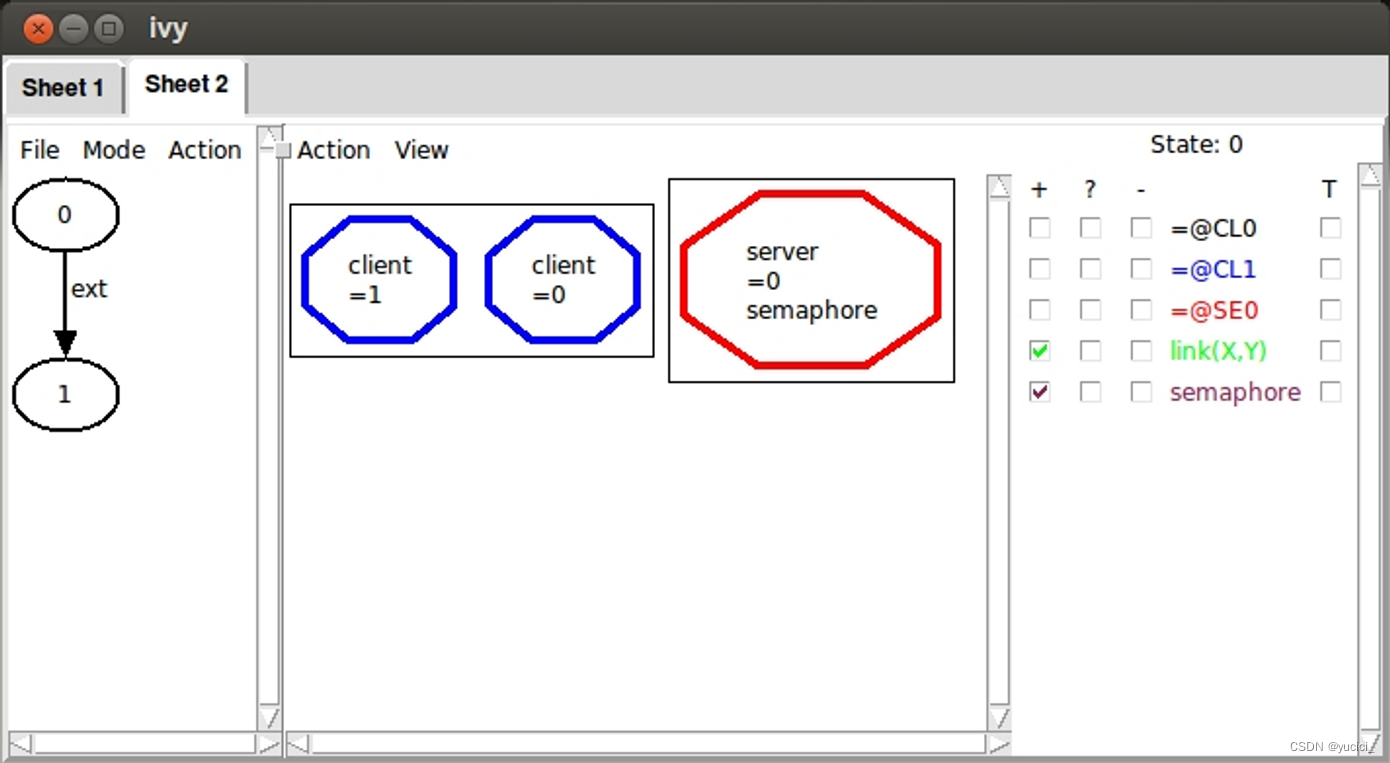
也就是说,在初始状态下,有两个客户端和一个服务器,服务器的信号量已启动,并且没有链接。
现在,点击状态 1,我们看到了我们提出的坏模式。这意味着这种模式实际上可以发生。

Removing a failed conjecture
即使使用有界检查,我们仍然有可能错误地用一个不正确的猜想来加强不变量。如果发生这种情况,或者如果我们因任何其他原因对某个推测感到遗憾,我们可以使用 Invariant 菜单中的 Weaken 操作将其删除:

可以调整此对话框的大小以查看长公式。
Summary
我们用归纳法证明了不变量。如果我们提出的不变量不是归纳的,Ivy 会生成一个归纳或 CTI 的反例。Ivy 试图提出最简单的反例。
CTI 可以通过加强所提出的归纳不变量来消除。为了做到这一点,我们在 CTI 中发现了一个坏模式。这是通过以下步骤完成的:
- 使用复选框显示相关信息
- Gather 显示的事实
- 通过单击启用或禁用来选择相关事实。
- 通过推广坏模式来 Strengthen 不变量。
在这个过程中,你可以从Ivy那里得到一些帮助:
- 使用图表让 Ivy 尝试猜测一个错误的模式。
- 使用 Bounded check 查看坏模式是否可以在给定的步骤数内到达。
- 使用 Minimize 可以通过删除不需要的事实来概括模式。
要调试反例,请左键单击操作调用并选择“ Step in ”。View source 操作可用于在源文件中查找操作。
当你确信应该排除坏模式时,使用 Strengthen 将其推广到一个普遍猜想,并将其添加到所提出的不变量中。要从所提出的不变量中移除一个猜想,请使用 Weaken。
当 Check induction 不产生 CTI 时,推测的不变量实际上是一个安全不变量。您可以通过 Save invariant 操作将其保存以备将来使用。

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








