根号算法：分块

• 导入

众所周知，我们熟悉的算法时间复杂度有常数级，对数级、线性级、次方级、指数级等等，其中为应对题目规模对时间复杂度的要求，我们一般要将算法的时间复杂度优化到对数级，但是实际上我们还有一种优化方法——根号算法，它的时间复杂度为级，同样可以应对大部分的题目规模，并且具有相当大的可拓展性。和对数算法基本对应分治类似，根号算法也对应着一种操作，就是本篇博客要介绍的分块。

• 什么是分块？

分块顾名思义，就是将数据分为一块一块，然后在每一块中单独解决问题后累计答案。但是这么思考的话，将一个问题分开解决和一起解决好像没什么区别吧。如果你要是这么想，那你的分治法肯定没学到精髓，对于分块的另一项重要应用——莫队算法的学习理解也会有难度。

其实分块真正巧妙的地方在于：对于一次修改或询问，它所覆盖到的每一个完整的块我们都是可以做一个整体处理，将其打上或查询其修改标记（类似于线段树里的懒标记），而不是一个一个数据的操作，这样对于一个块的操作就能在O(1)的时间内完成；而左右两边没有没完全覆盖的区间因为数据不多（不会超过两个块的数据范围），直接暴力处理就行了。最后讨论下时间复杂度：假设我们共有n个数据，分块大小为m，那么最多只有个块；一次修改或查询最多执行O(1)*块数(m)+两个不完整块(<2*n/m)次，我们近似为  次，这样很简单地利用均值不等式得到：当m取时，执行次数最少，这也就是根号算法的含义所在，当然对于不同题目，我们对一个块的操作可能不能在O(1)的时间内完成，这样我们需要根据分块思想自己推导出最后的时间复杂度的公式，再利用均值不等式得到最佳分块的大小，关于分块大小这点可以参考国家队大佬的论文，分析得相当详细（2017年《非常规大小分块算法初探》----徐明宽），如果实在不会，那就每道题都取吧，这样得到的时间复杂度也不会太差，也基本能够应对大部分的题面了。

上文只是非常模糊的讲了一下分块的基本思想，刚接触分块的读者肯定是无法立刻理解的，所以下面我们就一起来解决一道很经典的分块入门题目来更深入的理解这个算法：

题目链接：（https://loj.ac/problem/6278）

大意：给出一个长为n的数列，以及n个操作，操作涉及区间加法，询问区间内小于某个值x的元素个数。

下面我们以下面的一组数据为例：

5

7

9

3

8

6

1

4

2

为实现分块，我们需要储存一些数据：原数组num[n]，数据所在块序号pos[n]，块block[]，修改标记tag[]，其中pos[n]与block[]可以预处理：（block也可用普通的二维数组代替，但用vector能支持如插入等更多操作，同时不只是vector，它可以是任何数据结构如set，map等，这样分块能维护的功能也就相应的增加了）。然后根据题目的询问，我们思考一下，如何快速知道一个序列中小于某个值的元素个数？直接暴力搜索？好像可行，但可惜多次搜索势必会爆时间。哎，其实我们用的优化方式真的不多，既然O(n)的时间复杂度不行，O(1)的时间复杂度又不可能实现，就只剩下O(logn)了，那就必然是二分法了。二分法要求整个序列是有序的，所以我们要先将序列排个序，不过要注意分块是分别在每一块中操作，所以排序也应该是分别在每一块中排序，这部分代码如下：

typedef long long ll; 
const int N = 50005;
int num[N], pos[N], tag[225];
vector<int> block[225];
int m;
······
此处是修改与查询函数，见下文
······
int main(){
    int n; 
    scanf("%d",&n);
    m = sqrt(n);
    for(int i=1; i<=n; i++)
        pos[i] = (i-1)/m+1; //预处理每个点所在的块
    for(int i=1; i<=n; i++) {
        scanf("%d",&num[i]);
        block[ pos[i] ].push_back(num[i]); //将数据num[i]存入所在的块pos[i] 
    }
    for(int i=1; i<=pos[n]; i++)
        sort(block[i].begin(),block[i].end()); //对每一块分别排序
    ······
    此处是读取询问的代码，省略
    ······
    return 0;
}

现在，数据已经成功被我们分好了块：

5                       7                        9

3                     6                     8

1                       2                      4

                           第一块                                                      第二块                                                    第三块

block[1]={5, 7, 9}     block[2]={3, 6, 8}     block[3]={1, 2 ,4}

接着，我们考虑如何实现区间修改。

仔细理解上文中的这句话：“覆盖到的每一个完整的块我们都是可以做一个整体处理，将其打上或查询其修改标记（类似于线段树里的懒标记）”。假定我们要在区间[3,8]加上一个值x，这个修改区间覆盖了整个第二块，然后还覆盖了第一块和第三块的一部分。那么，根据原则，我们直接将第二块打上标记：tag[2]+=x，表示第二块中每个值都要增加x；而对于没有完整覆盖的两块，我们直接将它的原数组加上x：num[3]、num[7]、num[8]+=x，但此时要注意我们修改了原数组的值，这样它们所在的块就不再是有序的了，我们要将其重新排序。

void resort(int pos) { //重新排序
    block[pos].clear();
    for (int i = (pos - 1) * m + 1; i <= pos * m; i++)
        block[pos].push_back(num[i]);
    sort(block[pos].begin(), block[pos].end());
}
void modify(int l, int r, int x) {
    if (pos[l] == pos[r]) {  //在同一块内,直接暴力修改
        for (int i = l; i <= r; i++) num[i] += x;
        //原数组被修改，需要清空此块重新插入进行排序
        resort(pos[l]);
    }
    else {
        //整块打上标记
        for (int i = L; i <= R; i++)
            tag[i] += x;
        //非整块直接暴力
        for (int i = l; i <= pos[l] * m; i++) num[i] += x;
            resort(pos[l]);
        for (int i = R * m + 1; i <= r; i++) num[i] += x;
            resort(pos[r]);
    }
}

最后的查询与修改异曲同工，对于每个完整块就采取上文讲的二分查找答案，不完整块还是直接暴力，只是要注意tag标记的影响就行了。

int query(int l, int r, ll v) {
    int ans = 0;
    if (pos[l] == pos[r]) {
        for (int i = l; i <= r; i++)
            if ((ll)num[i] + tag[pos[i]] < v)
                ans++;
        return ans;
    }
    //完整块二分查找答案
    for (int i = L; i <= R; ++i)
        ans += lower_bound(block[i].begin(), block[i].end(), v - tag[i]) - block[i].begin();
    //不完整块直接暴力
    for (int i = l; i <= pos[l] * m; i++)
        if ((ll)num[i] + tag[pos[i]] < v)
            ans++;
    for (int i = R * m + 1; i <= r; i++)
        if ((ll)num[i] + tag[pos[i]] < v)
            ans++;
    return ans;
}

• 分块查找

我们目前已经掌握了一种快速查找的算法——二分查找，其查找效率高达logn，已经相当优秀了，这里介绍另一种还不错的查找方法（尽管我们应该不会去用它，不过还是大概了解下嘛~）——分块查找，借此再来加深下对分块的理解。

分块查找同样要求数据是有序的，不过它只要求每个块之间是有序的。什么意思，即对于单独一个块，我们不需要里面的元素有序，但是里面的元素必须要在一个范围内，而这个范围是有序的：

3    2    5

7    8    10

13   11   14

16   20   18

第一块里面的数据在2~5之间，第二块的数据在7~10之间，第三块的数据在11~14之间，第四块的数据在16~20之间，这里对块来说，应该是呈一个升序排列。而我们查找时要引入一个索引表：

                                                 

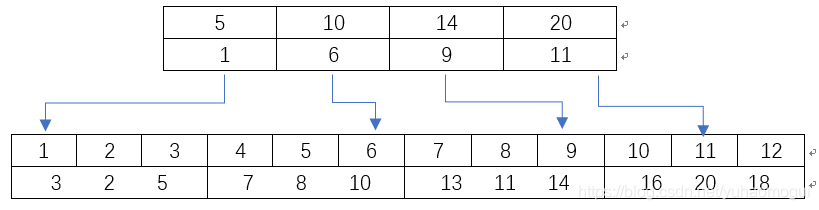
查找操作很简单，对于要求的查找值，在索引表中顺序查找，如果块数太多就改为二分查找，确定该数据所在的块，然后在该块中顺序查找就行了。

对于后续数据的插入，直接将其插入到所在范围的块中即可，因为不需要排序嘛，块的范围可以被扩大，但是不能与后面块的范围重叠，删除操作也类似。另外这里要注意，多次插入可能会导致每一个块的大小过大，降低查找效率，所以需要重新分块（这个地方要引起注意，涉及到插入的题都应该考虑到这点，而不仅仅是这里）。

• 写在后面

分块就介绍这么多了，最后补充一点，分块的可拓展性极强，能够应对几乎所有的区间问题（除了被卡时间···），其操作不是一篇博客能写完的，只能靠自己去慢慢摸索了。对于后续的学习，博主的建议是：

首先，学习下国家队大佬对分块的见解，指路：2013年国家集训队论文《浅谈分块思想在一类数据处理问题中的应用 》----罗剑桥 、《分块方法的应用》----王子昱、2014年国家集训队论文《根号算法——不只是分块》----王悦同 、2015年国家集训队论文《浅谈分块在一类在线问题中的应用》----邹逍遥。

然后，当然就是不断刷题了·······

• 例题

分块入门1~9，链接：loj problem6276~6285（https://loj.ac/problem/6276）。