(持续更新,欢迎交流)
1、最长公共子序列
用动态规划的方法解
#encoding=utf-8
class Solution:
def lcs(self,arr1,arr2):
len1=len(arr1)
len2=len(arr2)
bp1=[[0 for i in range(len2+1)]for j in range(len1+1)]#存路径
bp=[[0 for i in range(len2+1)]for j in range(len1+1)]#存动态规划的最大值
for i in range(1,len1+1):
for j in range(1,len2+1):
if arr1[i-1]==arr2[j-1]:
bp[i][j]=bp[i-1][j-1]+1
bp1[i][j]='ok'
elif bp[i][j-1]>bp[i-1][j]:
bp[i][j]=bp[i][j-1]
bp1[i][j]='left'
else:
bp[i][j]=bp[i-1][j]
bp1[i][j]='up'
return bp,bp1
def main(self):
a='ABCBDAB'
b='BDCABA'
arr1=list(a)
arr2=list(b)
bp,bp1=self.lcs(arr1,arr2)
res=[]
len1=len(arr1)
len2=len(arr2)
while(len1!=0 and len2!=0):
if bp1[len1][len2]=='ok':
res.append(len1)
len1-=1
len2-=1
elif bp1[len1][len2]=='left':
len1-=1
elif bp1[len1][len2]=='up':
len2-=1
res=res[::-1]
for item in res:
print arr1[item-1]
s=Solution()
s.main()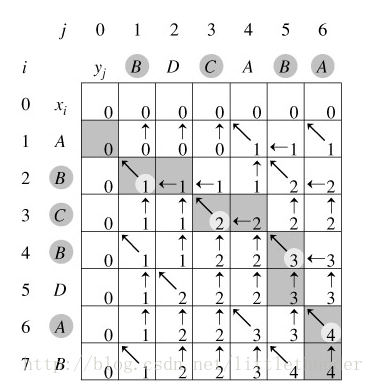
2、最长递增子序列
对于子序列[1,5,8,2,3,4]的递增子序列[1,2,3,4]。
该问题可以转化为求[1,5,8,2,3,4]和[,1,2,3,4,5,8]的最长公共子序列问题。








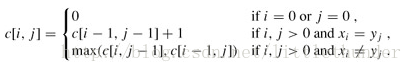

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








