Leetcode 之 Count Complete Tree Nodes

问题来源：Count Complete Tree Nodes
问题描述：给定一棵完全二叉树，求树的节点个数。完全二叉树就是把满二叉树右侧的叶子节点删掉几个构成的二叉树。
该问题一看就不能用传统的递归遍历或者层次遍历来统计节点个数，因为这没有利用到完全二叉树的性质，估计提交会超时。所以我们需要另辟蹊径，想想如何利用完全二叉树的性质来统计节点个数。

解法一

面对树的问题，我们首先想到的思路就是采用递归。针对该问题也可以采用递归实现（当然不是遍历所有节点的递归），不过在递归的时候需要我们发现完全二叉树的一个性质：完全二叉树左子树和右子树的高度要么相同要么只相差1，如图1所示。如果左子树和右子树的高度相同，则可以知道左子树一定是一棵满二叉树，从而我们可以根据高度计算出左子树中节点的个数，此时右子树是一棵完全二叉树，我们可以递归计算右子树的节点个数；相反的，如果左子树的高度比右子树大一，则说明右子树是满二叉树，我们可以直接计算右子树中节点的个数，此时左子树是一棵完全二叉树，我们也可以通过递归计算出其节点个数。

按照上面描述的思路递归实现完全二叉树节点个数统计的代码如下：

int getHeight(TreeNode* root)
{
    int height=0;
    while(root)
    {
        height++;
        root=root->left;
    }

    return height;
}

int countNodes(TreeNode* root) {
    if(!root) return 0;

    int lh=getHeight(root->left);
    int rh=getHeight(root->right);

    if(lh==rh)
    {
        return (1<<lh)+countNodes(root->right);
    }
    else
    {
        return (1<<rh)+countNodes(root->left);
    }
}

能想到思路，写出上面的代码难度不大，不过要分析上述代码的复杂度略微复杂，我们简单推导一下。获得左子树和右子树的高度复杂度是$O(logN)$，这块是比较容易理解的。假设N为完全二叉树的节点个数，T(N)为计算复杂度，则我们可以有如下递推式：

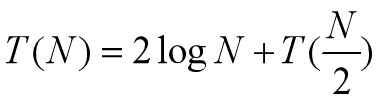
上述公式的含义是：针对规模为N的问题，我们首先用两次$logN$的操作获取左右子树的高度，然后针对两种情况我们都只需要解决一半规模的子问题即可获得原问题的解。把上面的公式进一步展开得到：

上述公式在展开的时候并不是无穷多项，因为我们必须要保证$log(N/k)$大于0，从而迭代$logN$次展开就结束了。经过简化我们可以知道上述算法的复杂度是$O(lo{g}^{2}N)$。假设树中的节点个数N为$2^k$,则直接遍历和上述方法之间的时间关系大概为

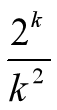
当N较小时该算法并不占优势，但是当N很大时该算法比直接遍历所有节点要快很多。上述方法非常巧妙，建议大家好好理解并掌握该方法。

解法二

后来从题解中又发现另一种非常巧妙的方法，居然将二分查找融合进来。给定一棵完全二叉树，我们可以很容易知道该树的高度h，也很容易知道最后一层元素个数的范围$[1,2^{h-1}]$，基于此我们可以设法通过二分查找的手段来获取最后一层到底有多少节点。问题的关键在于如何知道最后一层的第k个节点是否存在，我们只能从根节点开始往下遍历，按照某种规则恰好遍历到第k个叶节点。规则非常巧妙，将叶节点的编号和左右遍历的顺序对应起来。从根节点往下遍历，往左遍历赋值0，往右遍历赋值1，到叶节点我们就会生成一个二进制字符串，该串恰好对应叶节点的编号。例如叶节点3，对应的遍历顺序恰好是011。借助这个规则我们就可以从根节点遍历到任意的叶节点，从而使得二分查找成为可能。

此处使用二分查找和常规的二分查找略有不同，常规的二分查找我们是找到正确的元素，有时一次就可以找到，有时则需要迭代多次；在此的二分查找我们是要统计叶节点的个数，需要遍历到start和end重叠才行，迭代次数是固定的logN次。按照二分查找思路实现的代码如下：

int getHeight(TreeNode* root)
{
    int height=0;
    while(root)
    {
        height++;
        root=root->left;
    }

    return height;
}

int countNodes(TreeNode* root) {
    if(!root) return 0;
    if(!root->left) return 1;
    int height=getHeight(root);
    int nCount=1<<(height-1);
    int start=0,end=nCount-1;
    
    while(start<=end)
    {
        unsigned middle=(start+end)/2;//判断第middle个叶节点是否存在
        int mask=1<<(height-2);

        TreeNode* t=root;
        for(int i=0;i<height-1;i++)//找到对应的叶节点
        {
            if(middle&mask)
            {
                t=t->right;
            }
            else
            {
                t=t->left;
            }

            mask>>=1;
        }

        if(!t)
        {
            end=middle-1;
        }
        else
        {
            start=middle+1;
        }
    }

    return (1<<height-1)+end;
 }

该方法的时间复杂度也是$O(lo{g}^{2}N)$，其中n是完全二叉树的节点数。首先需要O(h)的时间得到完全二叉树的最大层数。使用二分查找确定节点个数时，需要查找的次数为$O(log{2}^h)=O(h)$，每次查找需要遍历从根节点开始的一条长度为h的路径，需要O(h)的时间，因此二分查找的总时间复杂度是 $O(h^2)$。因此总时间复杂度是$O(h^2)$。由于完全二叉树满足 $2^h\le n<2^{h+1}$，因此有 $O(h)=O(logn)$，$O(h^2)=O(lo{g}^{2}n)$。该方法思路也比较巧妙，但是在实现的时候需要特别注意变量的加减操作，此外二分查找要把end当做节点个数，start是错误的。