浅谈WQS二分

 本蒟蒻由于脑子笨，学wqs二分学了老长时间才搞懂，特此写篇文章加深印象。

  WQS二分本质上是一种带权二分，最早由大佬 王钦石 提出。其是一个用来解决如下问题的算法：

        有 n 个物品，需要从中选取 m 个，存在某种限制来计算选中物品的价值，求最大/小的价值。

使用这种技巧需要题目满足两个性质：

1. 设  表示从 n 个物品中选取 i 个的最优解，那么我们就可以得到点对 ，我们在图上画出所有  的点对，会发现其一定组成一个凸包(即凸函数) 。

2. 若题目中没有选取 m 个的限制，会十分容易地求得最优解。

我们先将性质1 的图像画出来：

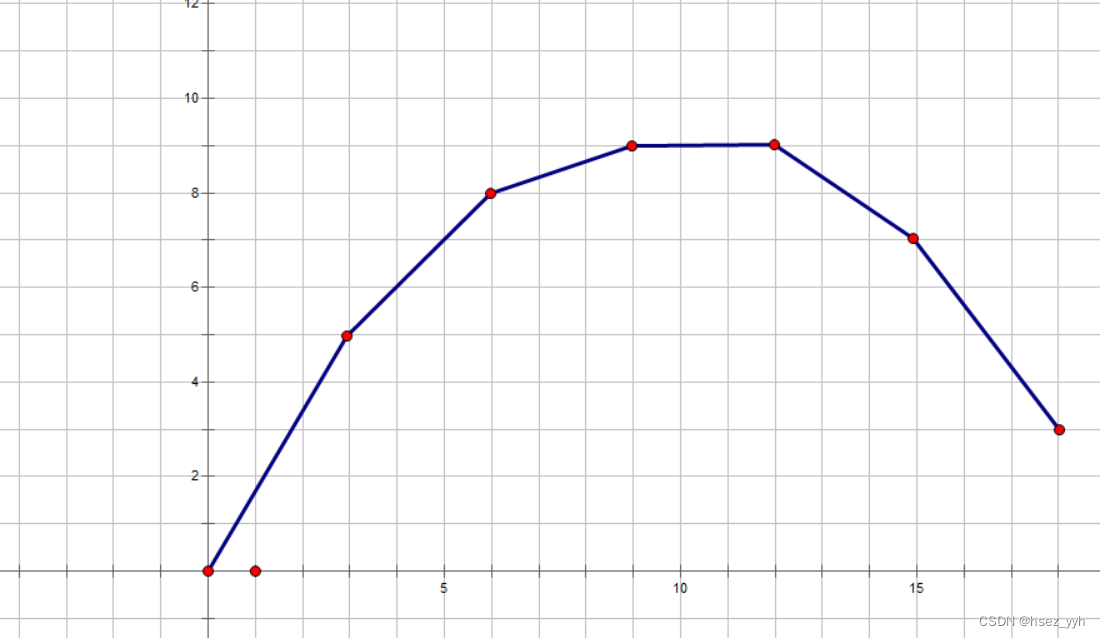
大概就长这样。此时我们用一条斜率为 k 的直线切这个凸包：

如上图，斜率为 k 的直线经过图中不同的点对时其纵截距也不同，但可以发现，该直线与凸包相切时纵截距最大。可以发现 ，假设直线与凸包相切于点 j ，则  。由于性质二，我们会很容易求出  的最大值，所以  的最大值 也会很容易求出。

  我们再试试用不同斜率的直线去切凸包：

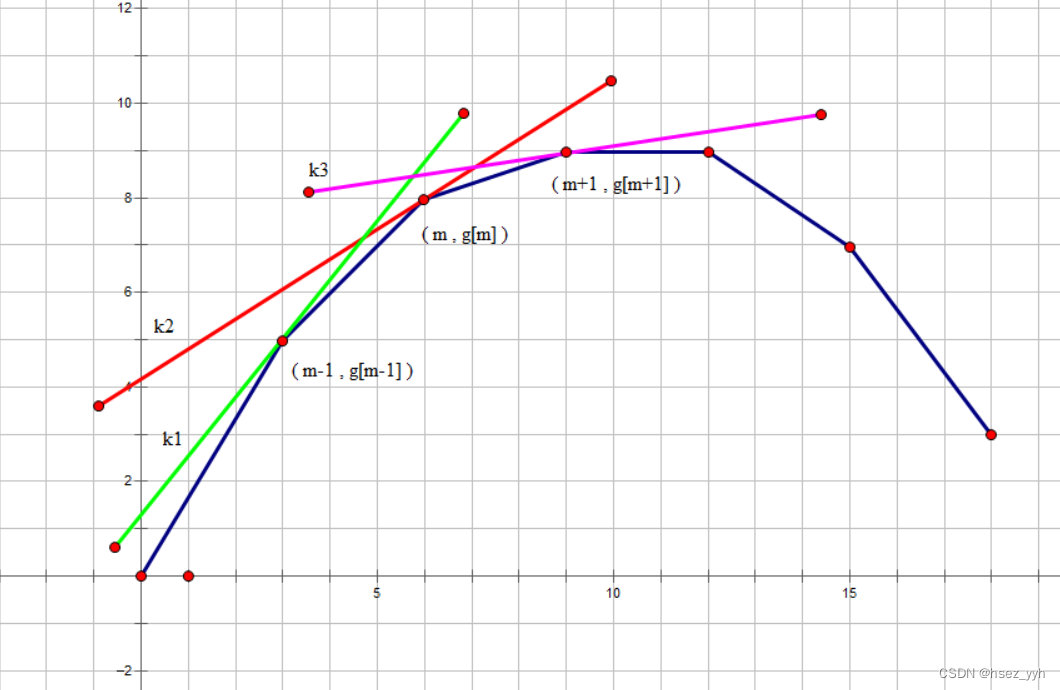
 显然可以发现随着斜率 k 的单调递减所得到的切点的横坐标单调递增，而上图 k=k2 时，所得到的切点为  ，也就是我们想要得到的答案，此时有  。因为  是容易求的，所以我们只需要简化变换斜率的过程，又由于满足单调性，我们自然而然地想到二分。

        具体过程如下：二分斜率，假设当前斜率为 mid ，将 mid 带入凸包求出当前的  ，判断切点于 m 的关系，如果切点在 m 的左侧，则说明斜率大了，那么缩小二分上界；如果切点在 m 的右侧，则说明斜率小了，增大二分的下界即可。

        还是来看一道例题辅助理解：洛谷P1484 种树 

        题目大意就是一共有 n 个位置，每个位置上种树会有不同的价值，最多种 k 棵树且相邻的位置只能种一棵树，求最大价值。

        读完题目发现，这就是个 wqs二分 的板子 。首先答案一定是关于 k 的凸函数，考虑如何证明： 设当前答案为  ，考虑 m+1 时的答案，分为两种情况：1. 会改变 m 时的选取情况，我们将选或不选的情况用 01 串来表示，那么只有可能将一个类似 01010 的串改成 10101 的串，显然这样的改变的增量会越来越小， 即   。 2. 不会改变 m 时的选取情况，即选一个全新的位置，那么该位置的价值显然小于 m 时选取的价值，所以依旧满足  。综合1，2 两种情况，发现斜率会越来越小，即组成一个上凸包。

        再来看看是否满足性质2 ，假设没有 k 的限制，那么设  表示选到第 i 个位置，第 i 个位置选(1) 或 不选(0) 时的最大价值，答案即为   。可以发现可以  求解，满足快速求得答案的性质，所以直接上 wqs二分 即可，具体实现看代码：

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N=5e5+10;
int n,m;
int a[N],mx,cnt,g[2][2];
LL dp[2][2],ans;
void solve(int xx)
{
	dp[0][1]=dp[0][0]=0; // 滚动数组求取最优解 
	g[0][1]=g[0][0]=0; // 记录当前最优解是选取几个位置 
	int s=0;
	for(int i=1;i<=n;i++,s^=1)
	{
		if(dp[s][0]>dp[s][1]||(dp[s][0]==dp[s][1]&&g[s][0]<g[s][1]))
			dp[s^1][0]=dp[s][0],g[s^1][0]=g[s][0];
		else dp[s^1][0]=dp[s][1],g[s^1][0]=g[s][1];
		dp[s^1][1]=dp[s][0]+(a[i]-xx);
		g[s^1][1]=g[s][0]+1;
	}
	if(dp[s][0]>dp[s][1]||(dp[s][0]==dp[s][1]&&g[s][0]<g[s][1]))
		ans=dp[s][0],cnt=g[s][0];
	else ans=dp[s][1],cnt=g[s][1];
}
LL res;
int main()
{
	scanf("%d %d",&n,&m);
	for(int i=1;i<=n;i++){
		scanf("%d",&a[i]);
		mx=max(mx,a[i]);
	}
	solve(0);
	if(cnt<=m) // 判断答案是否在 m 的限制前取到最优 
	{
		printf("%lld\n",ans);
		return 0;
	}
	// 如果答案被 m 限制，那么最优解只可能在 m 处取到  
	int l=0,r=mx;
	while(l<=r) // wqs二分，二分斜率 
	{
		int mid=(l+r)>>1;
		solve(mid);
		if(cnt<=m)
		{
			// 当前最优解在 m 的左侧，所以减小斜率 
			res=ans+(LL)mid*m;
			r=mid-1;
		}else l=mid+1; // 否则增大斜率 
	}
	printf("%lld\n",res);
	return 0;
}

        

        可以说实现还是非常容易的。

        下面再来看一道例题：洛谷P4983 忘情 

        题目大意是给定一个长度为 n 的正整数序列  ，将其分成 m 段，每段的价值为 ，使得每段价值之和最小，求最小值 。

        考虑没有 m 的限制，那么  表示当前分到 i 这个位置时价值之和的最小值，那么  。该方程转移显然是  的，考虑优化，将  展开后就会发现该式子可以斜率优化，所以复杂度将降为  。这样就满足快速求解的性质。

        在看看答案是否为 凸函数 ，由于   ，所以段数分的越多，答案会越优。又因为减小的值  ，每一次选择我们自然是选择最大的  ,所以随着分的段数的增加，每多分一段所减少的值也会越来越小，所以答案组成了一个 下凸包 。剩下的就是套 wqs二分 的板子了 。 代码如下：

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N=1e5+10;
int n,m;
LL a[N],s[N],res;
LL dp[N],ans,g[N];
int q[N],cnt,t[N];
void solve(LL xx)
{
	int hh=0,tt=-1;
	q[++tt]=0;
	for(int i=1;i<=n;i++)
	{
		while(hh<tt&&g[q[hh+1]]-g[q[hh]]<2LL*s[i]*(s[q[hh+1]]-s[q[hh]])) hh++;
		dp[i]=dp[q[hh]]+(s[i]-s[q[hh]]+1)*(s[i]-s[q[hh]]+1)+xx;
		t[i]=t[q[hh]]+1;
		g[i]=dp[i]+s[i]*s[i]-2LL*s[i];
		while(hh<tt&&(g[q[tt]]-g[q[tt-1]])*(s[i]-s[q[tt]])>=(g[i]-g[q[tt]])*(s[q[tt]]-s[q[tt-1]])) tt--;
		q[++tt]=i;
	}
	ans=dp[n];
	cnt=t[n];
}
int main()
{
	scanf("%d %d",&n,&m);
	for(int i=1;i<=n;i++)
	{
		scanf("%lld",&a[i]);
		s[i]=s[i-1]+a[i];
	}
	LL l=0,r=1e18;
	while(l<=r)
	{
		LL mid=(l+r)>>1;
		solve(mid);
		if(cnt<=m)
		{
			res=ans-m*mid;
			r=mid-1;
		}else l=mid+1;
	}
	printf("%lld\n",res);
	return 0;
}