本文详细介绍了多个涉及循环结构的编程题目，包括求余数、求乘积末尾的0、进位的三位数、找零钱、特殊回文数、完全平方数个数等，涵盖了数论、数位操作、完全平方数、回文数等多个知识点，旨在帮助读者熟练掌握循环结构的运用。
循环结构
前言
本章主要记录循环结构的算法练习，顺序结构可以查看上一篇文章，算法-顺序结构
1、求余数
1.描述
输入一个
正整数n
输出
输出余数
输入样例 1
1
输出样例 1
6
2.分析
本题最直接的方法就是先取余数再求和最后再取余数，切记不可先全部求和再取余数，因为这样会超时，也会超过整型范围。
当然还有一种方法，我们发现这个式子是有规律的，所以就可以打表记录每一次的余数，看看是否有规律。我们就可以先看前40个余数
res = []
t = 0
for i in range(1, 40):
t += 6 ** i
mod = t % 7
res.append(mod)
print(res)
[6, 0, 6, 0, 6, 0, 6, 0, 6, 0, 6, 0, 6, 0, 6, 0, 6, 0, 6, 0, 6, 0, 6, 0, 6, 0, 6, 0, 6, 0, 6, 0, 6, 0, 6, 0, 6, 0, 6]
我发现奇数位余数为6，偶数位余数为0，所以我们只需要判断数的奇偶性就可以直接的出答案
3.代码
方法一：
#include <iostream>
using namespace std;
int main(){
int n,i,ans=0,s=1;
cin>>n;
for(i=1;i<=n;i++){
s=s*6%7;
ans=(ans+s)%7;
}
cout<<ans;
}
方法二：
n=int(input())
x=n%2
if x==0:
print(0)
else:
print(6)
2、求余数（2）
1.描述
求1+11+111+1111+…+11….11（n个1）的和除以7的余数是多少？
输入
一行：一个正整数n
输出
一行：所得的余数
输入样例 1
1
输出样例 1
1
2.分析
这个题也是一样的，可以打表找到规律，也可以先求余数在求和再求余数
3.代码
方法一：
python
通过打表发现余数为42个为一组，这个可能不太好发现
a = []
s = 0
for i in range(1, 86):
s += int(str('1') * i)
a.append(s % 7)
print(a)
[1, 5, 4, 2, 4, 4, 5, 2, 1, 6, 1, 1, 2, 6, 5, 3, 5, 5, 6, 3, 2, 0, 2, 2, 3, 0, 6, 4, 6, 6, 0, 4, 3, 1, 3, 3, 4, 1, 0, 5, 0, 0, 1, 5, 4, 2, 4, 4, 5, 2, 1, 6, 1, 1, 2, 6, 5, 3, 5, 5, 6, 3, 2, 0, 2, 2, 3, 0, 6, 4, 6, 6, 0, 4, 3, 1, 3, 3, 4, 1, 0, 5, 0, 0, 1]
还有就是要注意数组的下标
a = []
s = 0
for i in range(1,43):
s += int(str('1')*i)
a.append(s%7)
n = int(input())
x = n % 42
print(a[x-1])
方法二：
c语言
#include <stdio.h>
int main(){
int s=0,k=0,n;
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
k=k*10+1;
k=k%7;
s=s+k;
}
printf("%d\n",s%7);
return 0;
}
3、乘积末尾的0
1.描述
输入一个正整数n；求n!=123*…*n，的乘积结果末尾有多少个0？
输入
输入一个正整数n。（n<=10000000）
输出
输出一行，表示乘积结果末尾是0的个数
输入样例 1
10
输出样例 1
2
2.分析
这个题就是数论里面的基本题，这里大家有兴趣可以去搜索一下证明过程
3.代码
n = int(input())
c=0
while(n):
c+=n//5
n//=5
print(c)
4、进位的三位数
1.描述
输入一个三位数a，求有多少个三位数与a的和发生进位的个数。
输入
输入一个三位数
输出
输出发生进位的三位数个数
输入样例 1
999
输出样例 1
900
2.分析
发生进位就是两个数字加起来大于10，也就是我们把这个三位数每一位都分离开来，然后进行判断，这里的话直接用python里面的map（）函数。
3.代码
n = int(input())
a,b,c=map(int,str(n))
q=0
for i in range(100,1000):
x,y,z=map(int, str(i))
if z+c>=10 or y+b>=10 or x+a>=10:
q+=1
print(q)
4、字母的值
1.描述
A、B、C各代表不同的数字，要使下面的等式成立：
AAA +BBB + CCC=CBBC
输出满足条件的A、B、C
输入
无
输出
输出A、B、C三个数，数与数之间用空格分开
输入样例 1
无
输出样例 1
1 1 1（输出样例）
2.分析
这里的话直接开三个循环，利用python里面的字符型和整型之间的转换快速完成判断
3.代码
for i in range(1, 9):
for j in range(1, 9):
for k in range(1, 9):
a = str(i) * 3
b = str(j) * 3
c = str(k) * 3
if int(a) + int(b) + int(c) == int(str(k) + str(j) * 2 + str(k)):
print("{} {} {}".format(i, j, k))
8 2 1
5、敲七
1.描述
输入一个正整数n，输出1~n中，含7和7的倍数的个数，还有包含7的数字例如（17，27，37…70，71，72，73…）
输入
输入正整数n：1<=n<=10000000
输出
输出一个正整数（即含7或7的倍数的个数）
2.分析
这里直接把每个数字分离开来看是否含有7，另外单独判断7的倍数，这里考察的就是数位分离的基本
3.代码
n = int(input()) # 输入
ans = 0
for i in range(1, n + 1):
j = i
if i % 7 == 0:
ans += 1
continue
while j > 0: # 数字分离
if j % 10 == 7: # 判断
ans += 1
break
j //= 10
print(ans)
6、特殊回文数
1.描述
123321是一个非常特殊的数，它从左边读和从右边读是一样的。
输入一个正整数n， 编程求所有这样的五位和六位十进制数，满足各位数字之和等于n。
输入
输入一行，包含一个正整数n。
输出
输出满足条件的回文整数的个数。
输入样例 1
52
输出样例 1
3
2.分析
思路也是一样的把数的每一位分离开来，先判断是否是回文数，再求合，判断。这里题目明确了5位和6位的数，所以这里可以借用python的map（）函数。也可用除的形式来保留每一位。
3.代码
python:
n = int(input())
count = 0
for i in range(10000, 100000):
if str(i) == str(i)[::-1]:
a, b, c, d, e = map(int, str(i))
if a + b + c + d + e == n:
count += 1
for j in range(100000, 1000000):
if str(j) == str(j)[::-1]:
a, b, c, d, e, f = map(int, str(j))
if a + b + c + d + e + f == n:
count += 1
print(count)
44
22
c++:
#include <iostream>
using namespace std;
int main(){
int n, ans=0,a,b,c;
ans=0;
cin>>n;
for(int i=100;i<1000;i++){
a=i/100;b=i%100/10;c=i%10;
if((a+b+c)*2==n) ans++;
}
for(int i=10;i<100;i++){
for(int j=0;j<10;j++){
a=i/10;b=i%10;
if((2*(a+b)+j)==n) ans++;
}
}
cout<<ans<<endl;
}
7、完全平方数个数
1.描述
输入整数n；求在1~n的整数中，使得：2020+7*n为完全平方数。求所有完全平方数的个数。
输入
一个正整数：n（1<n<=1000000）
输出
输出满足条件的完全平方数的个数
输入样例 1
100
输出样例 1
2
2.分析
这里主要是判断完全平方数，这里用到的一个技巧就是用int（）对sqrt（）函数返回的值取整，然后再对取整的值进行平方运算看是否等于原来的数值，当然，python里面**表示多少次方，后面乘以0.5就是开方，2就是平方。
3.代码
python 法一：
import math
n = int(input())
ans = 0
for i in range(1, n + 1):
x = 2020 + 7 * i
j = int(math.sqrt(x))
if j * j == x:
ans += 1
print(ans)
python 法二：
n = int(input())
ans = 0
for i in range(1, n + 1):
x = 2020 + 7 * i
if int(x ** 0.5) == x ** 0.5:
ans += 1
print(ans)
奈何python是解释性语言，速度太慢了，最后还是用c++过的，不过 这里主要是要明白思想
c++：
#include <cstdio>
#include <iostream>
#include<cmath>
using namespace std;
int main(){
int x,y,ans=0;
cin>>y;
for(int n=1;n<=y;n++){
x=2020+7*n;
int j=(int)sqrt(7*n+2020);
if(j*j==x)ans++;
}
cout<<ans<<endl;
return 0;
}
8、求六位数
1.描述
编程计算：六位数20□□08能被99整除，□□是多少？
输入
无
输出
输出一个两位数
输入样例 1
无
输出样例 1
11（样例）
提示
无
2.分析
这里和上面的题大同小异，两种思路，一是把中间两位看成1-100之间的数末尾和首都确定了，直接*100相加判断，二是字符串的拼接，
这里我给出字符串拼接的方式
3.代码
法一：
for i in range(1, 100):
s = 200008 + i * 100
if s % 99 == 0:
print(i)
break
法二：
for i in range(9):
for j in range(9):
if int('20'+str(i)+str(j)+'08')%99==0:
print("{}{}".format(i,j))
结果
71
9、-统计能被3、5整除不能被7整除的数字
1.描述
编程实现：在100内，能被3或5整除但不能被7整除的正整数的个数？
输入
无
输出
一个正整数表示统计结果
输入样例 1
无
输出样例 1
1（样例）
2.分析
这个直接判断就好，先找出能被3和5整除的放到列表里面，再删掉不能被7整除的
3.代码
x = []
for i in range(1, 100):
if i % 3 == 0 or i % 5 == 0:
x.append(i)
for j in x:
if j % 7 == 0:
x.remove(j)
print(len(x))
# 结果
40
10、数字串第30项
1.描述
下面是一串有规律的数
9，22，39，60，85，114，…
这串数中的第30个数是多少？
输入
无
输出
一个正整数
输入样例 1
无
输出样例 1
1（样例）
2.分析
这个不难看出就是一个等差数列
3.代码
s = 9
for i in range(29):
t = 13 + 4 * i
s += t
print(s)
# 结果
2010
11、k的最大值
1.描述
设a1、a2、…ak是k个互不相等的大于0的自然数，而且它们的和为2006，那么k的最大值是多少？
输入
无
输出
输出一个正整数
输入样例 1
无
输出样例 1
1（样例）
提示
无
2.分析
这里直接从第一项开始累加和，如果>=2006就把下标输出
3.代码
j, ans = 0, 0
for i in range(1, 2006):
ans += i
j = i
if ans >= 2006:
break
print(j - 1)
# 结果
62
12、找零钱
1.描述
书店里有一套漫画书共9册，第一册需24元，第二册需23元，第三册需22元，
以此类推，每册的售价都比它前面的一册要少一元，
如果哆啦A梦用200元去买这套漫画书，书店老板应该找他多少钱？
输入
无
输出
一个正整数
输入样例 1
无
输出样例 1
11（样例）
2.分析
一道中学数学题
3.代码
s = 0
for i in range(9):
s += 24-i
print(200-s)
# 结果
20
13、求满足条件五位数的最大最小值
1.描述
在一个互不相同数字的五位数中，统计能被3、7、11同时整除的整数个数，并输出最小值和最大值？
输入
无
输出
两个数，所求得的最小值和最大值，用空格分开
输入样例 1
无
输出样例 1
12345 23456（样例）
2.分析
根据题目要求挨个判断就可
3.代码
s = []
for i in range(10000, 100000):
a, b, c, d, e = map(int, str(i))
if a != b and b != c and c != d and d != e and a != c and a != d and a != e and b != d and b != e and c != e:
if i % 3 == 0 and i % 7 == 0 and i % 11 == 0:
s.append(i)
print('{} {}'.format(min(s), max(s)))
# 结果
10395 98637
14、末尾的数字
1.描述
在12 3… 100 的积中，从右边数有多少个0，和第 25 个数字是多少？
输入
无
输出
输出两个正整数：末尾是0的个数和从右到左第25个数字，用空格隔开
输入样例 1
无
输出样例 1
21 9（样例）
2.分析
这个题python可以直接求阶乘不用怕超范围，然后把数字放到数组里面
3.代码
import math
a = []
for i in str(math.factorial(100)):
a.append(int(i))
a = a[::-1]
n = a[24]
c = 0
for j in a:
if j == 0:
c += 1
else:
break
print(c, end=' ')
print(n)
# 结果
24 4
15、三角平方数
1.描述
称能够表示成1+2+3+…+k的形式的自然数为三角数。
有一个四位数N它既是三角数，又是完全平方数，则N的最小值是多少？
输入
无
输出
一个问题答案的正整数
输入样例 1
无
输出样例 1
123（样例）
2.分析
题目是四位数，所以我们大概可以确定发范围，k<=200，在进行累加判断是否是完全平方数
3.代码
s = 0
for i in range(1, 200):
s += i
if s < 1000:
continue
k = int(s ** 0.5)
if s == k * k:
break
print(s)
# 结果
1225
16、最小六位数
1.描述
在947后面添上三个不同的数字,
组成一个被2、3、5同时整除的最小的六位数,这个数是多少？
输入
无
输出
满足条件的最小的六位数
输入样例 1
无
输出样例 1
123456（样例）
2.分析
和上面的题的思路一样，字符串拼接
3.代码
for i in range(123, 1000):
a, b, c = map(int, str(i))
if a != b and a != c and b != c:
s = int('947' + str(i))
if s % 2 == 0 and s % 5 == 0 and s % 3 == 0:
print(s)
break
# 结果
947130
17、刘叔叔养的兔子
1.描述
刘叔叔养了400多只兔子，每3只兔子关在笼子里，那么最后一个笼子里有2只；如果每5只兔子关在一个笼子里，最后一个笼子有4只，如果7只兔子关在笼子里，最后一个笼子里有5只，问刘叔叔一共养了多少只兔子？
输入
无
输出
一个正整数：满足条件的最小值
输入样例 1
无
输出样例 1
400（样例）
2.分析
简单的判断
3.代码
for i in range(400, 500):
if i % 3 == 2 and i % 5 == 4 and i % 7 == 5:
print(i)
break
# 结果
404
18、数数小木块
1.描述
在墙角堆放着一堆完全相同的正方体小木块，如下图所示：
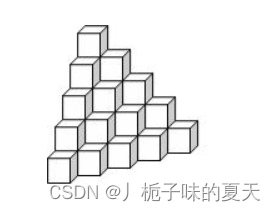
因为木块堆得实在是太有规律了，你只要知道它的层数就可以计算所有木块的数量了。
输入
只有一个整数 n ，表示这堆小木块的层数，已知1 <= n <= 1000 。
输出
只有一个整数，表示这堆小木块的总数量。
输入样例 1
5
输出样例 1
35
提示
无
2.分析
话不多说，简单的中学数学题
3.代码
n = int(input())
a=[]
x=1
for i in range(n):
x=x+i
a.append(x+i)
print(sum(a))
19、求a、b、c的值
1.描述
已知一个8位数 123ab45c能被792整除，求a，b，c的值？
输入
输入格式：无
输出
输出格式：
三个数字用空格隔开
输入样例 1
无
输出样例 1
1 1 1（样例）
2.分析
这样类型的题都可以直接字符串拼接解决
3.代码
for i in range(10):
for j in range(10):
for k in range(10):
s = int('123' + str(i) + str(j) + '45' + str(k))
if s % 792 == 0:
print('{} {} {}'.format(i, j, k))
# 结果
6 9 6
20、完全平方数个数2
1.描述
输入一个正整数n，求1~n中某个数m，m本身是完全平方数，其各个数值之和也是
完全平方数，输出满足这两个条件的正整数的个数。
输入
输入格式：一个正整数n
输出
输出格式： 输出满足条件的完全平方个数
输入样例 1
1
输出样例 1
1
2.分析
直接判断就好
3.代码
n = int(input())
ans = 0
for i in range(1, n + 1):
if int(i ** 0.5) == i ** 0.5:
x = [int(i) for i in str(i)]
s = sum(x)
if int(s ** 0.5) == s ** 0.5:
ans += 1
print(ans)
21、求不循环小数的个数
1.描述
输入两个正整数 n和m，求n/1,n/2,n/3,…,n/m中有多少个不是循环小数？
输入
输入格式：两个正整数n和m，用空格隔开
输出
输出格式 输出满足条件的个数
输入样例 1
2 2
输出样例 1
2
2.分析
这个题注意一个技巧，分子乘以10000000000对分母取余进行判断
3.代码
n, m = map(int, input().split())
ans = 0
for i in range(1, m + 1):
if n * 10000000000 % i == 0:
ans += 1
print(ans)
22、与7无关的数
1.描述
一个正整数,如果它能被7整除,或者它的十进制表示法中某一位上的数字为7,
则称其为与7相关的数.现求所有小于等于n(n < 100)的与7无关的正整数的平方和。
输入
输入为一行,正整数n
输出
输出
输出一行，包含一个整数，即小于等于n的所有与7无关的正整数的平方和。
输入样例 1
21
输出样例 1
2336
2.分析
这个题和第五题差不多，注意输出结果
3.代码
方法一：
n = int(input())
res = 0
def check(k): # 判断数字7
f = True
while k:
t = k % 10
if t == 7:
f = False
break
k //= 10
return f
for i in range(1, n + 1):
if i % 7 == 0 or not check(i):
continue
else:
res += i ** 2
print(res)
方法二：
n = int(input())
res = 0
for i in range(1, n + 1):
if i % 7 == 0 or 7 in [int(j) for j in str(i)]: # 这里利用list放每位数
continue
else:
res += i ** 2
print(res)
23、数字统计
1.描述
请统计某个给定范围[L, R]的所有整数中，数字2出现的次数。
比如给定范围[2, 22]，数字2在数2中出现了1次，在数12中出现1次，
在数20中出现1次，在数21中出现1次，在数22中出现2次，
所以数字2在该范围内一共出现了6次。
输入
输入共 1 行，为两个正整数 L 和 R，之间用一个空格隔开。
输出
输出共 1 行，表示数字 2 出现的次数。
输入样例 1
2 22
输出样例 1
6
输入样例 2
2 100
输出样例 2
20
提示
数据规模：
1<L<R<100000
2.分析
直接用python里面的count（）函数
3.代码
n,m=map(int,input().split())
c=0
for i in range(n,m+1):
c+=str(i).count('2')
print(c)
24、我家的门牌号
1.描述
我家住在一条短胡同里，这条胡同的门牌号从1开始顺序编号。若所有的门牌号之和减去我家门牌号的两倍，恰好等于n，
求我家的门牌号及总共有多少家。数据保证有唯一解。
样例输入
输入
输入
一个正整数n。
输出
输出
一行，包含两个正整数，分别是我家的门牌号及总共有多少家，中间用单个空格隔开。
输入样例 1
100
输出样例 1
10 15
提示
数据规模：
1<n < 100000
2.分析
这里注意逻辑，直接按照题目要求做就是了
3.代码
n = int(input())
for i in range(1, 100000):
f = True # 循环终止的判断
temp = (1 + i) * i // 2 # 看作等差数列求和
for j in range(1, n + 1):
if temp - j * 2 == n: # 判断是否符合要求
print(f'{j} {i}')
f = False
break
if f == False:
break
25、寻找完全数
1.描述
一个数如果恰好等于它的真因子之和，这个数就称为“完全数”。
例如6=1＋2＋3。编程找出N以内的所有完全数。1没有真因子，
因此1不是完全数。编程实现求取2~n之间的完全数的个数
输入
一个整数N。
输出
一个正整数，即所求的完全数个数
输入样例 1
10
输出样例 1
1
2.分析
基础题直接上代码
3.代码
n = int(input())
res = 0
for i in range(2, n + 1):
ans = 0 # 统计因子的和
for j in range(2, i // 2 + 1): # 求因子
if i % j == 0:
ans += j
if ans + 1 == i:
res += 1
print(res)
26、求数根
1.描述
数根可以通过把一个数的各个位上的数字加起来得到。如果得到的数是一位数，
那么这个数就是数根。如果结果是两位数或者包括更多位的数字，那么再把这些数字加起来。
如此进行下去，直到得到是一位数为止。
比如，对于24来说，把2和4相加得到6，由于6是一位数，因此6是24的数根。再比如39，
把3和9加起来得到12，由于12不是一位数，因此还得把1和2加起来，最后得到3，
这是一个一位数，因此3是39的数根。
输入
一个正整数n。
输出
两个正整数，分别表示输入数字的数根和转换为树根的次数，之间用一个空格隔开。
输入样例 1
24
输出样例 1
6 1
提示
数据规模：
1<n<10000000
2.分析
这道题用字符串会更好做一点
3.代码
n = int(input()) # 输入
ans = 0 # 记录转换次数
while True:
s = str(n) # 转为字符串
if len(s) == 1: # 循环终止条件，只有一个数字
res = int(s) # 转为整型并记录
break
x = [int(i) for i in s] # 数字每一位分解放到列表里面
n = sum(x) # 求和
ans += 1 # 次数加一
print(f'{res} {ans}')
27、A钱买A鸡
1.描述
“A钱买A鸡”的问题：3文钱可以买1只公鸡，2文钱可以买1只母鸡，
1文钱可以买3只小鸡，要用A文钱买A只鸡，请输出总的方案数。
输入
一个正整数A。
输出
一个正整数，表示用A文钱买A只鸡的总的方案数。
输入样例 1
100
输出样例 1
6
2.分析
注意直接三个循环可能会超时
3.代码
a = int(input())
res = 0 # 记录方案数
for i in range(a // 3 + 1):
for j in range(a // 2 + 1):
k = a - j - i # 减少循环次数
if k % 3 != 0:
continue
if i * 3 + j * 2 + k // 3 == a :
res += 1
print(res)
总结
以上就是一些基本的循环结构的题，主要还是熟悉一些基本的语法，题目相对都是入门题。欢迎大家留言交流。下一篇 算法训练-循环模拟
扫一扫
575
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
