ACM-ICPC 2018 沈阳赛区网络预赛 G. Spare Tire（容斥）

题目链接：https://nanti.jisuanke.com/t/31448

样例输入 
4 4
样例输出 
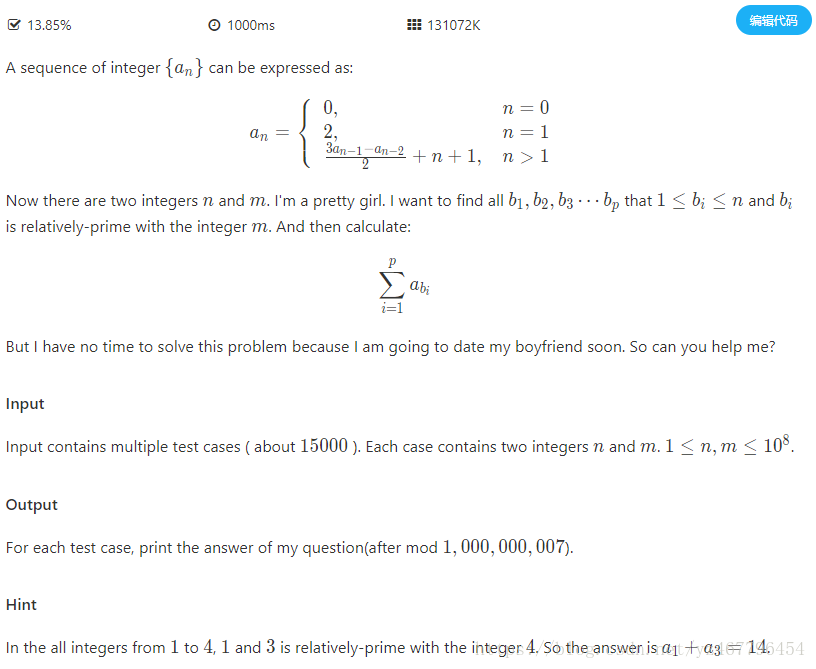
14

题意：给出a的递推式，1到n中与m互质的数为i，求a[i]的和

思路：得到a的通项公式为,Sn的通项为,与m不互质的数，是取m的素因子的乘积，那么将m分解质因数，通过容斥原理，就可以得到与m不互质的数，总和减去这些数对应的a的和就是答案了。在求这些不互质数对应a的总和的时候，如果一个一个求会超时，需要直接求和。比如存在一个素因子是k，那么需要求下标为k，2k，3k，4k……的a的和，即求通项的求和，为，项数为n/k。

#include<queue>
#include<cstring>
#include<string>
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<set>
using namespace std;
typedef long long ll;
const int maxn=100000;
const int mod=1e9+7;
ll mo(ll a,ll pp){
    if(a>=0&&a<pp)return a;
    a%=pp;
    if(a<0)a+=pp;
    return a;
}
ll powmod(ll a,ll b,ll pp){
    ll ans=1;
    for(;b;b>>=1,a=mo(a*a,pp)){
        if(b&1)ans=mo(ans*a,pp);
    }
    return ans;
}

ll inv1(ll b){
	return powmod(b,mod-2,mod);
}
bool check[maxn+7];
int phi[maxn+7];
int prime[maxn+7];
int tot;
void phi_and_prime_table(int N) {
    memset(check,false,sizeof(check));
    phi[1]=1;
    tot=0;
    for(int i=2; i<=N; i++) {
        if(!check[i]) {
            prime[tot++]=i;
            phi[i]=i-1;
        }
        for(int j=0; j<tot; j++) {
            if(i*prime[j]>N)break;
            check[i*prime[j]]=true;
            if(i%prime[j]==0) {
                phi[i*prime[j]]=phi[i]*prime[j];
                break;
            }
			else{
                phi[i*prime[j]]=phi[i]*(prime[j]-1);
            }
        }
    }
}
int p[107],dex[107];
int getFactors(ll x) {//分解质因数 
    int fatcnt=0;
    ll tmp=x;
    for(int i=0; prime[i]<=tmp/prime[i]; i++) {
        dex[fatcnt]=0;
        if(tmp%prime[i]==0) {
            p[fatcnt]=prime[i];
            while(tmp%prime[i]==0) {
                dex[fatcnt]++;
                tmp/=prime[i];
            }
            fatcnt++;
        }
    }
    if(tmp!=1) {
        p[fatcnt]=tmp;
        dex[fatcnt++]=1;
    }
    return fatcnt;
}
ll N;
ll S(ll x){
	ll n=N/x;
	ll sum=(n*(n+1)%mod*(2*n+1)%mod)*inv1(6)%mod*x%mod*x%mod+n*(n+1)%mod*inv1(2)%mod*x%mod;
	sum%=mod;
	return sum;
}
int main() {
    phi_and_prime_table(maxn);
	ll m;
    while(~scanf("%lld%lld",&N,&m)){
		int num=getFactors(m);//素因子个数 
		ll sum=S(1);
		ll s=0;
		for(int state=1;state<(1<<num);state++){//遍历所有状态 
			int tmp=1;
			int cnt=0;
			for(int i=0;i<num;i++){
				if(state&(1<<i)){
					cnt++;
					tmp*=p[i];
				}
			}
			if(cnt&1){//容斥 
				s=(s+S(tmp))%mod;
			}
			else{
				s=(s-S(tmp)+mod)%mod;
			}
		
		}
		sum=(sum+mod-s)%mod;
		printf("%lld\n",sum);
	}
    return 0;
}