每日一题.切棍子的最小成本；动态规划的运用-CSDN博客

本文链接：https://blog.csdn.net/yzxyy_zzb/article/details/143692559

本题出自LeetCode1547每日一题切棍子的最小成本，今天双十一，倒是剁起了棍子，虽然说标签是困难，但这道题肯定是没那么难的，因为很快就发现这是一道标准的动态规划或者用递归做

题目

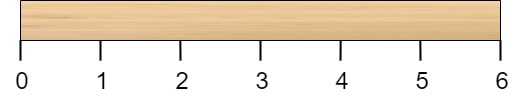
有一根长度为 n 个单位的木棍，棍上从 0 到 n 标记了若干位置。例如，长度为 6 的棍子可以标记如下：

给你一个整数数组 cuts ，其中 cuts[i] 表示你需要将棍子切开的位置。

你可以按顺序完成切割，也可以根据需要更改切割的顺序。

每次切割的成本都是当前要切割的棍子的长度，切棍子的总成本是历次切割成本的总和。对棍子进行切割将会把一根木棍分成两根较小的木棍（这两根木棍的长度和就是切割前木棍的长度）。请参阅第一个示例以获得更直观的解释。

返回切棍子的 最小总成本 。

示例 1：
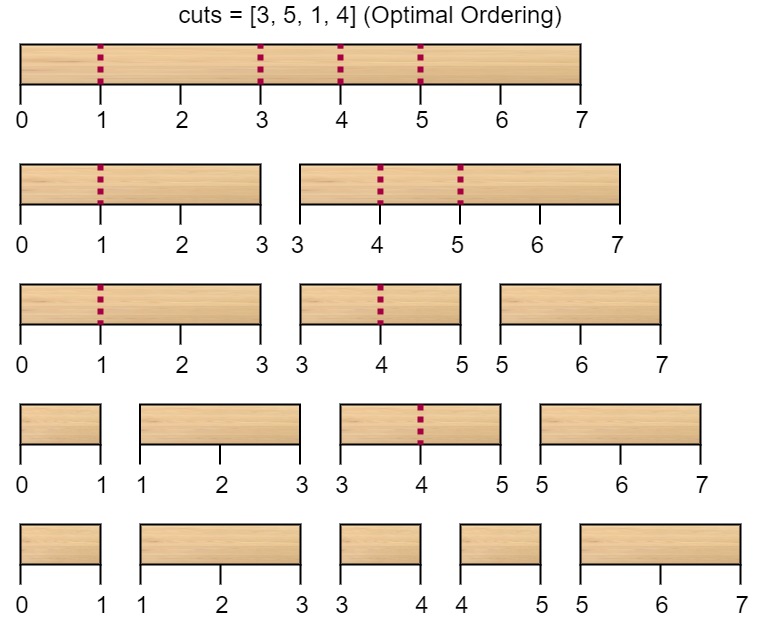
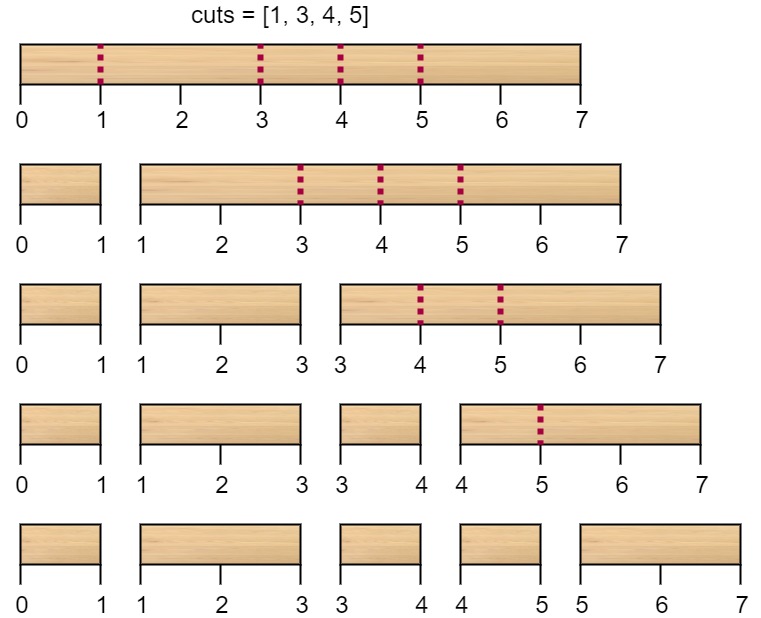
输入：n = 7, cuts = [1,3,4,5]
输出：16
解释：按 [1, 3, 4, 5] 的顺序切割的情况如下所示：
第一次切割长度为 7 的棍子，成本为 7 。第二次切割长度为 6 的棍子（即第一次切割得到的第二根棍子），第三次切割为长度 4 的棍子，最后切割长度为 3 的棍子。总成本为 7 + 6 + 4 + 3 = 20 。
而将切割顺序重新排列为 [3, 5, 1, 4] 后，总成本 = 16（如示例图中 7 + 4 + 3 + 2 = 16）。
示例 2：
输入：n = 9, cuts = [5,6,1,4,2]
输出：22
解释：如果按给定的顺序切割，则总成本为 25 。总成本 <= 25 的切割顺序很多，例如，[4, 6, 5, 2, 1] 的总成本 = 22，是所有可能方案中成本最小的。
提示：

2 <= n <= 10^6
1 <= cuts.length <= min(n - 1, 100)
1 <= cuts[i] <= n - 1
cuts 数组中的所有整数都 互不相同

解题思路

问题背景

想象你有一根很长的木棍，你需要在某些特定的位置将它切成几段。每次切割的成本等于你要切割的那部分木棍的长度。你的目标是以最低的成本完成所有切割。

解决方案

为了找到最低的成本，我们需要考虑的是如何选择切割的顺序。但是直接考虑所有可能的切割顺序是非常复杂的，所以我们采用了一种叫做“动态规划”的方法来简化问题。

动态规划的基本思想

状态定义：我们用 f[i][j] 来表示从第 i 个切割点到第 j 个切割点之间（包括这两个点）完成所有切割所需的最小成本。
状态转移：假设我们在 i 到 j 之间的某个点 k 做了第一次切割，那么这次切割会将木棍分成两部分，左边是从 i 到 k-1，右边是从 k+1 到 j。这时，我们的问题就被分解成了两个小一点的问题：计算左边部分的最小成本 f[i][k-1] 和右边部分的最小成本 f[k+1][j]。而这次切割的成本是整个未切割前的木棍长度，即 cuts[j+1] - cuts[i-1]。
选择最优解：我们需要在所有可能的第一次切割点 k 中选择一个使得 f[i][k-1] + f[k+1][j] + (cuts[j+1] - cuts[i-1]) 最小的方案。

边界条件

如果 i > j，这意味着没有需要切割的部分，所以成本为 0。

计算过程

初始化：首先将所有的 f[i][j] 初始化为无穷大，除了那些 i > j 的情况，它们的成本为 0。
填充表：按照从小到大的顺序计算每个 f[i][j] 的值。对于每一个 i 和 j，尝试所有可能的 k 来更新 f[i][j] 的值。
最终答案：f[1][m] 就是我们要找的最小总成本，其中 m 是所有切割点的数量。

例子

假设你有木棍长度为 n=7，切割点为 [1, 3, 4, 5]。经过排序后，切割点加上两端点变为 [0, 1, 3, 4, 5, 7]。通过上述方法计算，你可以找到将这根木棍完全切开所需的最小成本。

题解

Java

import java.util.ArrayList;
import java.util.Collections;

class Solution {
    public int minCost(int n, int[] cuts) {
        // 第一步：将0和n加入作为区间边界
        ArrayList<Integer> list = new ArrayList<>();
        list.add(0);
        list.add(n);
        for (int num : cuts) {
            list.add(num);
        }
        Collections.sort(list);

        // 第二步：创建dp数组
        int m = list.size();
        int[][] dp = new int[m][m];

        // 从后往前遍历i
        for (int i = m - 1; i >= 0; --i) {
            // 从前往后遍历j，且j至少比i大2
            for (int j = i + 2; j < m; ++j) {
                // 初始化dp[i][j]为最大值
                dp[i][j] = Integer.MAX_VALUE;

                // 枚举分割点k
                for (int k = i + 1; k < j; k++) {
                    // 更新dp[i][j]的最小值
                    dp[i][j] = Math.min(dp[i][j], 
                        dp[i][k] + dp[k][j] + list.get(j) - list.get(i));
                }
            }
        }

        // 返回从0到m-1的最小成本
        return dp[0][m - 1];
    }
}

思路

初始化列表：

将0和n加入到一个列表中，表示木棍的两端。
将所有的切割点加入到列表中。
对列表进行排序，确保切割点按顺序排列。

创建DP数组：

创建一个二维数组 dp，大小为 m x m，其中 m 是列表的长度。
dp[i][j] 表示从第 i 个切割点到第 j 个切割点之间的最小切割成本。

填充DP数组：

从后往前遍历 i，确保子问题先于大问题被解决。
从前往后遍历 j，且 j 至少比 i 大2，确保中间有至少一个切割点。
初始化 dp[i][j] 为最大值 Integer.MAX_VALUE。
枚举中间的切割点 k，计算并更新 dp[i][j] 的最小值。

返回结果：

最终返回 dp[0][m-1]，即从0到n的最小切割成本。

关键点

排序：确保切割点按顺序排列，方便后续处理。
动态规划：通过子问题的最优解来构建大问题的最优解。
状态转移方程：dp[i][j] = Math.min(dp[i][j], dp[i][k] + dp[k][j] + list.get(j) - list.get(i))，其中 list.get(j) - list.get(i) 表示当前切割的成本。