分布类相关的可视化图像-CSDN博客

import matplotlib.pyplot as plt
import numpy as np
data = np.random.randn(1000)
plt.hist(data, bins=30, edgecolor='black', alpha=0.7)
plt.title('Histogram')
plt.xlabel('Value')
plt.ylabel('Frequency')
plt.show()

结果

生成一个直方图，横轴表示数据值的区间，纵轴表示每个区间内的频数，通过直方图可以直观地看到数据集中在中间区域，符合正态分布的特征。

2. 密度图（Density Plot）

特点

平滑的分布曲线：通过核密度估计（KDE）将数据的分布平滑化，展示数据的概率密度函数。
更灵活：相比于直方图，密度图不受bin数量的影响，能够更平滑地展示数据分布。
可叠加：可以将多个数据集的密度图叠加在一起，便于比较不同数据集的分布差异。

应用场景

多组数据比较：比较不同组数据的分布形状，判断它们是否来自同一分布。
金融数据分析：分析资产收益率的分布，判断其风险特征。
生物医学：分析基因表达数据的分布。

Python实现

import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np

data1 = np.random.randn(1000)
data2 = np.random.randn(1000) + 2
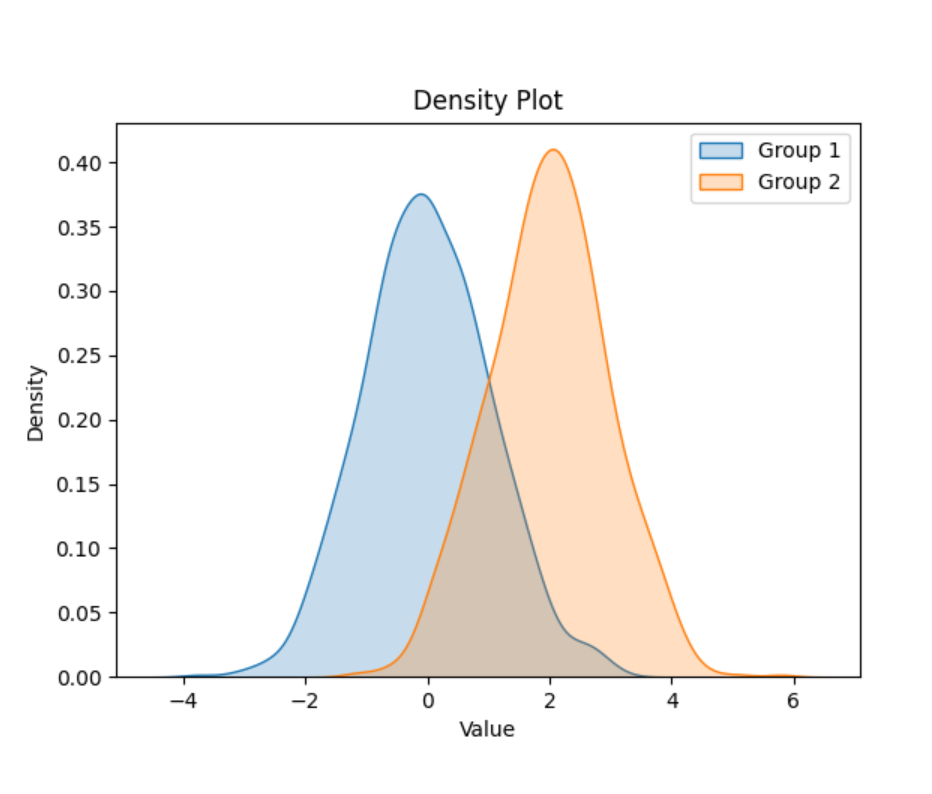
sns.kdeplot(data1, label='Group 1', fill=True)
sns.kdeplot(data2, label='Group 2', fill=True)

plt.title('Density Plot')
plt.xlabel('Value')
plt.ylabel('Density')
plt.legend()
plt.show()

结果

生成两个数据集的密度图，通过曲线的形状可以直观地看出两个数据集的分布差异，例如Group 1的分布更接近标准正态分布，而Group 2整体偏移了2个单位。

3. 箱线图（Box Plot）

特点

五数概括：通过展示数据的最小值、第一四分位数（Q1）、中位数（Q2）、第三四分位数（Q3）和最大值，提供数据的统计概览。
异常值检测：能够直观地识别出数据中的异常值（通常定义为超出1.5倍四分位距范围的点）。
简洁明了：用较少的图形元素展示较多的统计信息。

应用场景

数据质量分析：快速识别数据中的异常值和数据的集中趋势。
多组数据比较：比较不同组数据的分布范围和离散程度。
教育评估：分析学生成绩分布，判断成绩的集中趋势和离散程度。

Python实现

import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
np.random.seed(42)
data_group1 = np.random.normal(0, 1, 100)
data_group2 = np.random.normal(2, 1.5, 100)
data_group3 = np.random.normal(-1, 0.8, 100)
all_data = [data_group1, data_group2, data_group3]
labels = ['Group 1', 'Group 2', 'Group 3']
plt.figure(figsize=(8, 5))
plt.boxplot(all_data, labels=labels, patch_artist=True)
plt.title("Basic Box Plot (Matplotlib)")
plt.ylabel("Value")
plt.grid(axis='y', linestyle='--', alpha=0.7)
plt.show()
plt.figure(figsize=(8, 5))
sns.boxplot(data=all_data)  # 或使用DataFrame长格式数据
plt.xticks(ticks=[0, 1, 2], labels=labels)
plt.title("Basic Box Plot (Seaborn)")
plt.ylabel("Value")
plt.show()

结果

生成一个箱线图，横轴为分组标签，箱体显示Q1-Q3，中线为中位数，须线延伸至非异常值范围，异常值以圆圈标记。

4. 小提琴图（Violin Plot）

特点

结合箱线图和密度图：在箱线图的基础上，两侧添加了密度图的形状，展示了数据的分布密度。
更丰富的信息：不仅能够展示数据的统计特征，还能通过密度形状直观地看出数据的分布形态。
美观且信息量大：在有限的空间内展示更多的信息，适合用于展示复杂数据集的分布。

应用场景

多组数据比较：比较不同组数据的分布形态和统计特征。
生物医学研究：分析不同实验组的基因表达数据分布。
社会科学研究：比较不同人群的收入分布等。

Python实现

import seaborn as sns
import matplotlib.pyplot as plt
import numpy as np
data1 = np.random.randn(1000)
data2 = np.random.randn(1000) + 2
sns.violinplot(data=[data1, data2])
plt.title('Violin Plot')
plt.xticks([0, 1], ['Group 1', 'Group 2'])
plt.ylabel('Value')
plt.show()

结果

生成一个小提琴图，中间的白色点表示中位数，箱子部分表示数据的中间50%范围，两侧的形状表示数据的密度分布。通过小提琴图可以直观地看出两个数据集的分布差异，例如Group 1的分布更集中，而Group 2的分布更分散且整体偏移了2个单位。

5.蜂巢图（Bee Swarm Plot）

特点

避免重叠：通过调整数据点的位置，避免了传统散点图中数据点重叠的问题，使得每个数据点都能清晰显示。
直观展示分布：能够直观地展示数据的分布情况，包括数据的集中区域、离散程度和异常值。
结合统计信息：可以与箱线图结合使用，同时展示数据的统计特征（如中位数、四分位数）和每个数据点的具体位置。

应用场景

生物医学研究：展示实验数据的分布情况，例如基因表达水平、药物反应强度等。
市场调研：分析用户评分、产品价格等数据的分布，判断数据的集中趋势和离散程度。
教育评估：展示学生成绩分布，分析成绩的集中区域和异常值。

Python实现

import seaborn as sns
import matplotlib.pyplot as plt
import numpy as np
data = np.random.randn(1000)
sns.stripplot(data=data, jitter=True, size=3, color="blue", edgecolor="gray")
plt.title('Bee Swarm Plot')
plt.xlabel('Group')
plt.ylabel('Value')
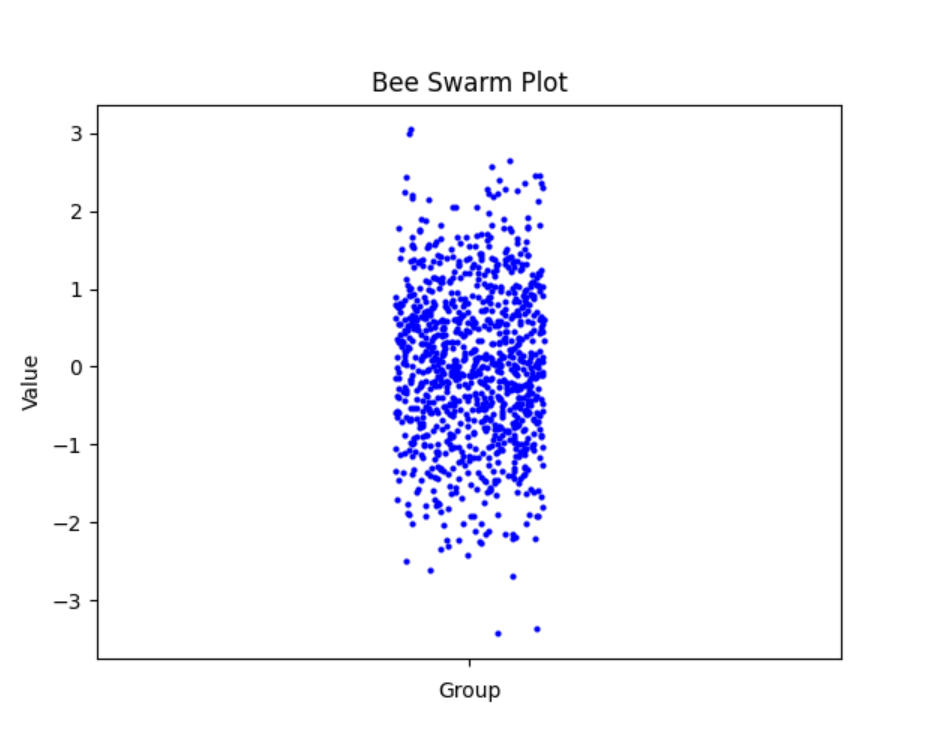
plt.show()