动态规划笔记

最新推荐文章于 2024-03-09 00:35:29 发布

z1185196212

最新推荐文章于 2024-03-09 00:35:29 发布

阅读量771

点赞数 1

分类专栏：数据结构与算法

本文链接：https://blog.csdn.net/z1185196212/article/details/52312194

版权

数据结构与算法专栏收录该内容

2 篇文章 0 订阅

订阅专栏

分治技术的问题

如果子问题不是相互独立的，分治将重复计算子问题，效率很低

动态规划的核心思想

把原始问题划分成一系列子问题
求解每个子问题仅一次，并将结果存入到一个表中，以后用到时直接取用，不重复计算，节省计算时间；自底向上进行计算，分治是自顶向上

使用动态规划的条件

最优子结构，使我们能自底向上完成问题。保证了动态规划的正确性
重叠子问题，在问题的求解过程中，很多子问题将被重复使用。如果没有重复子问题，使用动态规划就是在浪费存储空间，没有达到加速的效果。保证了动态规划的有效性

动态规划算法的设计步骤

分析优化解的结构
递归地定义最优解的代价
自底向上地计算优化解的代价保存之，并获取构造最优解的信息，保证每次计算时都用到之前计算过并存储起来的数据
根据构造最优解的信息构造优化解

几个栗子

1、设A1,A2,…,An为矩阵序列，Ai为Pi-1×Pi阶矩阵，i = 1,2,…,n. 确定乘法顺序使得元素相乘的总次数最少.
输入：向量P = <P0, P1, … , Pn>

实例：

P = <10, 100, 5, 50>  A1: 10 × 100, A2: 100 × 5, A3: 5 × 50

乘法次序：

(A1 A2)A3: 10 × 100 × 5 + 10 ×5 × 50 = 7500

        A1(A2 A3): 10 × 100 × 50 + 100 × 5 × 50 = 75000

分析：

记Ai,j=Ai*Ai+1*....*Aj

–cost(Ai,j )=计算Ai-j的代价

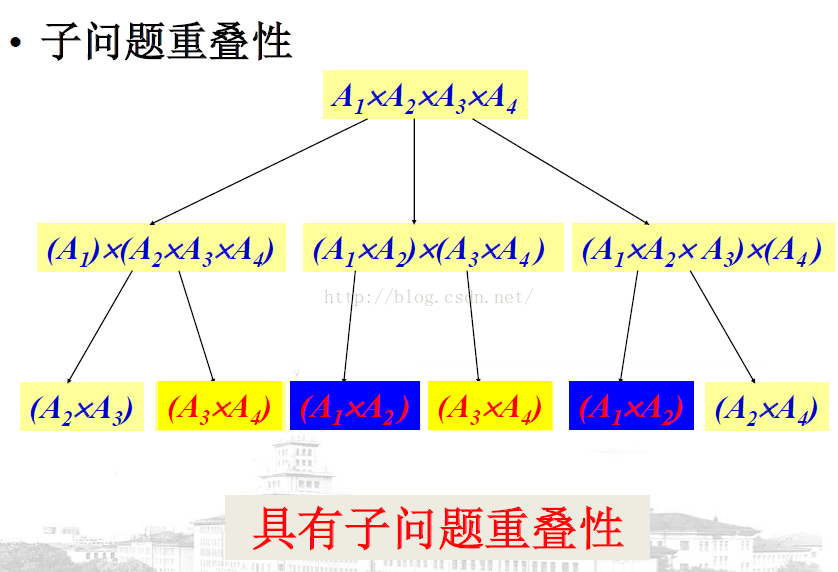
若计算Ai,j的优化顺序在k处断开，即Ai,j=Ai.k*Ak+1.j，则Ai.k和Ak+1为其分别所对应的子问题的最优解。即具有优化子结构。由下图分析可以知道具有子问题重叠性，所以可以用动态规划算法。

递推方程：

代码：

#include<stdio.h>
#define N 5
int m[N+1][N+1]; //m[i][j]存储Ai到Aj的最小乘法次数
int s[N+1][N+1];//s[i][j]存储Ai到Aj之间加括号的位置

void RecurMatrixChain(int P[],int n)
{
    int i,l,k,j;
    int q;
    for(i=1;i<=n;i++)
    {
        m[i][i]=0;        //只有一个矩阵
    }
    for(l=2;l<=n;l++)     //计算的l对角线
    {
        //计算m[i][j]
        for(i=1;i<=n-l+1;i++)
        {
            j=i+l-1;
            m[i][j]=999999;
            s[i][j]=i;
            //乘号打在k的后面的情况
            for(k=i;k<j;k++)
            {

                q=m[i][k]+m[k+1][j]+P[i-1]*P[k]*P[j];
                if(m[i][j]>q)
                {

                    m[i][j]=q;
                    s[i][j]=k;
                }
            }
        }
    }
}
int main()
{
    int P[N+1]={30,35,15,5,10,20};
    RecurMatrixChain(P,N);
    printf("%d %d",m[1][5],s[1][5]);
    return 0;
}<span style="font-size:14px;"><strong>
</strong></span>

2、最长公共子序列问题

问题描述：字符序列的子序列是指从给定字符序列中随意地（不一定连续）去掉若干个字符（可能一个也不去掉）后所形成的字符序列。令给定的字符序列X=“x0，x1，…，xm-1”，序列Y=“y0，y1，…，yk-1”是X的子序列，存在X的一个严格递增下标序列<i0，i1，…，ik-1>，使得对所有的j=0，1，…，k-1，有xij=yj。例如，X=“ABCBDAB”，Y=“BCDB”是X的一个子序列。

第i前缀
–设X=(x1, x2, ..., xn)是一个序列，X的第i前缀Xi是一个序列，定义为Xi=(x1, ..., xi )

设C[i,j]: 保存Xi与Yj的LCS的长度。

定理（优化子结构）设X=(x1, ..., xm)、Y=(y1, ..., yn) 是两个序列，Z=(z1, ..., zk)是X与Y的LCS，我们有：
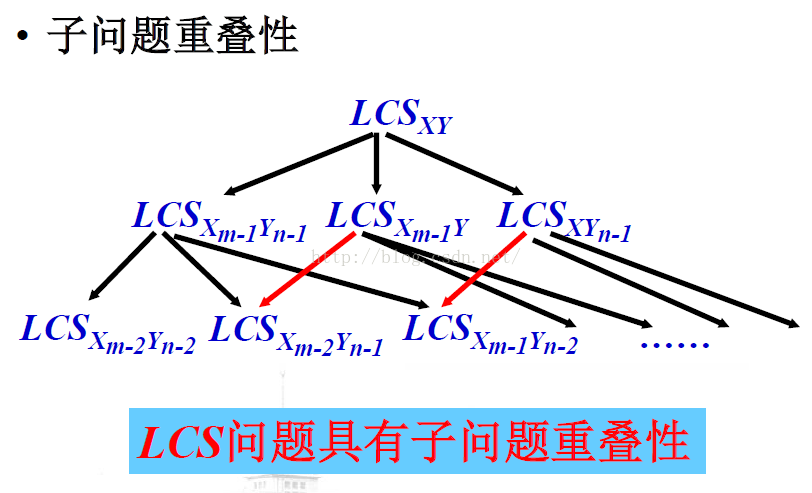
⑴ 如果xm=yn, 则zk=xm=yn, Zk-1是Xm-1和Yn-1的LCS，即，LCSXY = LCSXm-1Yn-1+ <xm=yn>.
⑵ 如果xm不等于yn，且zk不等于xm，则Z是Xm-1和Y的LCS，即 LCSXY= LCSXm-1Y
⑶ 如果xm不等于yn,且zk不等于yn,则Z是X与Yn-1的LCS，即 LCSXY= LCSXYn-1

数据结构：
C[m+1,n+1]: C[i,j]是Xi与Yj的LCS的长度
B[m+1,n+1]: B[i,j]是指针，指向计算C[i,j]时所选择的子问题的优化解所对应的C表的表项

#include<stdio.h>
#include <string.h>
#define MAXLEN 100

int b[MAXLEN+1][MAXLEN+1];
int c[MAXLEN+1][MAXLEN+1];

void LCSLength(char *x, char *y, int m, int n)
{
    int i,j;
    for(i=0;i<=m;i++)
    c[i][0]=0;
    for(j=0;j<=n;j++)
    c[0][j]=0;
    for(i=1;i<=m;i++)
    for(j=1;j<=n;j++)
    {
        if(i==j)
        {
            c[i][j]=c[i-1][j-1]+1;
            b[i][j]=0;                //记录方向
        }
        else if(c[i-1][j]>=c[i][j-1])
        {
            c[i][j]=c[i-1][j];
            b[i][j]=1;
        }
        else
        {
            c[i][j]=c[i][j-1];
            b[i][j]=-1;
        }
    }
}

void PrintLCS(char* x,int i,int j)
{
    if(i==0||j==0)
    return;
    if(b[i][j]==0)
    {
        PrintLCS(x,i-1,j-1);
        printf("%c",x[i]);         //注意这两句的顺序不能颠倒
    }
    else if(b[i][j]==1)
        PrintLCS(x,i-1,j);
    else
        PrintLCS(x,i,j-1);
}

int main()
{
    char x[MAXLEN] = {"ABCBDAB"};
    char y[MAXLEN] = {"BDC"};
    int m, n;

    m = strlen(x);
    n = strlen(y);

    LCSLength(x, y, m, n);
    PrintLCS(x, m, n);

    return 0;
}

三、优化子结构的分类

编号动态规划：输入为x1, x2, …, xn, 子问题是x1, x2, …,xi，子问题复杂性为O(n)(最大不下降子序列问题)
• 划分（区间）动态规划：输入为x1, x2, …, xn, 子问题为xi, xi+1,…, xj，子问题复杂性是O(n2) (矩阵链乘问题，凸多边形三角泡分)
• 数轴动态规划：输入为x1, x2, …, xn和数字C，子问题为x1, x2, …, xi, K(K≤C)，子问题复杂性O(nC) (0-1背包问题)
• 前缀动态规划：输入为x1, x2, …, xn和y1, y2, …, ym，子问题为x1, x2, …, xi和y1, y2, …, yj，子问题复杂性是O(mn) (最长公共子序列问题)

• 树形动态规划：输入是树，其子问题为子树，子问题复杂性是子树的个数。(树中独立集合问题)

1、最大不下降子序列问题

一般有两种表示状态的方法：
1) 状态i表示前i个元素构成的最优解，可能不包含第i个元素。
2) 状态i表示在必须包含第i个元素的情况下前i个元素构成的最优解。

• 输入: 一个数字序列 a[1..n]
• 子序列是数字序列的子集合，且和序列中数字顺序相同，即递增子序列是其中数字严格增大的子序列
• 输入: 具有最大长度的递增子序列.

算法分析：

• 优化子结构：假设最长递增子序列中包含元素ak，那么一定存在一组最优解，它包含了a1, a2, …, ak-1这个序列的最长递增子序列。
• 重叠子问题: ak和ak+1?
• 子问题的表示：令dp[i]表示以第i个元素结尾的前i个元素构成序列的最长递增子序列的长度。
• 最优解递归表达式：
dp[i] = max { dp[j] | 0 < j < i; aj < ai } + 1

代码：

private static int solve1(int[] array){
	    int i,j;
	    int[] Lis = new int[array.length];
	    for(i=0;i<array.length;i++){
			Lis[i]=1;
	    	for(j=0;j<i;j++){
	    		if(Lis[j]+1>Lis[i]&&array[j]<array[i]){
	    			Lis[i]=Lis[j]+1;
	    		}
	    	}
	    }
	    return Max(Lis);
	}

3、0-1背包问题

即m(i, j)是背包容量为j, 可选物品为i,i+1, …, n 时问题最优解的代价.

伪代码：

For j=0 To min(wn-1, C) Do
m[n, j] = 0;
For j=wn To C Do
m[n, j] = vn;
For i=n-1 To 2 Do
   For j=0 To min(wi -1, C) Do
m[i, j] = m[i+1, j];
   For j=wi To C Do
    m[i, j]=max{m[i+1, j], m[i+1, j-wi]+vi};
If C<w1
Then m[1, C]=m[2, C];
Else m[1, C]=max{m[2, C], m[2, C-w1]+v1};