树状数组的理解

z3551906947

已于 2023-04-23 12:10:32 修改

阅读量50

点赞数

文章标签：算法 c语言数据结构

于 2023-04-19 16:31:34 首次发布

本文链接：https://blog.csdn.net/z3551906947/article/details/130226957

版权

1.树状数组

1.问题引入

1.问题

给出一个长度为n的数组，完成以下两种操作

1.将第x的数加上k

2.输出区间[x,y]内每个数的和

2.朴素算法：O（n^2)

1.单点修改O(1)

2.区间查询O(n^2)

3.树状数组：O(nlog(2)n)

1.单点修改：O(log(2)n)

2.区间查询：O(log(2)n)

2.树状数组引入分级管理制度

树状数组又被称为二进制所引树，通过二进制分解划分区间

1.区间长度

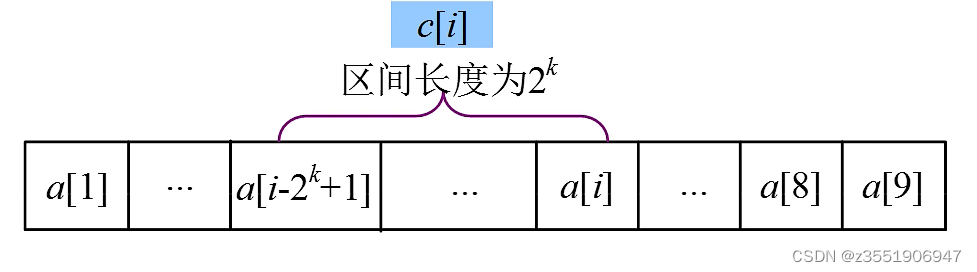
若i的二进制表示末尾有k个连续的0，则c[i]存储的区间长度为2^k，从a[i]向前数2^k个元素，

即c[i] = a[i - 2^k +1] + a[i- 2^k+2]+...+a[i]

计算区间长度

2.前驱和后继

直接前驱： c [ i ］的直接前驱为 c [ i - lowbit ( i )]，即 c [ i ］左侧紧邻的子树的根。

直接后继： c [ i ］的直接后继为 c [ i + lowbit ( i )]，即 c [ i ］的父节点。前驱： c [ i ］左侧所有子树的根。（计算前缀和）后继： c [ i ］的所有祖先。（更新点）

树状数组不能从0开始，如果从0开始，进行lowbit的操作，会进入死循环

例如：如果我们要计算sum[9]，那么只需要计算c[9] + c[8]

如果a[5]+10，那么只需要改变c[5],c[6]...

3.查询区间和

若要求值[i,j]，则求解前j个元素的和值减去前i-1个元素的和即可

即sum[j]-s[i-1]

4.算法实现

#include<stdio.h>
int max = 10005;
//定义数组和树状数组 
int n, a[10005] = {0}, c[10005] = {0};
//c[i]的区间长度
int lowbit(int i) { 
	return (-i) & i;
} 
//对点进行更新 
void add(int i, int z) {
	//更新所有的后后继 
	for(; i <= n; i += lowbit(i)) {
		c[i] += z;
	}
} 
//前缀和 
int sum(int i) {
	int s = 0;
	//累加所有的前驱 
	for(; i > 0; i -= lowbit(i)){
		s += c[i];
	}
	return s;
}
//区间和 
int  sum(int i, int j) {
	return sum(j) - sum(i - 1); 
}
int main() 
{
	scanf("%d", &n);
	for(int i = 1; i <= n; i++){
		scanf("%d", &a[i]);
		add(i, a[i]);//加入树状数组 
	}
	int x1, x2;
	scanf("%d", &x1);
	printf("%d\n",sum(x1));
	scanf("%d%d",&x1,&x2);
	printf("%d\n",sum(x1,x2));
	return 0; 
}

算法分析

点更新时，从叶子节点更新到树根，执行的次数不超过树的高度O(logn)。

前缀和查询时，从当前节点一直查询前驱，前驱的个数不超过O(logn)。

5.树状数组的局限性

2.例题

1626. 无矛盾的最佳球队 - 力扣（Leetcode）

1.思路

我们需要一个没有矛盾的团队，那么就是需要对年龄进行排序，然后利用树状数组，进行区间求和，后面就可以解决问题。

2.代码

#define MAX(a, b) ((a) > (b) ? (a) : (b))//用于判断两个值的大小
//二维数组调用快排
static int cmp(const void *pa, const void *pb) {
     //如果分数相同就按照年龄排序
    if (((int *)pa)[0] == ((int *)pb)[0]) {
        return ((int *)pa)[1] - ((int *)pb)[1];
    }
    return ((int *)pa)[0] - ((int *)pb)[0];
}
//树状数组得区间长度
int lowbit(int x) {
    return x & (-x);
}
//更新后继
void update(int i, int val, int *t, int max_age) {
    for (; i <= max_age; i += lowbit(i)) {
        t[i] = MAX(t[i], val);
    }
}
//前缀和
int query(int i, const int *t) {
    int ret = 0;
    for (; i > 0; i -= lowbit(i)) {
        ret = MAX(ret, t[i]);
    }
    return ret;
}

int bestTeamScore(int* scores, int scoresSize, int* ages, int agesSize) {
    int max_age = 0;
    //求出年龄最大
    for (int i = 0; i < agesSize; i++) {
        max_age = MAX(max_age, ages[i]);
    }
    //定义树状数组
    int t[max_age + 1];
    memset(t, 0, sizeof(t));
    int res = 0;
    //建立二维数组
    int people[scoresSize][2];
    int peopleSize = scoresSize;
    for (int i = 0; i < scoresSize; ++i) {
        people[i][0] = scores[i];
        people[i][1] = ages[i];
    }
    //进行排序
    qsort(people, peopleSize, sizeof(people[0]), cmp);
    //求出最大的无矛盾的
    for (int i = 0; i < peopleSize; ++i) {
        int score = people[i][0], age = people[i][1], cur = score + query(age, t);
        update(age, cur, t, max_age);
        res = MAX(res, cur);
    }
    return res;
}