Description
Assume the coasting is an infinite straight line. Land is in one side of coasting, sea in the other. Each small island is a point locating in the sea side. And any radar installation, locating on the coasting, can only cover d distance, so an island in the sea can be covered by a radius installation, if the distance between them is at most d.
We use Cartesian coordinate system, defining the coasting is the x-axis. The sea side is above x-axis, and the land side below. Given the position of each island in the sea, and given the distance of the coverage of the radar installation, your task is to write a program to find the minimal number of radar installations to cover all the islands. Note that the position of an island is represented by its x-y coordinates.
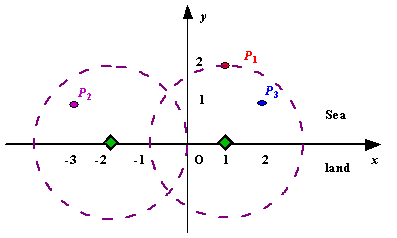
Figure A Sample Input of Radar Installations
We use Cartesian coordinate system, defining the coasting is the x-axis. The sea side is above x-axis, and the land side below. Given the position of each island in the sea, and given the distance of the coverage of the radar installation, your task is to write a program to find the minimal number of radar installations to cover all the islands. Note that the position of an island is represented by its x-y coordinates.

Figure A Sample Input of Radar Installations
Input
The input consists of several test cases. The first line of each case contains two integers n (1<=n<=1000) and d, where n is the number of islands in the sea and d is the distance of coverage of the radar installation. This is followed by n lines each containing two integers representing the coordinate of the position of each island. Then a blank line follows to separate the cases.
The input is terminated by a line containing pair of zeros
The input is terminated by a line containing pair of zeros
Output
For each test case output one line consisting of the test case number followed by the minimal number of radar installations needed. "-1" installation means no solution for that case.
Sample Input
3 2 1 2 -3 1 2 1 1 2 0 2 0 0
Sample Output
Case 1: 2 Case 2: 1
解题思路:
贪心算法,从左到右建立雷达,要尽量多地覆盖岛屿(对某一个岛屿而言,雷达建在能覆盖该岛屿的最右侧位置上)。
以岛屿为圆心,以d为半径画圆,如果画出的圆与x轴没有交点,则不能实现。存在交点的话,计算出第i个岛屿与x轴的交点坐标保存在结构体数组rad[i].sta与rad[i].end中。
对结构体数组排序,按照rad[i].end(因为确定雷达位置时依照end的值,保证将验证的未访问的点的end在当前end的右侧,若sta在当前sta的左侧,满足覆盖条件)进行升序排列。
然后一次从左到右找雷达。对于rad[i].end为当前最右边的左坐标,对于下一个岛屿,如果rad[j].sta<ran[i].end,则不需要建立新的雷达,需要更新下一个岛屿。否则需要建立新的雷达。
cpp源代码:
#include<iostream>
#include<math.h>
#include <stdio.h>
#include<algorithm>
#include<memory.h>
using namespace std;
const int Max = 1005;
struct
{
int x, y;
}isl[Max]; // 小岛的数据。
struct data
{
float sta, end;
}rad[Max]; // 小岛所对应雷达的数据。
bool cmp(data a, data b)
{
if(a.end < b.end)
return true;
else
return false;
}
int main()
{
int n, d, t = 1;
while(cin >> n >> d && n != 0)
{
int i, j, max_y = 0;
for(i = 0; i < n; i ++)
{
cin >> isl[i].x >> isl[i].y;
if(isl[i].y > max_y)
max_y = isl[i].y;
}
getchar();
getchar(); // PE了两次。
cout << "Case " << t ++ << ": ";
if(max_y > d || d < 0)
{
cout << -1 << endl;
continue;
}
float len;
for(i = 0; i < n; i ++)
{ // 求出小岛所对应雷达的可能覆盖范围。
len = sqrt(1.0 * d * d - isl[i].y * isl[i].y);
rad[i].sta = isl[i].x - len;
rad[i].end = isl[i].x + len;
}
sort(rad, rad + n, cmp); // 根据rad的end值进行排序。
int ans = 0;
bool vis[Max];
memset(vis, false, sizeof(vis));
for(i = 0; i < n; i ++)
{ // 类似的活动选择。
if(!vis[i])
{
vis[i] = true;
for(j = 0; j < n; j ++)
if(!vis[j] && rad[j].sta <= rad[i].end)
vis[j] = true;
ans ++;
}
}
cout << ans << endl;
}
return 0;
}






















 1108
1108

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








