Given a string S, find the longest palindromic substring in S. You may assume that the maximum length of S is 1000, and there exists one unique longest palindromic substring.
解:朴素的想法是以i为中心,不断向2边寻找回文,用数组P[i]记录长度最长的值,由于“aa”这样偶数个的回文串没有中心,我们先将原字符串补齐成“¥#a#a#”,再来进行统计,这样得到的P[i]有如下性质:
新串: # w # a # a # b # w # s # w # f # d #
辅助数组P: 1 2 1 2 3 2 1 2 1 2 1 4 1 2 1 2 1 2 1
P[i]记录的是以i为中心最长回文串在新字串向右延伸的位数(包括它自己!!),可以看到P[i]-1正好是此最长回文字符串在原字串中的长度。
这样的复杂度为O(n*n)。
Manacher方法O(n):
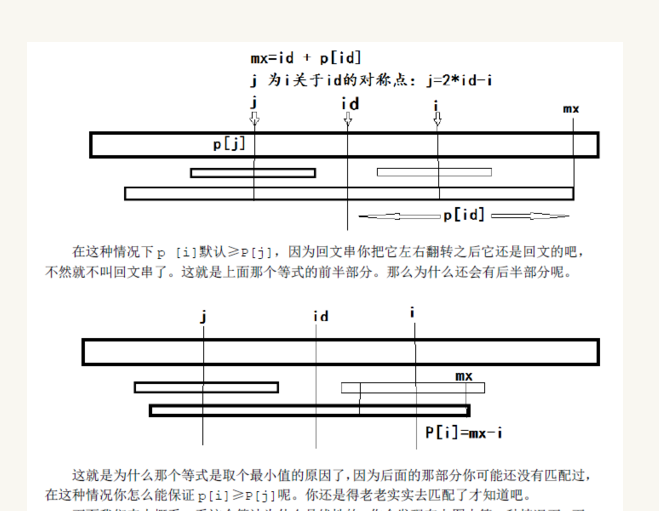
在上面的基础上利用到了回文字符串的性质,如下图:
计算P[i]的时候我们利用前面的已找到的信息,由于是回文串,那么前面的最长子串如果很长,假设是以id为中心,长度为P[id],那么对于i,其关于id对称点为j = 2 * id - i:
if id + P[id] > i:#如果当前中心在原来的子串范围内
P[id] = min(P[j],P[id] + id - i)#这里就是上图的2种情况
else:
P[id] = 0
#下面接着一个个挨着比较和第一种方法一样这算法是线性的原因是:我们可以看到仅当没有比较过的回文,我们才会继续下去比较,不然就包含在图中的情况中了,所以是线性的,仅比较未比较过的字符
class Solution(object):
def longestPalindrome(self, s):
"""
:type s: str
:rtype: str
"""
max = 0
PLen = [0]*3000
resCenter = 1
if len(s) == 0 | len(s) == 1:
return(s)
NewS = "$#"
for i in range(0,len(s)):
NewS += s[i]
NewS += '#'
for i in range(1,len(NewS)):
#j is the symmetry point of resCenter for i
j = 2 * resCenter - i
k = 0
#if max > i - resCenter:
# if max - i > p[j]:
# PLen[i] = PLen[j] 此时PLen[i]已经定型
# else:
# PLen[i] = max - i 此时PLen[i]还可以往后加
if max + resCenter > i:
PLen[i] = min(PLen[j],max + resCenter - i)
else:
PLen[i] = 0
#接下来就直接从k开始比较
k = PLen[i]
while (i - k >= 0) & (i + k < len(NewS)):
if NewS[i - k] == NewS[i + k]:
PLen[i] += 1
if max < PLen[i]:
max = PLen[i]
resCenter = i
k += 1
else:
break
max = int((max - 1)/2)
if NewS[resCenter] == '#':
resCenter = int(resCenter / 2 - 1)
return (s[resCenter - max + 1:resCenter + max + 1])
else:
resCenter = int(resCenter / 2 - 1)
return (s[resCenter - max:resCenter + max + 1])python 的a[m:n]是取的m 到 n - 1!






















 448
448

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








