题目链接:http://www.lydsy.com/JudgeOnline/problem.php?id=2301
【分析】
这题用的是莫比乌斯反演,于是乎蒟蒻去看PoPoQQQ大神的PPT学了一下莫比乌斯反演。
将问题转化为1<=x<=n,1<=y<=m且gcd(x,y)=k的数对个数,然后容斥一下。
设f(i)表示gcd(x,y)=i的数对个数,F(i)表示i|gcd(x,y)的数对个数,则有
然后就可以得到
由于[n/d]的取值只有2√n个(当d<=√n时[n/d]有√n个取值;当d>√n时[n/d]<=√n也只有√n个取值),于是可以将每次计算的复杂度降为√n。
时限是足够用的......
【代码】
#include <cstdio>
#include <algorithm>
using namespace std;
const int maxn=50010;
int Prime[maxn],NotPrime[maxn],mu[maxn],sum[maxn];
int a,b,c,d,k,T;
void Get_MU()
{
int cnt=0;
mu[1]=1;
for (int i=2;i<=maxn;i++)
{
if (!NotPrime[i]) {Prime[cnt++]=i;mu[i]=-1;}
for (int j=0;j<cnt && Prime[j]*i<=maxn;j++)
{
NotPrime[i*Prime[j]]=1;
if (i%Prime[j]==0) break;
mu[i*Prime[j]]=-mu[i];
}
}
for (int i=1;i<=maxn;i++) sum[i]=sum[i-1]+mu[i];
}
int Calc(int n,int m)
{
int ans=0,pos;
if (n>m) swap(n,m);
for (int i=1;i<=n;i=pos+1)
{
pos=min(n/(n/i),m/(m/i));
ans+=(sum[pos]-sum[i-1])*(n/i)*(m/i);
}
return ans;
}
int main()
{
Get_MU();
scanf("%d",&T);
while (T--)
{
scanf("%d%d%d%d%d",&a,&b,&c,&d,&k);a--;c--;
a/=k;b/=k;c/=k;d/=k;
printf("%d\n",Calc(b,d)+Calc(a,c)-Calc(a,d)-Calc(b,c));
}
return 0;
}









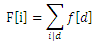















 145
145

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








