找寻链表中环的入口结点

题目描述

一个链表中包含环，请找出该链表的环的入口结点。

算法实现：

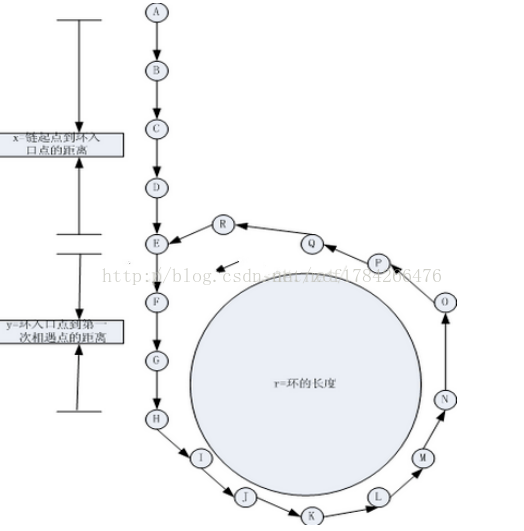
这个过程可以表示为下图：

（图片之前保存的，引用他人博客的，不过时间太久，找不到原出处了，原作者看到如果介意，可以告诉我）

如图中所示，设链起点到环入口点间的距离为x，

环入口点到问题1中fast与low重合点的距离为y，

步骤一：

设两个指针分别为fast和slow，（fast一次走2个结点，slow一次走一个结点），

又设在fast与low重合时fast已绕环n周（n>0），

则此时slow移动总长度为s,则fast移动总长度为2s，环的长度为r，

则：s+nr=2s，（fast移动长度2s等于slow移动的长度s，加上相遇时fast已经绕环走的距离，即n*r）

        s=x+y，（观察上图，slow移动长度就是起点到重合点的距离）

由s+nr=2s，得出s=nr，

再根据s=x+y，可得nr=x+y，则x=nr-y， 

步骤二：

然后再设一指针p1从起始位置开始遍历，p2从重合点开始遍历，二者每次都走一个结点，

根据上图，可知p1只需走x步，就会到达重合点，

此时p2也走了x步，根据步骤一的结论，可知x=nr-y，即p2走了（nr-y）步，

由于p2是在重合点开始遍历的，则最终位置=起始位置+走的步数，

根据上图，可得起始位置为（x+y），走的步数为（nr-y），

则最终位置=x+y+nr-y=x+nr，相当于到达x点处，再绕环n圈，最终点还是x点处，而x点就是环的入口点，

即，p1移动x步后第一次到达环的入口点时，p2也到达了环的入口点，

即p1与p2此时的相遇位置就是环的入口点的位置。

程序如下：

 public ListNode findNodeOfLoop(ListNode pHead)
    {
    	ListNode slow = pHead;
    	ListNode fast = pHead;	
    	while(slow!=null&&fast.next!=null){
    			slow=slow.next;
    			fast=fast.next.next;
    			if(slow==fast)
    				break;
    	}
    	if(fast==null||fast.next==null)
    		return null;

        //可以重置slow指针位置，指向开始位置，相当于步骤二中p1；
        //fast已经指在了重合位置，就相当于步骤二中的p2     

       slow = pHead;
    	while(slow!=fast){
    		slow=slow.next;
    		fast=fast.next;
    	}   	    	
		return slow;        
    }