数据结构与算法：Floyd最短路径算法

Floyd算法是一种多源最短路径算法，用于计算图中任意两个节点之间的最短路径。算法的基本思想是通过中间节点逐步优化路径长度，直到得到最短路径。

Floyd算法又称为插点法，是一种利用动态规划的思想寻找给定的加权图中多源点之间最短路径的算法，与Dijkstra算法类似。该算法名称以创始人之一、1978年图灵奖获得者、斯坦福大学计算机科学系教授罗伯特·弗洛伊德命名。

算法流程和步骤如下：

【1】 初始化一个二维矩阵dist，用于存储任意两个节点之间的最短路径长度。矩阵的大小为n x n，其中n为图中节点的个数。

【2】 将矩阵dist初始化为图中节点之间的直接距离，即如果存在一条从节点i到节点j的边，则dist[i][j]为边的权重，否则为一个很大的值（表示不存在直接路径）。

【3】 使用两个嵌套的循环，遍历所有的中间节点k，更新矩阵dist中任意两个节点之间的最短路径长度。

【4】 在循环中，对于任意的节点对(i, j)，如果存在一条从节点i经过节点k到节点j的路径，并且通过节点的路径长度小于当前的最短路径长度，则更新dist[i][j]为更短的路径长度。

【5】 重复步骤3和步骤4，直到遍历完所有的中间节点。

【6】 最后，矩阵dist中的元素就表示任意两个节点之间的最短路径长度。

下面举2个例子来描述算法步骤。

示例-1：

如下图所示。我们使用A0代表顶点i和j之间的直线距离，即A0为不经过任何顶点的矩阵；An代表i到j的最短距离。

步骤1：初始化矩阵，若没有路径则使用∞无穷大表示。

步骤2：找出A1[ I ][ j ]由i到j，经过顶点1的最短距离，并填入矩阵。

A1[1][2] = min{ A0 [1][2] , A0[1][1] + A0[1][2] }= min{ 4 ,0 + 4 } = 4

A1[1][3] = min{ A0 [1][3] , A0[1][1] + A0[1][3] }= min{11 ,0 + 11} = 11

A1[2][1] = min{ A0 [2][1] , A0[1][1] + A0[2][1] }= min{6 ,0 + 6} = 6

A1[2][3] = min{ A0 [2][3] , A0[2][1] + A0[1][3] }= min{2 ,6 + 11} = 2

A1[3][1] = min{ A0 [3][1] , A0[3][1] + A0[1][1] }= min{3 ,3 + 0} = 3

A1[3][2] = min{ A0 [3][2] , A0[3][1] + A0[1][2] }= min{∞ ,3 + 4} = 7

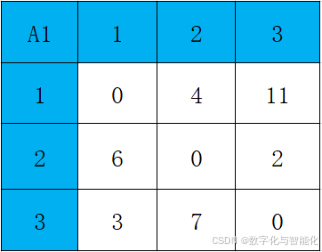
…(省略，自己试着写出全部结果) 按序求出各顶点的值后得到A1的矩阵为：