POJ 1177 Picture (线段树扫描线)

题意：

给定n个矩形（0 <= n < 5000）的左下角坐标(x1,y1)和右上角坐标(x2,y2)   (-10000 <= x1,x2,y1,y2 <= 10000)

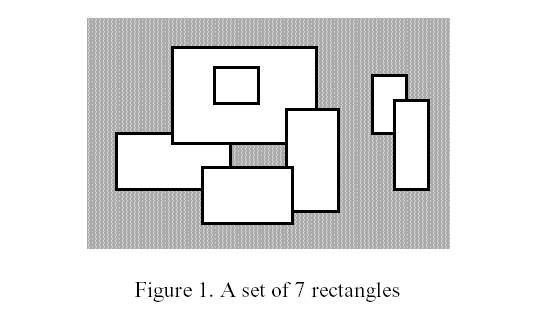
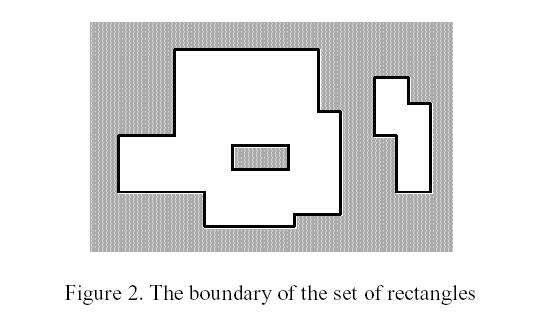
求所有矩形重合后的图形的周长，如下图（图片来自POJ 1177）：

做法：线段树扫描线。

由于值域不大，所以不需要离散化，直接将Y值向正方向平移10001个单位，然后用线段树直接做。

扫描线就是用垂直于x轴的线来从左到右扫描整个图形，然后用线段树来记录这条线上有多少个单位被覆盖。

struct Node{
int cover;//完全覆盖层数
int lines;//分成多少个线段
bool L,R;//左右端点是否被覆盖
int CoverLength;//覆盖长度 
int Length;//总长度 
};

为了计算与x轴平行的边，需要记录扫描线上有多少条线段，用lines 表示，然后 L,R表示该区间的左右端点是否被覆盖，方便合并区间的时候维护 lines。

Length是本区间的总长度，CoverLength是本区间被覆盖的长度，cover是指本区间被完全覆盖的次数，非完全覆盖不改变cover值。

然后，每个矩形，遇到左侧的边就将这条边加入扫描线，遇到右侧的边就把这条边从扫描线删除。

每次操作后更新周长。

具体见代码：

#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstring>
#include <algorithm>
#define  inf  0x1fffffff
#define out(i) <<#i<<"="<<(i)<<"  "
#define OUT1(a1) cout out(a1) <<endl
#define OUT2(a1,a2) cout out(a1) out(a2) <<endl
#define OUT3(a1,a2,a3) cout out(a1) out(a2) out(a3)<<endl
#define ls l,m,rt<<1
#define rs m+1,r,rt<<1|1
#define maxn 20007  //直接按y值建树 
using namespace std;

struct Node{
	int cover;//完全覆盖层数
	int lines;//分成多少个线段
	bool L,R;//左右端点是否被覆盖
	int CoverLength;//覆盖长度 
	int Length;//总长度 
	Node(){}
	Node(int cover,int lines,bool L,bool R,int CoverLength):cover(cover),lines(lines),L(L),R(R),CoverLength(CoverLength){}
	Node operator +(const Node &B){//连续区间的合并 
		Node C;
		C.cover=0;
		C.lines=lines+B.lines-(R&&B.L);
		C.CoverLength=CoverLength+B.CoverLength;
		C.L=L;C.R=B.R;
		C.Length=Length+B.Length;
		return C;
	}
	void Show(){
		printf("cover=%d  lines=%d  L=%d R=%d CoverLength=%d Length=%d\n",cover,lines,L,R,CoverLength,Length);
	}
}K[maxn<<2];
void PushUp(int rt){//更新非叶节点 
	if(K[rt].cover){
		K[rt].CoverLength=K[rt].Length;
		K[rt].L=K[rt].R=K[rt].lines=1;
	}
	else{
		K[rt]=K[rt<<1]+K[rt<<1|1];
	}
}
void Build(int l,int r,int rt){//建树 
	if(l==r){
		K[rt].L=K[rt].R=K[rt].cover=K[rt].lines=K[rt].CoverLength=0;
		K[rt].Length=1;
		return;
	}
	int m=(l+r)>>1;
	Build(ls);
	Build(rs);
	K[rt].cover=0;
	PushUp(rt);
}
void Cover(int L,int R,int l,int r,int rt){//覆盖 
	if(L <= l && r <= R){
		if(!K[rt].cover){//如果覆盖前为空，则更新节点内容 
			K[rt].L=K[rt].R=true;
			K[rt].lines=1;
			K[rt].CoverLength=K[rt].Length;	
		}
		K[rt].cover++;
		return;
	}
	int m=(l+r)>>1;
	if(L <= m) Cover(L,R,ls);
	if(R >  m) Cover(L,R,rs);
	PushUp(rt);
}
void Uncover(int L,int R,int l,int r,int rt){//移除覆盖 
	if(L <= l && r <= R){//如果移除后为空，则更新节点 
		--K[rt].cover;
		if(!K[rt].cover)  {
			if(l==r){//特判叶节点 
				K[rt].L=K[rt].R=K[rt].cover=K[rt].lines=K[rt].CoverLength=0;
			}
			else K[rt]=K[rt<<1]+K[rt<<1|1];//非叶节点用重载的+号 
		}
		return;
	}
	int m=(l+r)>>1;
	if(L <= m) Uncover(L,R,ls);
	if(R >  m) Uncover(L,R,rs);
	PushUp(rt);
}

int n;
struct Lines{//线段 
	int x,y1,y2,c;//x:线的横坐标  y1,y2：线的纵坐标端点  c:加入1  移除0 
	Lines(){}
	Lines(int x,int y1,int y2,int c):x(x),y1(y1),y2(y2),c(c){}
	bool operator < (const Lines &B)const{return x < B.x;} //重载小于号方便排序 
}L[10000];
int main(void)
{ 
	while(~scanf("%d",&n)){
		int x1,y1,x2,y2;
		for(int i=0;i<n;++i){
			scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
			L[i<<1]=Lines(x1,y1+10001,y2+10001,1);
			L[i<<1|1]=Lines(x2,y1+10001,y2+10001,0);
		}
		int nL=n<<1;
		sort(L,L+nL);//按x值排序 
		int PreX=L[0].x;//前X坐标 
		int ANS=0;//目前累计答案 
		int PreLength=0;//前线段总长
		int PreLines=0;//前线段数量 
		Build(1,20001,1);
		for(int i=0;i<nL;++i){
			//操作 
			if(L[i].c) Cover(L[i].y1,L[i].y2-1,1,20001,1);
			else Uncover(L[i].y1,L[i].y2-1,1,20001,1);
			//更新横向的边界 
			ANS+=2*PreLines*(L[i].x-PreX);
			PreLines=K[1].lines;
			PreX=L[i].x;
			//更新纵向边界 
			ANS+=abs(K[1].CoverLength-PreLength);
			PreLength=K[1].CoverLength;
		}
		//输出答案 
		printf("%d\n",ANS);
	}
return 0;
}