[AIZU ONLINE JUDGE] 计算几何 CGL_1

本文链接：https://blog.csdn.net/zeisenphael/article/details/140395855

Reflection（对称点）

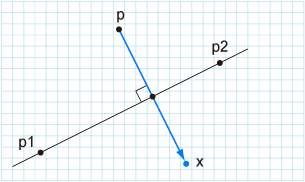
For given three points p1,p2,p, find the reflection point x of p onto p1p2.

Input

xp1 yp1 xp2 yp2
q
xp0 yp0
xp1 yp1
...
xpq−1 ypq−1

In the first line, integer coordinates of p1 and p2 are given. Then, q queries are given for integer coordinates of p.

Output

For each query, print the coordinate of the reflection point x. The output values should be in a decimal fraction with an error less than 0.00000001.

Constraints

1 ≤ q ≤ 1000
−10000 ≤ xi, yi ≤ 10000
p1 and p2 are not identical.

Sample Input 1

Sample Output 1

-1.0000000000 -1.0000000000
0.0000000000 -1.0000000000
1.0000000000 -1.0000000000

Sample Input 2

Sample Output 2

4.2400000000 3.3200000000
3.5600000000 2.0800000000
2.8800000000 0.8400000000

题目大意：

求出p关于直线 p1,p2 的对称点X;

题解：

对称点就是 P点 +（2倍垂足方向的向量）

所以问题就转化为了如何求解垂足

附上代码模板

#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>

using namespace std;

const double eps = 1e-10;

int sign(double x)
{
	if (fabs(x) < eps) return 0;
	else if (x > 0) return 1;
	return -1;
}

struct Point
{
	double x, y;

	Point(double x = 0, double y = 0) : x(x), y(y) { }

	Point operator + (const Point& t) { return Point(x + t.x, y + t.y); }
	Point operator - (const Point& t) { return Point(x - t.x, y - t.y); }
	Point operator * (const double t) { return Point(x * t, y * t); }
	Point operator / (const double t) { return Point(x / t, y / t); }
	bool operator == (const Point& t) { return !sign(fabs(x - t.x)) && !sign(fabs(y - t.y)); }
};

typedef Point Vector;

struct Line
{
	Point p;
	Vector v;

	Line(Point p, Vector v) : p(p), v(v) { }
};

int p;
Point A, B;

double dot(Vector A, Vector B)
{
	return A.x * B.x + A.y * B.y;
}

double norm(Vector A)
{
	return sqrt(dot(A, A));
}

//计算P到直线AB的垂足  // 比例
Point footpoint(Point A, Point B, Point P)
{
	Vector v1 = P - A, v2 = P - B, v3 = B - A;
	double len1 = dot(v1, v3) / norm(v3), len2 = -1.0 * dot(v2, v3) / norm(v3);
	return A + v3 * (len1 / (len1 + len2));
}

//计算点到直线的对称点
Point reflection(Point A, Point B, Point P)
{
	return P + (footpoint(A, B, P) - P) * 2;
}

int main()
{
	cin >> A.x >> A.y >> B.x >> B.y;
	cin >> p;

	while (p--)
	{
		Point C;
		cin >> C.x >> C.y;

		Point X = reflection(A, B, C);

		printf("%.10lf %.10lf\n", X.x, X.y);
	}


	return 0;
}