DP从玄学到科学—— 一招完全解决动态规划DP问题

先来一个有关动态规划的常规概念的描述

动态规划算法，又称DP算法，相信很多学习和打过算法赛的同学都知道，多多少少了解过。众所周知，dp算法的难度，在竞赛中通常为压轴题的难度，通常算法竞赛的难题，都多少涉及到动态规划（dp），这里就不作其他赘述。我相信，大家认同的观点都是：动态规划！难！

dp算法的本质是什么？作用是什么？

众所周知，dp算法，是用来简化和降低时间复杂度的！相比于普通的暴力枚举，暴力可能是指数级别的（O(2^n))，但是动态规划dp算法，可以简化时间复杂度，使其到O(n)级别 或者 O(n^2)级别，效率可以大大提高！从这个角度看，学好用好dp算法，是算法竞赛里面 很重要的一个部分！

dp算法正常教学模式的弊端

很多市面上的老师和课程，在讲授dp算法的时候，都会以所谓“老师”的角度来讲授和传达。何谓“老师”的角度呢？就是我知道答案了，然后反推过程来 为学生讲授解决dp问题。在我看来，这是不对的，是对于学生来讲不太负责任的行为。很容易想到，就是说我 拿到一道题目的时候，我是要从0开始去解决这个问题的，而不是知道100，然后去反推从0-100的过程。这是不恰当的。正确来讲，我们需要一个全新的，更好的方法，来帮助学生，真正的从学生的角度，去解决动态规划问题！！！！

我们将使用全新的方法去解决dp类问题

这是一个dp算法教学合集，简要介绍完dp的概念和现在教学的现状，我这次会使用一道例题（模板题）+一道变式题的模式，来为大家讲清楚怎么使用全新的方法去解决dp问题！！！

全新角度：以集合角度考虑DP问题

为什么dp算法能够简化时间复杂度？正是dp的本质：使用一个dp[i][j]来表示一类东西，简要来说，就是用一个数来表示一堆数（一类东西），所以它可以简化时间复杂度。

一道模板题《数字三角形》：

对于数字三角形，大家肯定在初学动态规划的时候，都会曾遇到，我下面将用新方法新角度来解决这个问题！！（大家看的时候，可能在这题上，会觉得我“宰鸡用牛刀”，但是这个方法是可以通过反复训练来不断熟练这个方法的，是对做下一道未知的题目有好处的。是站在学生视角来想这个问题的，而不是传统教学中的以“答案视角”解题，如果大家耐心看完，一定收获颇丰 ）

数字三角形

题目描述

题目相信大家都了解了，下面我将用新的方法解决这个问题：

第一步：写出状态表示：包含：集合定义 以及 集合属性

第二步：写出状态计算：包含：集合分类；得到状态转移方程

我们将数字三角形变成这个样子：就是向第一列对齐后！ 可以得到下面的结论：                       

我们接着往下分析：

给出完整的代码，我们再来探讨循环的问题：（100%通过率）

大家看这一行：

问题：大家有没有好奇过，为什么要从大到小循环呢，而不是从小到大循环？

图解：

这张图就已经说明的很清晰了；希望大家能够理解！！！

最后的求值要输出什么？f[1][1] ;   为什么？

一道衍生题《摘花生》：

同样的思路，大家来看看这个题目：

这个题目和《数字三角形》很相似，只是略有一点点变化

直接开始分析：

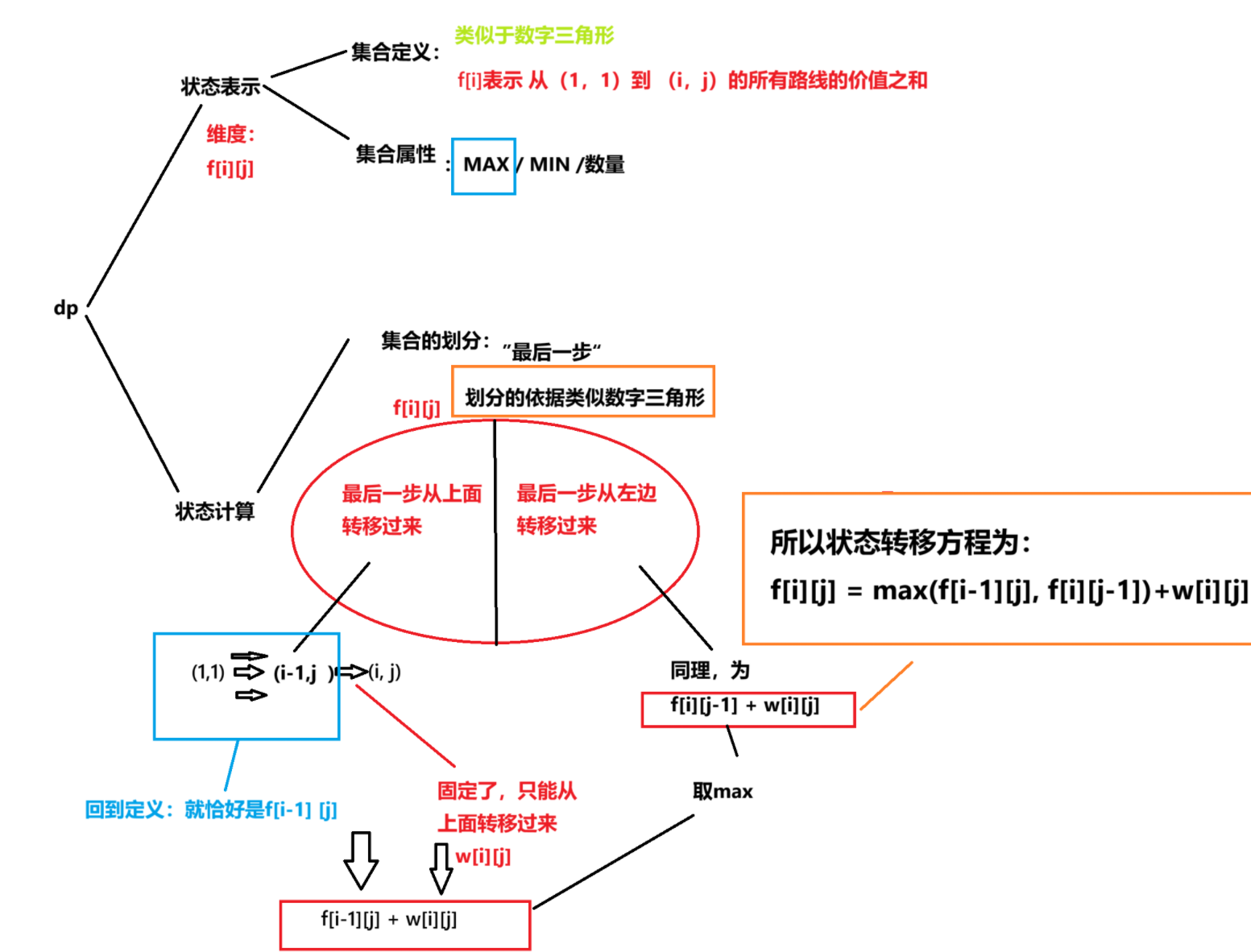
进行循环分析：

很自然的，就要初始化f[1][1]==1

而且很自然的，要得到f[n][n], 从下往上循环就可以（从小到大）

完整代码：

总结与注意：

我们的方法与传统的不一样

传统的状态转移方程的定义是：从（1.1）到（i. j）的价值 的最大值

但是我们 的方法有所差别：从（1.1）到（i. j）的所有路线的 价值 的最大值

别小看这四个字，正是它表现了我们的集合思想，使得逻辑更加好，紧密！！！

记住我们要时刻扣紧我们的集合定义，动态规划问题迎刃而解；

这其实才是一个比较简单的dp问题的解决方式，后续更新我会将很多复杂dp问题的解决方式用这个方法呈现出来，更有逻辑，更站在学生的角度！！！！

点个关注不迷路！谢谢大家的支持，如果你觉得我讲的好，请你为我点一个免费的 小心心和关注！！

感谢观看！

下期:  LIS模型