一、排序
排序就是给一堆无序的数字,排成从小到大或者从大到小的序列。
算法的稳定性:排序时候有一个问题,1,2,3,2这样的序列里面有两个2,如果按照某个算法排完序以后,这两个2依然是按照原来的顺序排列的,就说明这个算法是稳定的,否则是不稳定的。(后面所有算法都考虑到 稳定性这一因素,稳定性到底有什么用?)
1. 插入排序
1.1 直接插入排序
这就类似于我们在斗地主时候,输了很多把以后一般会蒙一把(所有牌都扣着,发完以后一把拿起,然后慢慢整理)这个时候,我们手牌上面,最左面一般是整理好的,右面是没有整理好的。。。。类似于之前在线性表中插入一个元素一样,首先我们找到待插入位置i,然后i后所有元素向后移一个位置,再进行插入。
所以,我们的插入排序一般就是三步,第一步,从后往前找到待插入的位子 第二步,把后面元素往后移,第三步,插!
这里我们把第一步和第二步一块做了。
int a[100];
void InsertSort(int n){
int i,j;
//刚开始输入序列是杂乱无章的
//a[0] = 0 也可以让a[0] =待排序的元素
for(j = 2;j<=n;j++){ //我们从第二个开始排序
//左面代表排好序了,右面是待排序的
int t = a[j];
//这里要强调一下for循环的执行步骤
//for(a;b;c)
//{
// d;
//}
//先1.a,2.b,
//然后 cbd 循环直到不满足b
for(i =j-1;t<a[i];i--){
a[i+1] = a[i];
}
a[i+1] = t;
}
}性质:
1.其是稳定的,因为我们在执行第一步时候,是从后往前找,其判断条件是 t<a[i],对于1 2 3 2 4 3 2。 判断2插入的位子时候,我们最后发现其插入的位子在2的后面,对于其他的2也是如此,因此排序以后,相同的元素最后相对位置是不变的。
2.空间复杂度是1(这里空间复杂度指的是额外开销的空间的大小)
3.最好情况下时间复杂度是O(n),最坏情况下是O(n*n),这里最好情况指的是待排序的序列和我们要求的顺序是一样的,比如都是从小到大,每一次我们都会跳出里面的for,所以最后复杂度是O(n)。而最坏情况恰好是两个相反,一个是从小到大,一个是从大到小。这就需要我们每一次都把一个元素移到头,每一次复杂度是n(执行步骤是 1,2,3,4,5,6,...n,平均是n/2),一共n次,所以总复杂度是O(n*n)。
1.2 折半排序
折半排序其实就是把查找那一部分优化了一下,原来相当于简单的查找,现在改成折半查找。但是整个查找的复杂度不会变。
int a[5] = {1,3,2,4,2};
int temp = -1;
int l,r,m;
for(int i = 1;i<5;i++){
l = 0;
r = i-1;
int temp = a[i];
while(l<=r){
m = (l+r)/2;
if(a[m]>a[i]){
r = m-1;
}
else {
l = m+1;
}
}
for(int j = i-1;j>=r;j--){
a[j+1] = a[j];
}
a[r+1] = temp;
}其复杂度计算方式为:n*(n*logn + n) = O(n*n),折半插入排序也是一个稳定的排序方法。但是折半查找只适用于线性表,因为他需要下标的相关计算。
1.3希尔排序
因为之前的排序复杂度都是n^2,对于数据量很大时候并不适用。因此,希尔提出了一种叫希尔排序的方法。具体实现方法书上有,这里举一个栗子:
给出关键字序列{50,26, 38, 80, 70, 90, 8, 30, 40, 20}的希尔排序过程(取增量序列为d = {5,3,1},排序结果为从小到大排列)。
第一趟,当d = 5时,其意思就是从第1个数字50开始,把与其间隔为5的数字取出来(90),进行插入排序。然后从第二个数字开始,也进行上述操作。直到第5个数字结束。也就是其集合划分为:
{50,26, 38, 80, 70, 90, 8, 30, 40, 20}
相同颜色为一个集合,集合内部进行插入排序,不同颜色外部的顺序是不变的,结果为:
{50,8, 30, 40, 20, 90, 26, 38, 80, 70}
第二趟(d = 3),先进行集合的划分:
{50,8, 30, 40, 20, 90, 26, 38, 80, 70}
划分后,相同颜色进行插入排序:
{26,8, 30, 40, 20, 80, 50, 38, 90, 70}
第三趟(d = 1),先进行集合的划分:
{26,8, 30, 40, 20, 80, 50, 38, 90, 70}
划分后,相同颜色进行插入排序:
{8,20, 26, 30, 38, 40, 50, 70, 80, 90}
希尔排序的空间复杂度是O(1),时间复杂度是O(n^1.3)。只适用于线性表。并且其排序是不稳定的。
2.交换排序
2.1 冒泡排序
对于从小到大排序,冒泡排序相当于每次选出一个最大的放在最右面。下一次排序中,之前选出来的最大元素不再参与比较,我们只是把剩下的元素中,选出一个最大的,放在最右面(之前选出来的元素的最左面)。
int a[5] = {1,3,2,4,2};
int temp = -1;
int l,r,m;
for(int i = 0;i<5;i++){
for(int j = 0;j<5-i+1;j++){
if(a[j]>a[j+1]){
int temp = a[j];
a[j]= a[j+1];
a[j+1] = temp;
}
}
}空间复杂度是O(1),时间复杂度是O(n*n)。其是稳定的排序。
2.2 快速排序
利用分治的思想,每一次在集合中随机的选取一个元素pivot(一般选择第一个元素)为基准,把所有小于pivot放在pivot的左边集合left,把所有大于等于pivot的元素放在pivot的右边集合right。然后对于left以及right利用相同的方法进行快排处理。
int Partition(int *A, int low, int high){
int pivot = A[low];
while(low < high){
//1. 从右面找到第一个比pivot小的元素
while(low < high && A[high] >= pivot) high--;
A[low] = A[high];
//2. 从左面找到第一个比pivot大的元素
while(low < high && A[low] <= pivot) low++;
A[high] = A[low];
}
//3.将pivot进行赋值
A[low] = pivot;
return low;
}
int stable_Partition(int *A, int low, int high){
vector<int> lower;
vector<int> higher;
int pivot = A[low];
for(int i = low+1;i<high;i++){
if(A[i]<pivot) lower.push_back(A[i]);
else higher.push_back(A[i]);
}
int k = low;
for(int i=0;i<lower.size();i++){
A[k++] = lower[i];
}
A[k++] = pivot;
for(int i = 0;i<higher.size();i++){
A[k++] = higher[i];
}
return low;
}
void QuickSort(int *A, int low, int high){
if(low < high){
int pivotpos = stable_Partition(A, low, high);
QuickSort(A, low, pivotpos-1);
QuickSort(A, pivotpos+1, high);
}
}其空间复杂度为O(log(n)),时间复杂度为O(nlog(n)),其并不是稳定的排序。举个栗子:{3,2,2},对于快速排序来说,最开始low=0,high = 2,我们先选取第一个元素3作为基准,把小于3的元素放在左面,大于等于3的元素放在右面。
如代码Partition(int *A, int low, int high)函数所示,首先执行第一步,我们是从最右面开始,也就是第一次遇到的是2,把它放在low的位置上(这时候low = 0,high = 2):{2,2,2}。
然后执行第二步,找一个比3大的元素放在3的右面,因为前两个{2,2}满足循环,所以low=2,对于第三个2,这时候low=high,不满足第一个条件,跳出。
执行第三步,A[low= 2] = 3,所以最后排序结果为{2,2,3},可以看到两个2的顺序反了,所以其不满足稳定性。
当元素随机的时候,快排的效率最高,因为在快排中,需要将集合划分为两个区间,如果两个区间中的元素个数趋于一致时候,快排的效果最好(这样会使的递归的深度最小)。如果元素基本有序时候,会使得左右两个区间元素个数严重不平衡,比如{1,2,3}。第一趟快排中,左区间的元素个数为0,右区间的个数为2。
举个快排的栗子:
{25,84,21,47,15,27,68,35,20}
第一趟排序结果为:
{20,15,21,25,47,27,68,35,84}
第二趟排序结果为:
{15,20,21,25,35,27,47,68,84}
第三趟排序结果为:
{15,20,21,25,27,35,47,68,84}
快排中,并不是一股脑的把比第一个元素小的放在左面,把比第一个元素大的放在右面,比第一个元素小的元素放在左面中,其也有一定的顺序,同理右面的也有一定的顺序。顺序不能乱,严格按照代码中,先从high开始向左走,选择第一个小的元素放在low位置上,然后从low开始向又走,选择第一个大的元素放在high上,如此反复直到low=high(也就是其不满足条件 low<high)。
那么,上述例子中,采用直接插入排序(折半排序只不过是查找的过程不一样,其集合中元素变化过程和直接插入排序是一致的),希尔排序(步长为5,3,1),冒泡排序的过程是什么样的呢?
3.选择排序
3.1 简单选择排序
假定排序表为L[1...n],第i趟排序即从L[i..n]中选择一个最小的元素与L[i]进行交换,这样每次我们就可以确定一个元素的位置(希尔排序每次可不可以确定一个元素的位置?,其他排序算法呢)。这样经过n-1趟排序就可以确定整个序列的顺序。其空间复杂度为O(1),时间复杂度为O(n^2),并且简单选择排序是不稳定的(其与冒泡排序的思想都是每次在剩下的集合中选出一个最大/最小的元素放在有序集合的后面,但是冒泡是有序的,简单选择排序是不稳定的,为什么?)。
3.2 堆排序
堆排序有两种,一种是小顶堆,一种是大顶堆。小顶堆中父节点小于等于两个孩子结点,大顶堆中父节点大于等于两个孩子结点。堆排序中核心考点是堆的建立、插入、删除。
在建立过程中,先将给定序列转化为二叉树,然后从第一个有叶节点的结点开始(n/2取下界),对于小顶堆,如果子节点中最大的结点比父节点大,那么两个进行交换(下沉)。注意在交换完以后,原来的父节点可能还会比新位置上的两个子节点小,这时候我们还需要进行下沉操作。
在插入过程中,先将待插入的结点放在最后一位,然后通过与父节点进行比较,不断进行上浮操作。
在的删除过程中,我们只能删除根节点,首先需要将根节点与最后一个结点进行交换,然后对于变为新根节点的那个原来的最后一个结点,我们需要不断的进行下浮操作。
举个栗子:利用堆排序建立小顶堆:{15,9,7,8,20,-1,7,4}。然后插入3(插入3后一共需要比较几次),然后删除一个元素。
4.归并排序和基数排序
4.1 归并排序
归并排序可以从上往下排序,也可以从下往上,这里我们主要研究的是从下网上排序,也就是对于n个元素,我们先将每一个元素看成一个独立的集合,首先,相邻的两个组合为一个集合,内部进行排序。然后新的集合再两两合并,直到最后只有一个集合。
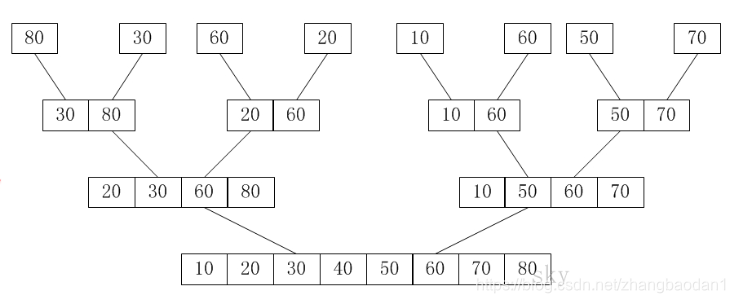
其空间复杂度是O(n),时间复杂度是O(nlogn),其实稳定的排序算法。
4.2 基数排序
这个排序算法比较奇特,是按照数字的个位排序完以后,再排十位,直到所有位置排完为止。举个栗子:
{100,119,007,911,114,120,122}
第一趟排序完以后:
{100,120,911,114,122,007,119}
第二趟排序完以后:
{100,007,911,114,119,120,122}
第三趟排序完以后:
{007,100,114,119,120,122,911}

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








