算法分析（二）

算法分析

前言：开始对自己的学习做一个记录，看看自己的知识图谱是什么样子。如果可以帮助到其他人是也是一件非常开心的事，更多的是对学习的东西的一个整理。

学习地址：网易公开课的算法导论。链接：
http://open.163.com/special/opencourse/algorithms.html

---

Divde the Conquer(分治法)

1.Divide the problem into the one more subproblems

2.Conquer:each subproblem recursion

3.combine:solutions

注：分治法基本思路是把大问题分解成小问题,通过递归方式把小问题再度分解到可以解决程度，通过合并来完成问题的求解。递归是分治法中解决问题的方式并不等同于分治法。递归是 通过 for 改写。

---

Some problems are solved by Divde the Conquer.

Binary search(二分查找)

1.Divide：compore x with middle
2.Conquer：recurse x on sub array
3.combin : trival
T(n) = T(n/2) + θ(1) = θ(lgn)

Marge Sort(归并)

1.Divide：divided your array into two halves
2.Conquer：recursively sort each subarray
3.combin : linear time merge
T(n) = 2T(n/2) + θ(n) = θ(nlgn)

Powering number(乘方问题)

Give you a number x（int,double,float…） and give you a integer n (n>0),comput x^n

solve 1 ：
x·x·x····x = x^n

solve 2 ：

$$x^n = \begin{cases} x^{n/2}·x^{n/2}&\text{$n$ 为偶数},\\ x^{(n-1)/2}·x^{(n-1)/2}·x&\text{$n$ 为奇数}. \end{cases}$$
T(n) = T(n/2) + θ(1) = θ(lgn)

Fibonaci numbers(斐波那契数)

solve 1 ： navie recursive squaring(朴素平方递归式)

$$F_n = \begin{cases} 0&\text{$n=0$},\\ 1&\text{$n=1$},\\ F_{n-1} + F_{n-2} &\text{$n>=2$}. \end{cases}$$

T(n) = Ω(Φ^n) Φ =(1+√5)/2

solve2：bottom-up algorithms(自下而上计算)

注：通过自下而上计算来减少F(n-2)重复的部分

Compute F0,F1,F2,……,Fn

T(n) = θ(n)

solve3：not allowed
Fn = （Φ^n）/√5 round it to the nearest integer that is the nth Fibonacci number Φ =(1+√5)/2
注：这个方法是通过 Fibonaci numbers 的数学特性获取,当n取特别大时候，浮点数精度会影响结果。

solve4：squaring algorithmn(平方递归算法)

$$\left\{ {\begin{array}{*{20}c} F_{n+1} & F_{n} \\ F_{n} & F_{n-1} \\ \end{array}} \right\} = \left\{ {\begin{array}{*{20}c} 1 & 1 \\ 1 & 0 \\ \end{array}} \right\}^n$$
注：斐波那契数可由上述矩阵函数表示

证明如下：
假设 n=1 ，即

$$\left\{ {\begin{array}{*{20}c} F_{2} & F_{1} \\ F_{1} & F_{0} \\ \end{array}} \right\} = \left\{ {\begin{array}{*{20}c} 1 & 1 \\ 1 & 0 \\ \end{array}} \right\}^1 = \left\{ {\begin{array}{*{20}c} 1 & 1 \\ 1 & 0 \\ \end{array}} \right\}$$
设 当 n>2 时,即
$$\left\{ {\begin{array}{*{20}c} F_{n} & F_{n-1} \\ F_{n-1} & F_{n-2} \\ \end{array}} \right\} = \left\{ {\begin{array}{*{20}c} 1 & 1 \\ 1 & 0 \\ \end{array}} \right\}^{n-1} \\ \left\{ {\begin{array}{*{20}c} F_{n} & F_{n-1} \\ F_{n-1} & F_{n-2} \\ \end{array}} \right\} \left\{ {\begin{array}{*{20}c} 1 & 1 \\ 1 & 0 \\ \end{array}} \right\}= \left\{ {\begin{array}{*{20}c} 1 & 1 \\ 1 & 0 \\ \end{array}} \right\}^{n-1} \left\{ {\begin{array}{*{20}c} 1 & 1 \\ 1 & 0 \\ \end{array}} \right\} \\ \left\{ {\begin{array}{*{20}c} F_{n}+F_{n-1} & F_{n} \\ F_{n-1}+F_{n-2} & F_{n-1} \\ \end{array}} \right\}= \left\{ {\begin{array}{*{20}c} 1 & 1 \\ 1 & 0 \\ \end{array}} \right\}^{n}\\ \left\{ {\begin{array}{*{20}c} F_{n} & F_{n-1} \\ F_{n-1} & F_{n-2} \\ \end{array}} \right\}= \left\{ {\begin{array}{*{20}c} 1 & 1 \\ 1 & 0 \\ \end{array}} \right\}^{n}$$

Matrix multiplications(矩阵乘法)
Input A[aij]，B[bij] i,j = 1,2,3,4….mn
Output C=[cij]=AB

$$C_{ij}=\sum_{k=1}^{n} a_{ik}b_{kj} = 0$$

//pseudocode伪代码
    for i<-1 to n
        do for j<-1 to n
            c_{ij}<-0
            do for k<- to n
                Cij<-Cij +aik·bki

可以通过矩阵切割实现
Idea ： n*n matrix = 2*2 block matrix of n/2 * n/2 of matrix

$$\left\{ {\begin{array}{*{20}c} r & s \\ t & v \\ \end{array}} \right\} = \left\{ {\begin{array}{*{20}c} a & b \\ c & d \\ \end{array}} \right\} \left\{ {\begin{array}{*{20}c} e & f \\ g & h \\ \end{array}} \right\}$$

r = ae + bg
s = af + bh
t = ce + gd
v = cf + dh

8 recvrsive multiplication of n/2-by-n/2 matrixex
4 addtions -> θ(n^2)
T(n) = 8T(n/x) + θ(n^2) = θ(n^3)

Strassen’s algorithm
Strassen算法可以相比矩阵运算，减少一次乘法运算
P1=a(f-h)
P2=(a+b)h
P3=(c+d)e
P4=d(g-e)
P5=(a+d)(e+h)
P6=(b-d)(g+h)
P7=(a-c)(e+f)

r=P5+P4-P2+P6
s=P1+P2
t=P3+P4
u=P5+P1-P3-P7

1.Divide A,B compcte terms for producfs θ(n^2)
2.Confuer recursively computing all the P1….P7
3.Combine r,a,t,v
T(n)=7T(n/2)+θ(n^2)=θ(nlg7)=O(n^2.81)

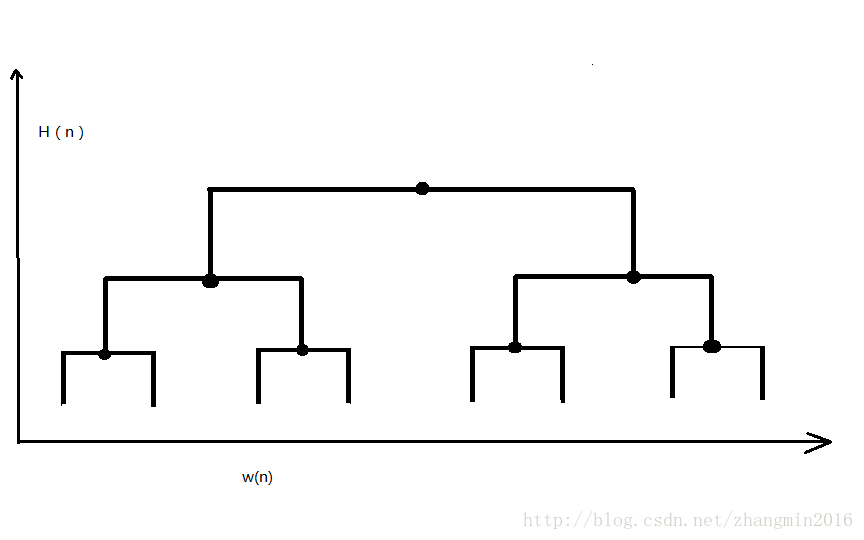
VLSI Layout(集成电路问题)

Problem Embed complete binary tree on n leaves in a gird with minmum area

Naive embedding

H(n)=H(n/2)+1=θ(lgn)
W(n)=2W(n/2)+1=θ(n)
Area=θ(nlgn)

Gool:想要实现Area=θ(n) 即猜想:
H(n)=θ(√n)
W(n)=θ(√n)
则T(n)=2T(n/4)+θ(n^(1/2-e))
图为:

L(n)=2L(n/4)+θ(1)=θ(√n)

注：

$$aT(n/b)=θ(log_nb)$$